![]()
what makes me confident
of what I say?
S OURCES AND A BBREVIATIONS
Sources cited in these notes are listed in the bibliography.
Abbreviations used in these notes are:
ECP-1—The Collected Papers of Albert Einstein, Volume 1, cited in bibliography as ECP-1.
ECP-2—The Collected Papers of Albert Einstein, Volume 2, cited in bibliography as ECP-2.
INT—Interviews by the author, listed at beginning of bibliography.
MTW—Misner, Thorne, and Wheeler (1973).
P ROLOGUE
Page
| 23 | [Of all the conceptions . . . finding them.] This paragraph is adapted from Thorne (1974). |
| 26 | [From the orbital period . . . (“10 solar masses”).] Newton’s formula is M h = C o 3 / (2π GP o 2 ) , where M h is the mass of the hole (or any other gravitating body), C o and P o are the circumference and period of any circular orbit around the hole, π is 3.14159 . . . , and G is Newton’s gravitation constant, 1.327 × 10 11 kilometers 3 per second 2 per solar mass. See note to page 61, below. Inserting into this formula the starship’s orbital period P o = 5 minutes 46 seconds, and its orbital circumference C o = 10 6 kilometers, one obtains a mass M h = 10 solar masses. (One solar mass is 1.989 × 10 30 kilograms.) |
| 28 |
[As for size,. . . Sun’s mass.] The formula for the horizon circumference is C
h
= 4π
GM
h
/c
2
= 18.5 kilometers × (
M
h
/M
|
| 35 | [In honor of those tides, . . . tidal force.] The tidal force, expressed as a relative acceleration between your head and feet (or between any other two objects), is Δ a = 16π 3 G ( M h / C 3 ) L , where G is Newton’s gravitation constant (see above), M h is the black-hole mass, C is the circumference at which you are located, and L is the distance between your head and feet. Note that 1 Earth gravity is 9.81 meters per second 2 . See, e.g., page 29 of MTW. |
| 37 | [General relativity predicts, . . . actually decreases.] The above formula (note to page 35) gives for the tidal force Δ a ∝ M h / C 3 . When the circumference is nearly that of the horizon, C ∝ M h (note to page 28), so Δ a ∝1/ M h 2 . |
| 37 | [The entire trip of 30, 100 light-years . . . only 20 years.] Starship time T ship , Earth time T E , and distance D traveled are related by T E = (2 c / g )sinh( gT ship /2 c ) and D = (2 c 2 / g )[cosh( gT ship /2 c ) – 1], where g is the ship’s acceleration (“one Earth gravity,” 9.81 meters per second 2 ), c is the speed of light, and cosh and sinh are the hyperbolic cosine and hyperbolic sine functions. See, e.g., Chapter 6 of MTW. For trips that last much more than one year, these formulas become, approximately, T E = D / c and T ship = (2 c / g )ln( gD / c 2 ), where In is the natural logarithm. |
| 39 | [To remain in a circular orbit, . . . hurled you inward.] For a mathematical analysis of circular (and other) orbits around a nonspinning black hole, see, e.g., Chapter 25 of MTW, and especially Box 25.6. |
| 40 |
[Your calculations show . . . 1.0001 horizon circumferences.] The acceleration force you will feel, hovering at a circumference
C
above a black hole of mass M
h
and horizon circumference
C
h
, is
a
= 4π
2
G
(
M
h
/0) × (1/
|
| 40 | [Using the usual 1 -g acceleration . . . crew in the starship.] See the second note for page 37 above. |
| 43 |
[The spot is small . . . seen from Earth.] When one hovers at a circumference
C
slightly above a horizon with circumference
C
h
one sees all the light from the external Universe concentrated in a bright disk with angular diameter
|
| 44 |
[Equally peculiar, the colors . . . 5 × 10
-7
meter light.] When one hovers at a circumference
C
slightly above a horizon with circumference
C
h
, one sees the wavelengths l of all light from the external Universe gravitationally blue-shifted (the inverse of the gravitational redshift) by λ
received
/λ
emitted
=
|
| 49 |
[
Inserting these numbers . . . coalesce seven days from now.] When two black holes, each with mass
M
h
, orbit each other with separation
D
, they have an orbital period
|
| 53 | [The ring has a circumference of 5 million kilometers, . . . curvature of spacetime.] A person on the girder-work ring at a distance L from its central layer feels an acceleration a = (24π 3 GM h / C 3 ) L toward the central layer, caused one third by the rotating ring’s centrifugal force and two thirds by the hole’s tidal force. G is Newton’s gravitation constant, M h is the hole’s mass, and C is the circumference of the ring’s central layer. For comparison, 1 Earth gravity of acceleration is 9.81 meters per second 2 . See the note for page 35 above. |
| 55 |
[The laws of quantum gravity . . . usable for time travel.] 1.62 × 10
-33
centimeter =
|
| 57 – 58 | [Another is the fact that, . . . flying colors.] See, e.g., Will (1986). |
C HAPTER 1
| 59 | General comment about Chapter 1: Most of this chapter’s material about Einstein’s life comes from the standard biographies of him: Pais (1982), Hoffman (1972), Clark (1971), Einstein (1949), and Frank (1947). For most of the historical perspective and quotations in Chapter 1, which I have gleaned from these standard biographies, I do not give individual citations below. Much new historical material is becoming available with the gradual publication of Einstein’s collected papers, ECP-l, ECP-2, and Einstein and Maric (1992). I do cite, below, material from these sources. |
| 59 – 60 | [Professor Wilhelm Ostwald . . . Hermann Einstein.] Document 99 in ECP-1. |
| 60 | [“Unthinking respect . . . enemy of truth,”] Document 115 of ECP-l, as translated on page xix of Renn and Schulmann (1992). |
| 61 | Footnote 1: The following example illustrates what is meant by “mathematically manipulating” the laws of physics. |
| Early in the seventeenth century, Johannes Kepler deduced, from Tycho Brahe’s observations of the planets, that the cube of the circumference C of a planet’s orbit divided by the square of its orbital period P , i.e., C 3 /P 2 , was the same for all the planets then known: Mercury, Venus, Earth, Mars, Jupiter, Saturn. A half century later, Isaac Newton explained Kepler’s discovery by a mathematical manipulation of the Newtonian laws of motion and gravity (the laws listed on page 61 of the text): |
1. From the following diagram and a fair amount of sweat, one deduces that, as a planet encircles the Sun, the planet’s velocity changes at a rate given by the formula, (rate of change of velocity) = 2π C / P 2 , where π = 3.14159. . . . This rate of change of velocity is sometimes called the centrifugal acceleration that the orbiting planet experiences.
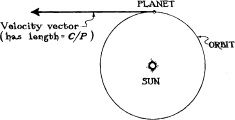
2. Newton’s second law of motion tells us that this rate of change of velocity (centrifugal acceleration) must be equal to the gravitational force, F grav exerted by the Sun on the planet, divided by the planet’s mass, M planet ; In other words, 2π C / P 2 = F grav / M planet .
3. Newton’s gravitational law tells us that the gravitational force F grav is proportional to the Sun’s mass M Sun times the planet’s mass M planet divided by the square of the planet’s orbital circumference. Stated as an equality rather than a proportionality, F grav = 4π 2 GM Sun M planet / C 2 . Here G is Newton’s constant of gravitation, equal to 6.670 × 10 -20 kilometer 3 per second 2 per kilogram, or equivalently 1.327 × 10 11 kilometers 3 per second 2 per solar mass.
4. By inserting this expression for the gravitational force F grav into Newton’s second law of motion (Step 2 above), we obtain 2π C/P 2 = 4π 2 GM Sun / C 2 . By then multiplying both sides of this equation by C 2 /2π, we obtain C 3 / P 2 = 2π GM Sun .
| Thus, Newton’s laws of motion and gravity explain—in fact they enforce—the relationship discovered by Kepler: C 3 /P 2 is the same for all planets; it depends only on Newton’s gravitation constant and the Sun’s mass. | |
| As an illustration of the power of the laws of physics, the above manipulations not only explain Kepler’s discovery, they also offer us a method to weigh the Sun. By dividing the final equation in Step 4 by 2π G , we obtain an equation for the Sun’s mass, M Sun = C 3 / (2π GP 2 ). By inserting into this equation the circumference C and period P of any planet’s orbit as measured by astronomers and the value of Newton’s gravitation constant G as measured in Earth-bound laboratories by physicists, we infer that the mass of the Sun is 1.989 × 10 30 kilograms. | |
| 62 |
[“Weber lectured . . . his every class.”] Document 39 in ECP-1; Document 2 in Einstein and Mari
|
| 63 | [And since the aether . . . at rest in absolute space,] In this chapter, I ignore the speculations by some physicists in the late nineteenth century that in the vicinity of the Earth the aether might be dragged along by the motion of the Earth through absolute space. There in fact was strong experimental evidence against such dragging: If, near the Earth’s surface, the aether was at rest with respect to the Earth, then there should be no aberration of starlight; but aberration due to the Earth’s motion around the Sun was a well-established fact. For a brief discussion of the history of ideas about the aether, see Chapter 6 of Pais (1982); for more detailed discussions, see references cited therein. |
| 64 | [Albert Michelson . . . had invented.] The technology of Michelson’s time was not capable of comparing one-way light speeds in various directions with sufficient accuracy (1 part in 10 4 ) to test the Newtonian prediction. However, there was a similar prediction of a difference in round-trip light speeds (about 5 parts in 10 9 difference between a round-trip parallel to the Earth’s motion through the aether and one perpendicular). Michelson’s new technique was ideally suited to measuring such round-trip differences; they were what Michelson searched for and could not find. |
| 65 | [By contrast, Heinrich Weber . . . mislead young minds.] I do not know for certain that Weber was confident of this, or that he in particular took the attitude that it would be inappropriate to mention the Michelson–Morley experiment in his lectures. This passage is speculation based on the absence of any sign that Weber discussed the experiment, or the issues raised by the experiment, in his lectures; see the detailed notes on his lectures taken by Einstein (Document 37 in ECP-1) and the brief description (page 62 of ECP-1) of the only other existing set of notes from Weber’s lectures. |
| 65 | [By comparing it with other experiments,] The other experiments were those, such as measurements of the aberration of starlight, which implied that the aether is not dragged along by the Earth; see note to page 63, above. |
| 65 | [A tiny (five parts in a billion) . . . Michelson–Morley experiment.] Recall (note to page 64) that Michelson was actually measuring round-trip light speeds and looking for variations with direction of about five parts in a billion. |
| 66 | [If one expressed . . . (see Figure 1.1c).] This discussion of the “no ends on magnetic field lines” law, and the more detailed discussion in Figure 1.1, is my own translation, into modern pictorial language, of one aspect of the Maxwell’s equations issue with which Lorentz, Larmor, and Poincaré struggled. For a more precise discussion of this issue and their struggle, see pages 123–130 of Pais (1982). |
| 66 | [If the Fitzgerald contraction . . . “dilates” time.] To make the laws beautiful required not only the contraction of moving objects and the dilation of their time, it also required pretending that the concept of simultaneity is relative, i.e., that simultaneity depends on one’s state of motion; and Lorentz, Larmor, and Poincaré paid considerable attention to this as well as to length contraction and time dilation. However, for pedagogical simplicity, I ignore this in the text and take up the issue of simultaneity somewhat later in Chapter 1. |
| 68 | [“I am more and more convinced . . . not correct.”] Document 52 in ECP-1; Document 8 in Einstein and Marić (1992). |
| 68 | [Over the next six years, . . . dilation of time.] Here I am speculating. It is not really known to what extent Einstein’s mind focused on these issues during 1899–1905. As Pais (1982, Section 6b) makes clear, during these six years Einstein was unaware of the Lorentz–Poincaré–Larmor deduction of length contraction and time dilation from Maxwell’s laws. Stated more technically, he was aware of Lorentz’s derivation of the Lorentz transformation up to first order in velocity (including simultaneity breakdown), but not to second order where length contraction and time dilation occur. On the other hand, he presumably was aware of the Fitzgerald–Lorentz inference of length contraction from the Michelson–Morley experiment; and we do know that in his 1905 paper on special relativity he gives his own derivation of the full Lorentz transformation, accurate to all orders, and of length contraction, time dilation, and simultaneity breakdown. |
| 69 | [To the saucy . . . Mileva Marić,] For a description of Marić’s personality based largely on the love letters between her and Einstein, see Renn and Schulmann (1992); for the love letters see ECP-1 or Einstein and Marić (1992). |
| 69 | [“I’m absolutely convinced . . . bad recommendation.”] Document 94 of ECP-1; Document 95 of Einstein and Maric (1992). |
| 69 | [“I could have found . . . thick hide.”] Document 100 of ECP-1. |
| 69 | [“This Miss Marić . . . dislike her.”] Document 138 of ECP-1. |
| 69 | [“That lady seems . . . wicked people!”] Document 125 of ECP-1. |
| 69 | [“I am beside myself . . . former teachers.”] Document 104 of ECP-1. |
| 70 | [an illegitimate child . . . staid Switzerland;] ECP-1; Renn and Schulmann (1992); Einstein and Marić (1992). |
| 70 | [Most of these he spent studying and thinking] I am speculating, based on various biographies of Einstein, that he spent most of his free hours in this way. |
| 70 | [“He was sitting in his study . . . went on working.”] Seelig (1956), as quoted by Clark (1971). |
| 70 – 71 | [Sometimes it helped . . . “I could not have found . . . whole of Europe.”] But see the discussion, on page xxvi of Renn and Schulmann (1992), of the contributions that Besso made to Einstein’s work. |
| 77 | [This proof is essentially . . . devised by Einstein in 1905.] Section 2 of Document 23 of ECP-2. |
| 78 | [Indeed, a wide variety . . . in just this way.] See, e.g., the appendix in Will (1986). |
| 79 | [ Having deduced that space . . . to his principle of relativity: ] As Pais (1982, Section 6b.6) makes clear, Henri Poincaré formulated a primitive version of the principle of relativity (calling it the “relativity principle”) one year before Einstein, but was unaware of its power. |
| 83 | [Einstein’s article . . . was published.] Document 23 of ECP-2. |
C HAPTER 2
| 87 | General comments about Chapter 2: Most of this chapter’s material about Einstein’s life comes from the standard biographies of him: Pais (1982), Hoffman (1972), Clark (1971), Einstein (1949), and Frank (1947). For most of the historical perspective and quotations in Chapter 2, which I have gleaned from these standard biographies, I do not give individual citations below. Much new historical material will become available in the next few years, with the gradual publication of Einstein’s collected papers: the volumes that follow the already published ECP-1 and ECP-2. |
|
The intellectual route that Einstein followed to get from special relativity to general relativity was basically that described in this chapter. However, of necessity I have simplified his route substantially; and for clarity, I have described the route in modern language rather than in the language that Einstein used. For a careful historical reconstruction of Einstein’s intellectual route, see Pais (1982). |
|
| 87 | [The views of space and time . . . independent reality.] Hermann Minkowski’s address was delivered at the 80th Assembly of German Natural Scientists and Physicians, at Cologne, 21 September 1908. An English translation has been published in Lorentz, Einstein, Minkowski, and Weyl (1923). |
| 94 | [The other, a peculiarity in the Moon’s . . . misinterpretation of the astronomers’ measurements.] The Moon appeared to be speeding up ever so slightly in its motion around the Earth, an effect that Newton’s gravitational law could not explain. In 1920 G. I. Taylor and H. Jeffreys realized that, in fact, the Moon was not speeding up. Rather, the Earth’s spin was slowing down due to the gravitational pull of the Moon on high-tide water in the Earth’s oceans. By comparing the Moon’s steady motion to the Earth’s slowing spin, astronomers had incorrectly inferred a lunar speedup. See Smart (1953). |
| 96 | [review article . . . Radioaktivität und Elektronik ] An English translation of Einstein’s beautiful review article is published as Document 47 of ECP-2. |
| 100 | [Einstein discovered gravitational time dilation . . . presented in Box 2.4,] Einstein’s argument as presented in Box 2.4 was originally published in Einstein (1911). |
| 100 | [When starting to write his 1907 review article, . . . Radioaktivität und Elektronik ] Document 47 of ECP-2. |
| 103 | [Einstein’s life as a professor . . . he was brilliant.] See Frank (1947), pages 89–91. |
| 117 | [These conclusions . . . on 25 November.] Einstein (1915). |
| 118 – 119 | Box 2.6: Remark for readers who are familiar with the mathematical formulation of general relativity: The description of the Einstein field equation given in this box corresponds to the mathematical relation R tt = 4π G(T tt + T xx + T yy + T zz ), where R tt is the time–time component of the Ricci curvature tensor, G is Newton’s gravitation constant, T tt is the density of mass expressed in energy units (see Box 5.2), and T xx + T yy + T zz is the sum of the principal pressures along three orthogonal directions. See page 406 of MTW. This “time–time” component of the Einstein field equation, when imposed in all reference frames, guarantees that the other nine components of the field equation are satisfied. |
| 119 | [As I browse . . . (a browsing which, . . . into English!)J Einstein’s personal papers and the rights to some of his published papers were tied up in a legal battle for several decades. The Russian edition of his collected works was produced and published at a time when the Soviet Union did not adhere to the International Copyright Convention. The far more complete English edition is now being published, very gradually; the first two volumes are ECP-1 and ECP-2. |
C HAPTER 3
| 121 | [“The essential result of this investigation . . . reality.”] Einstein (1939). |
| 122 | [In 1783 John Michell . . . should look like.] Michell (1784). For discussions of this work see Gibbons (1979), Schaffer (1979), Israel (1987), and Eisenstaedt (1991). |
| 123 | [Thirteen years later, . . . subsequent editions of his book.] Laplace (1796, 1799). For discussions of Laplace’s publications on dark stars, see Israel (1987) and Eisenstaedt (1991). Eisenstaedt discusses the attempts and failure to verify, observationally, Michell’s prediction that light emitted by massive stars is affected by their gravitational pull, and the contribution that this failure might have had to Laplace’s deletion of dark stars from the third edition of his book. |
| 124 | [Schwarzschild mailed to Einstein . . . curvature inside the star.] Schwarzschild(1916a,b). |
| 131 | [Jim Brault . . . Einstein’s prediction.] Brault (1962). For a detailed discussion of tests of Einstein’s general relativistic laws of gravity see Will (1986). |
| 131 – 132 | [However, few were . . . highly compact stars.] For a detailed discussion of the early history of people’s reaction to the Schwarzschild geometry and research on it, see Eisenstaedt (1982). A broader-brushed history that covers the period from 1916 to 1974 will be found in Israel (1987). |
| 135 | [In 1939, Einstein published . . . cannot exist.] Einstein (1939). |
| 136 | [As backing for . . . Einstein believed.] Schwarzschild (1916b). |
| 138 | [“I am sure . . . to that faith.”] Israel (1990). |
| 139 | [“There is a curious . . . dream of.”] Israel (1990). |
C HAPTER 4
| 140 | General comment about Chapter 4: The historical aspects of this chapter are based largely on (i) personal conversations with S. Chandrasekhar over the past twenty-five years, (ii) a taped interview with him (INT-Chandrasekhar), (iii) a book about Eddington by him (Chandrasekhar, 1983a), and (iv) a beautiful biography of him (Wali, 1991). I do not cite specific sources for specific items, except in special cases. Chandrasekhar’s scientific publications on white dwarfs are collected together in Chandrasekhar (1989). |
| 141 – 142 | [Especially interesting was . . . Royal Astronomical Society .] Fowler (1926). |
| 142 | [Fowler’s article pointed . . . Arthur S. Eddington,] Eddington (1926). |
| 143 | Footnote 2: For a detailed discussion of the difficulties Adams faced and the errors that he made in his measurements, see Greenstein, Oke, and Shipman (1985). This reference also gives information about observational studies of Sirius B up to 1985. |
| 150 | [Chandrasekhar worked out . . . in pressure.] Here I have taken literary license in two ways. First, Fowler (1926) had already computed the resistance to compression, so Chandrasekhar was merely checking Fowler’s calculation. Second, this is not the route by which Chandrasekhar carried out his computation (INT-Chandrasekhar), though it is mathematically equivalent to the true route. This route is the one that is easiest for me to explain; the true route entailed computing the electrons’ pressure as an integral over their momentum space. |
| 152 | [Finally, a full year . . . published.] Chandrasekhar (1931). |
| 152 | Footnote 4: Stoner (1930). This contribution by Stoner is briefly mentioned by Chandrasekhar (1931). For a discussion of the work of Stoner and related work by Wilhelm Anderson, see Israel (1987). |
| 153 | [In late 1934 . . . in Estonia.] Anderson (1929), Stoner (1930). |
| 154 | Figure 4.3: The masses and circumferences of white dwarfs as shown in this figure, and Chandrasekhar’s results for the interior structures of white- dwarf stars, were later published in Chandrasekhar (1935). |
| 160 | [“The star has to go on radiating . . . in this absurd way!”] Eddington (1935a). For further details of Eddington’s specious arguments see Eddington (1935b). |
| 161 – 162 | [To Leon Rosenfeld . .. “If Eddington is right,. . . Eddington’s statements”] Wali (1991). |
| 162 | [in Paris in 1939, . . . “Out there we don’t believe in Eddington.”] Wali (1991). |
| 162 | [If nature provided no law . . . white-dwarf grave.] I was told this in an authoritative fashion by an eminent Caltech astronomy professor when I was an undergraduate in 1958–62. It is my strong personal impression from that era that most astronomers were taking this view and had done so since the early 1940s, but I cannot be sure. |
| 163 | [“I felt that. . . into something else.”] Quoted by Wali (1991). |
| 163 | [To Eddington, the treatment . . . astronomical establishment.] This interpretation of Eddington’s behavior was suggested to me by Werner Israel, in a critique of an early version of this chapter; I believe it accords well with the historical record. |
C HAPTER 5
| 164 | General comment about Chapter 5: The historical aspects of this chapter ate based in large part (i) on my interviews with participants in the events described, or with their scientist colleagues and friends (INT-Baym, INT- Braginsky, INT-Eggen, INT-Fowler, INT-Ginzburg, INT-Greenstein, INT-Harrison, INT-Khalatnikov, INT-Lifshitz, INT-Sandage, INT-Serber, INT-Volkoff, INT-Wheeler), and (ii) on my reading of the scientific papers the participants wrote. For general background on the history of physics in the 1920s and 1930s, I have relied somewhat on Kevles (1971), and for background on the history of Soviet physics, on Medvedev (1978). Useful information and background about Landau came from Livanova (1980) and Gamow (1970), about Oppenheimer from Rabi et al. (1969) and Smith and Weiner (1980), and about the development of Wheeler’s ideas from his research notebooks, Wheeler (1988). In some places I have relied on other sources cited below. |
| 164 | [“By the time I knew Fritz . . . wrong,”] INT-Fowler. |
| 164 | [Jesse Greenstein . . . “a self-proclaimed genius . . . other people.”] INT-Greenstein, and Greenstein (1982). |
| 165 | [He even went on the air . . . popularize his neutron stars.] Zwicky (1935). |
| 166 | [“Zwicky called Baade . . . same room,” recalls Jesse Greenstein.] INT- Greenstein. |
| 168 | [(Today we know, . . . factor of 10,] Baade (1952). |
| 168 | [By combining Baade’s knowledge . . . larger factor, 10 million,] These are Baade and Zwicky’s numbers, as they appear in the abstract of a talk that is replicated in Figure 5.2 (Baade and Zwicky, 1934a), except for the “10,000 and perhaps 10 million,” which come from their more detailed paper on the issue (Baade and Zwicky, 1934b). Their error resulted from assuming that when the supernova is brightest, the circumference of its hot, radiating gas is in the range of 1 to 100 solar circumferences. In fact, the circumference is far larger than this, and when one traces through their argument, this results in far less ultraviolet light and X-rays. |
| 171 | [The neutron arrived . . . it seemed to Zwicky.] In this section and throughout Chapter 5, I attribute to Zwicky the concept of a neutron star and its consequences for supernovae and cosmic rays, although the publication of the ideas was joint with Baade. Giving Zwicky the credit for the ideas (and Baade the credit for the key understanding of the observational data) is an informed speculation based on my discussions with their scientist colleagues: INT-Eggen, INT-Fowler, INT-Greenstein, INT-Sandage. |
| 174 | Figure 5.2: Baade and Zwicky (1934a). For some justification of the numbers in the abstract see the more detailed presentation in Baade and Zwicky (1934b). |
| 178 | [Landau’s publication . . . cry for help:] This interpretation of Landau’s publication was explained to me by his closest, lifelong friend, Evgeny Michailovich Lifshitz (INT-Lifshitz). |
| 180 | [A fellow postdoctoral. . . “I vividly remember . . . of the paper.”] Quoted in Livanova (1980). |
| 180 – 181 | [“All the nice girls . . . are left,”] Quoted in Livanova (1980). |
| 181 | [As George Gamow, . . . “Russian science . . . capitalistic countries.”] Gamow (1970). |
| 181 | [In 1936 Stalin, . . . were destroyed.] The statistics on imprisonments and deaths under Stalin are somewhat uncertain. Medvedev (1978) gives what are perhaps the most reliable numbers available in the 1970s. However, in the late 1980s glasnost made possible the public dissemination of information that drove the numbers upward. The numbers I quote are an overall assessment made by Russian friends of mine who have studied the issue in some depth in the light of the glasnost revelations. |
| 182 | [Arthur Eddington . . . nuclear fusion; ] Chapter 11 of Eddington (1926) and references therein. |
| 184 | [Landau had actually . . . fail in atomic nuclei.] Landau (1932). |
| 184 | [In late 1937, Landau wrote a manuscript] Landau’s manuscript was published in Landau (1938). Unbeknownst to Landau, his close friend George Gamow had already published the same idea (Gamow, 1937). Gamow had escaped from the U.S.S.R. in 1933, shortly after Stalin’s iron curtain descended (see Gamow, 1970), but before escaping he had learned Landau’s original pre-neutron idea of keeping a star hot by a dense central core. After the neutron was discovered, it was natural that Gamow and Landau (now out of contact with each other) would independently reinterpret Landau’s 1931 core as a neutron core. |
| 185 – 186 | [Landau sent Bohr . . . “The new idea of L. Landau is excellent and very promising.”] Landau’s closest personal friend, Evgeny Michailovich Lifshitz, called my attention to this correspondence in 1982 (INT-Lifshitz) and explained to me the history behind it, as recounted here. After Lifshitz’s death, the full correspondence—including that between Kapitsa and Molotov, Kapitsa and Stalin, and Kapitsa and Beria, which ultimately produced Landau’s release from prison—was published in Khalatnikov (1988). The excerpts quoted here are my own translation from the Russian. |
| 186 | [—though in Landau’s case, . . . KGB files:] Gorelik (1991). |
| 186 – 187 | [Landau was lucky . . . (Superfluidity had been discovered . . . power of Soviet science.)] See note to pages 185–186. |
| 188 | [“Well, Robert, . . . damned word.”] Quoted in Royal (1969). |
| 188 – 189 | [“Oppie . . . twenty-five dollars a month.”] Serber (1969). |
| 191 | [(As of the early 1990s, . . . Landau’s mechanism.)] These giant stars are thought to be created in binary star systems when one star implodes to become a neutron star, and then, much later, spirals into the core of its companion star and takes up residence there. ‘These peculiar beasts have come to be called “Thorne–Żytkow objects” because Anna Żytkow and I were the first to compute their structures in detail. See Thorne and Żytkow (1977); also Cannon et al. (1992). |
| 191 | [they submitted their critique . . . “An estimate of Landau . . . of the Sun.”] Oppenheimer and Serber (1938). |
| 192 | [In the 1990s,. . . 3 solar masses,] Shapiro and Teukolsky (1983), Hartle and Sabbadini (1977). |
| 193 – 196 | Box 5.4: In this box, most of my description of the sequence of steps by which the research was done is informed speculation, based on an interview with Volkoff (INT-Volkoff), the Tolman archives (Tolman, 1948), and the participants’ publications (Oppenheimer and Volkoff, 1939; Tolman, 1939). |
| 195 | [On 19 October, . . . more formulas.] The correspondence between Tolman and Oppenheimer is archived in Tolman (1948). |
| 195 – 196 | [“I remember being . . . my calculations.”] INT-Volkoff. |
| 196 | [There must still be . . . several solar masses.] This conclusion was published in Oppenheimer and Volkoff (1939). Tolman’s analytic analyses, on which Oppenheimer and Volkoff relied for their estimates of the effect of nuclear forces, were published in Tolman (1939). |
| 197 | [In March 1956, Wheeler . . . and Oppenheimer and Volkoff.] Volume 4, pages 33–40 of Wheeler (1988). |
| 199 | [Wheeler was superbly prepared . . . hydrogen bomb] For details of Wheeler’s background and earlier work see Wheeler (1979) and Thorne and Zurek (1986). |
| 200 – 202 | Box 5.5: This equation of state (the fruit of the work of Harrison and Wheeler) was published in Harrison, Wakano, and Wheeler (1958), and in greater detail in Harrison, Thorne, Wakano, and Wheeler (1965). The more recent, solid curve at and above nuclear densities (10 14 grams per cubic centimeter) is an approximation to various modern equations of state as reviewed by Shapiro and Teukolsky (1983). |
| 203 | Figure 5.5: From Harrison, Wakano, and Wheeler (1958) and Harrison, Thorne, Wakano, and Wheeler (1965). The solid neutron-star curve is an approximation to various modern computations as reviewed by Shapiro and Teukolsky (1983). |
| 206 | [Thus, his article with Volkoff . . . “On Massive Neutron Cores.”] Oppenheimer and Volkoff (1939). |
| 207 | [His best effort . . . “On the Theory and Observation of Highly Collapsed Stars.”] Zwicky (1939). |
| 208 | [Isidore I. Rabi, . . . “[I]t seems to me . . . had already gone.”] Rabi et al. (1969). |
C HAPTER 6
| 209 | General comment about Chapter 6: The historical aspects of this chapter are based in large part on the following: (i) my interviews with participants in the events described, or with their scientist colleagues and friends (INT-Braginsky, INT-Finkelstein, INT-Fowler, INT-Ginzburg, INT-Harrison, INT-Lifshitz, INT-Misner, INT-Serber, INT-Wheeler, INT-Zel’dovich), (ii) my own participation in a small portion of the history, (iii) my reading of the scientific papers the participants wrote, (iv) the descriptions of the American nuclear weapons projects in Bethe (1982), Rhodes (1986), Teller (1955), and York (1976), (v) the descriptions of the Soviet nuclear weapons projects and other events in the U.S.S.R. in Golovin (1973), Medvedev (1978), Ritus (1990), Romanov (1990), and Sakharov (1990), and (vi) John Wheeler’s research notebooks (Wheeler, 1988). |
| 209 – 211 | [It was Tuesday, 10 June 1958 . . . “It is very difficult to believe ‘gravitational cutoff is a satisfactory answer,”] A written version of Wheeler’s lecture and the interchange of comments between Wheeler and Oppenheimer are published in Solvay (1958). |
| 210 | [“there seems no escape . . . [below about 2 Suns]”] This quote is paraphrased from Harrison, Wakano, and Wheeler (1958), with minor changes of detail to fit the phraseology and conventions of this book. |
| 212 | [“Hartland pooh-poohed . . . liberal politics.”] INT-Serber. |
| 212 | [“Oppie was extremely cultured;. . . most independent.”] INT-Fowler. |
| 212 | [“Hartland had more talent. . . rest of us did.”] INT-Serber. |
| 212 | [Before embarking . . . quick survey of the problem.] Here I am speculating; I do not know for sure that he carried out such a quick survey, but based on my understanding of Oppenheimer and the contents of the paper he wrote when the research was finished (Oppenheimer and Snyder, 1939), I strongly suspect that he did. |
| 216 – 217 | [By scrutinizing those formulas, . . . looks on the star’s surface,] Oppenheimer and Snyder published the results of their research in Oppenheimer and Snyder (1939). |
| 219 | [At Caltech, for example, . . . was very convinced.] INT-Fowler. |
| 219 | [There Lev Landau, . . . human mind to comprehend.] INT-Lifshitz. |
| 220 | [“In personality they . . . I chose Breit.”] Wheeler (1979). This reference is an autobiographical account of Wheeler’s research in nuclear physics. |
| 220 , 222 | [Wheeler and Bohr at Princeton . . . The Bohr–Wheeler article . . . Physical Review ] Bohr and Wheeler (1939), Wheeler (1979). Bohr and Wheeler did not name plutonium-239 by name in their paper, but Louis A. Turner inferred directly from their Figure 4 that it was an ideal nucleus for sustaining chain reactions, and proposed in a famous classified memorandum that it be used as the fuel for the atomic bomb (Wheeler, 1985). |
| 223 | [Zel’dovich and a close friend, . . . for all the world to see.] INT-Zel’dovich, Zel’dovich and Khariton (1939). |
| 223 | [Wheeler was the lead scientist . . . Nagasaki bomb.] For some details of Wheeler’s key role, see pages 2–5 of Klauder (1972). |
| 223 | [“If atomic bombs . . . at Los Alamos and Hiroshima.”] From a speech by Oppenheimer at Los Alamos, New Mexico, on 16 October 1945; see page 172of Goodchild (1980). |
| 223 | [“In some sort of crude sense . . . cannot lose.”] Page 174 of Goodchild (1980). |
| 223 – 224 | [ “As I look back . . . August 6, 1943.”] Wheeler (1979). |
| 225 | [While this massive effort. . . over to the American design.] These details were revealed by Khariton in a lecture in Moscow, which was reported in the New York Times of Thursday, 14 January 1993, page A5. |
| 225 | [accumulation of waste . . . square miles of countryside.] Medvedev (1979). |
| 226 – 227 | [“We base our recommendations . . . genocide.”] Report of 30 October 1949 from the General Advisory Committee to the U.S. Atomic Energy Commission. Reproduced in the appendix of York (1976). |
| 227 | [“Nine out of ten . . . stroke of genius.”] Bethe (1982). |
| 227 | [As Wheeler recalls, “We did an immense amount . . . get things out.”] INT-Wheeler. |
| 228 | [Wheeler recalls, “While I was starting . . . on the project.”] INT-Wheeler. |
| 229 | [“The program we had in 1949 . . . once you had it.”] USAEC (1984), p. 251. |
| 229 | [“I’m told . . . thermonuclear devices”] INT-Wheeler. |
| 229 | [In spring 1948, fifteen months before] There seems to be some confusion over the date on which the Soviet H-bomb design work was initiated. Sakharov (1990) dates it as spring 1948, but Ginzburg (1990) dates it as 1947. |
| 229 | [In June 1948, a second superbomb team] This is the date given by Sakharov (1990); Ginzburg (1990) places the date in 1947. |
| 229 | Footnote 3: Sakharov’s speculation is outlined in Sakharov (1990). Zel’dovich’s assertion was made verbally to close Russian friends, who transmitted it to me. |
| 230 | [“Our job is to lick Zel’dovich’s anus.”] Quoted to me by Vitaly Ginzburg, who was present. Sakharov was also present; in the English version of his memoirs (Sakharov, 1990), the quotation is expressed as “Our job is to kiss Zel’dovich’s ass.” For some of my own views on the complex relationship between Zel’dovich and Sakharov, see Thorne (1991). |
| 230 | [“that bitch, Zel’dovich.”] This quote by Landau has been passed on to me independently by several Soviet theoretical physicists. |
| 230 | [Sakharov proposed . . . lithium deuteride (LiD).] Romanov (1990). |
| 231 | [it was 800 times more powerful. . . Hiroshima.] The numbers I cite for the energy release in various bomb explosions are taken from York (1976). |
| 231 | [“I am under the influence . . . his humanity.”] Sakharov (1990). |
| 232 | [In March 1954, Sakharov . . . Teller–Ulam idea,] Romanov (1990), Sak harov (1990). Romanov, in an article in honor of Sakharov, attributes the discovery jointly to Sakharov and Zel’dovich. Sakharov says that “[s]everal of us in the theoretical departments came up with [this idea] at about the same time,” and he then leaves the impression that he himself deserves the greater share of the credit but says that “Zel’dovich, Yuri Trutnev, and others undoubtedly made significant contributions.”EBM pepst |
| 235 | [“In a great number of cases . . . not to grant clearance.”] USAEC (1954). |
| 235 | [Teller had “had the courage . . . deserved consideration,”] J. A. Wheeler, telephone conversation with K. S. Thorne, July 1991. |
| 235 | [Andrei Sakharov, . . . came to agree.] Sakharov (1990). |
| 239 | [At Livermore . . . produced a black hole.] The motivation for this research, a quest to understand supernovae and their roles as sources of cosmic rays, is described in Colgate and Johnson (1960). Colgate and White (1963, 1966) carried out the small-mass, supernova-forming simulations, using Newton’s description of gravity rather than Einstein’s. May and White (1965, 1966) did the large-mass, black-hole–forming simulations, using Einstein’s general relativistic description of gravity. |
| 240 – 241 | [To puzzle out the details . . . nearly identical to the Americans’.] Imshennik and Nadezhin (1964), Podurets (1964). |
| 244 | [“You cannot appreciate . . . true simultaneously,”] INT-Lifshitz. |
| 244 | [Then one day in 1958, . . . David Finkelstein,] Finkelstein (1958). |
| 244 | [Footnote 5: See, e.g., the discussions in Box 31.1 and Chapter 31 of MTW. |
| 245 | [Finkelstein discovered, quite by chance . . . and stellar implosion.] For Finkelstein’s description of how the discovery was made, see Finkelstein (1993). |
| 246 | [an article in Scientific American. ] Thorne (1967). |
| 254 | [In 1964 and 1965 . . . stellar implosion.] Harrison, Thorne, Wakano, and Wheeler (1965). |
| 256 | [He tried it out at a conference . . . “By reason . . . increase its gravitational attraction.”] Wheeler (1968). |
C HAPTER 7
| 258 | General comment about Chapter 7: The historical aspects of this chapter are based on (i) my own personal experience as a participant, (ii) my interviews with other participants (INT-Carter, INT-Chandrasekhar, INT-Detweiler, INT-Eardley, INT-Ellis, INT-Geroch, INT-Ginzburg, INT-Hartle, INT-Ipser, INT-Israel, INT-Misner, INT-Novikov, INT-Penrose, INT-Press, INT-Price, INT-Rees, INT-Sciama, INT-Smarr, INT-Teukolsky, INT-Wald, INT-Wheeler, INT-Zel’dovich), and (iii) my reading of the scientific papers the participants wrote. |
| 262 | [“There have been few occasions . . . consummated.”] Wheeler (1964b). |
| 266 | [hoop conjecture: ] I first published the concept of the hoop conjecture in a Festschrift volume in honor of Wheeler (Thorne, 1972), and in Box 32.3 of MTW. |
| 268 | [the idea that the implosion of a star . . . run backward.] This idea was called by Novikov and Zel’dovich the semiclosed universe. They ultimately published separate papers describing it: Zel’dovich (1962) and Novikov (1963). |
| 269 | [“Maybe you now don’t . . . but you will want to.”] INT-Novikov. |
| 269 | [“Yakov Boris’ch would . . . next day.”] INT-Novikov. |
| 274 | [To test this speculation . . . no magnetic field whatsoever.] The key ideas and initial calculations of this research were published in Ginzburg (1964); more complete mathematical details were worked out by Ginzburg and a young colleague, Leonid Moiseevich Ozernoy (Ginzburg and Ozernoy, 1964). |
| 275 | [Doroshkevich, Novikov, and Zel’dovich quickly . . . no protrusion] They published their analysis and conclusions in Doroshkevich, Zel’dovich, and Novikov (1965). (The order of the authors is alphabetic in the Russian language.) |
| 278 | [In London, Novikov presented . . . anything like it.] Readers can see the flavor of Novikov’s lecture in the influential review articles that he and Zel’dovich wrote shortly before the conference: Zel’dovich and Novikov (1964, 1965). |
| 278 | [The written version . . . in Russian.] Doroshkevich, Zel’dovich, and Novikov (1965); see note to page 275. |
| 279 | [The first was Werner Israel, . . . will become clear below] Israel’s analysis was published in Israel (1967). |
| 281 | [He got there third, after Novikov and after Israel,] Novikov (1969), de la Cruz, Chase, and Israel (1970), Price (1972). |
| 283 – 284 | [(The mechanism, . . . Ted Chase.)] de la Cruz, Chase, and Israel (1970). |
| 284 | [The field now threads the horizon, . . . leaving the hole unmagnetized] For a more detailed and complete discussion of the interaction of magnetic fields with a black hole, see Figures 10, 11, and 36 of Thorne, Price, and Macdonald (1986). |
| 285 | [The lion’s share . . . Mazur.] For a review and references, see Section 6.7 of Carter (1979); the subsequent, final stage was published in Mazur (1982) and Bunting (1983). |
| 288 | [John Graves and Dieter Brill, . . . charged black hole.] Graves and Brill (1960) and references therein. |
| 289 | [Roy Kerr had . . . outside a spinning star.] Kerr (1963). |
| 290 | [Within a year Carter . . . Richard Lindquist,] Carter (1966), Boyer and Lindquist (1967). |
| 290 | [Carter and others . . . possibly exist.] Carter (1979) and earlier references therein. |
| 290 | [Carter, by plumbing that mathematics, . . . should be.] Carter (1968). |
| 293 | [Werner Israel showed . . . always fail.] Israel (1986). |
| 294 | [In 1969, Roger Penrose . . . marvelous discovery.] Penrose (1969). |
| 295 | [Ted Newman . . . Robert Torrence.] Newman et al. (1965). |
| 295 | [In autumn 1971, Bill Press, . . . black hole itself.] Press (1971). |
| 297 | [The winner was Saul Teukolsky,] Teukolsky (1972). |
| 298 | [‘Teukolsky recalls vividly . . . “Sometimes when you play with mathematics, . . . terms together.”] INT-Teukolsky. |
| 298 | [Teukolsky himself, . . . its pulsations are stable.] Press and Teukolsky (1973). |
| 299 | [ The Mathematical Theory of Black Holes ] Chandrasekhar (1983b). |
C HAPTER 8
| 300 | [General comment about Chapter 8: The historical aspects of this chapter are based on (i) my own personal experience as a participant, (ii) my interviews with other participants (INT-Giacconi, INT-Novikov, INT-Rees, INT-Van Allen, INT-Zel’dovich), (iii) my reading of the scientific papers the participants wrote, and (iv) the following published accounts of the history: Friedman (1972), Giacconi and Gursky (1974), Hirsh (1979), and Uhuru (1981). |
| 301 | [“Such an object. . . another star”] Wheeler (1964a). |
| 301 | [If you are Zel’dovich . . . stellar implosion.] Twenty-two years later, in 1986, Zel’dovich expressed to me regret that he had not been more open-minded about the issue of what goes on inside black holes; INT-Zel’dovich. |
| 306 | [Together, Guseinov and Zel’dovich . . . the catalogs.] Zel’dovich and Guseinov (1965). |
| 307 | [By searching through . . . eight black-hole candidates.] Trimble and Thorne (1969). |
| 307 | [Fortunately, his brainstorming . . . New York.] Salpeter (1964), Zel’dovich (1964). |
| 308 | [Zel’dovich and Novikov together . . . infalling gas idea] Novikov and Zel’dovich (1966). |
| 309 | [“the rocket returned . . . on impact.”] Friedman (1972). |
| 311 | [they announced their discovery: . . . had predicted ] Giacconi, Gursky, Paolini, and Rossi (1962). |
| 318 | [(suggested in 1972 by Rashid Sunyaev, . . . Zel’dovich’s team)] Sunyaev (1972). |
C HAPTER 9
| 322 | General comment about Chapter 9: The historical aspects of this chapter are based on (i) my own personal experience as a peripheral participant from 1962 onward, (ii) my interviews with several participants (INT-Ginzburg, INT-Greenstein, INT-Rees, INT-Zel’dovich), (iii) my reading of the scientific papers the participants wrote, and (iv) the following published and unpublished accounts of the history: Hey (1973), Greenstein (1982), Kellermann and Sheets (1983), Struve and Zebergs (1962), and Sullivan (1982, 1984). |
| 323 | [Cosmic radio waves . . . 1932 by Karl Jansky,] Jansky (1932). |
| 323 – 324 | [The two exceptions . . . Jansky was seeing.] Whipple and Greenstein (1937). |
| 324 | [“I never met . . . not one astronomer,”] INT-Greenstein. |
| 324 | [So uninterested . . . call number W9GFZ.] For Reber’s own historical description of his work, see Reber (1958). |
| 327 | [In 1940, having made . . . paper for publication.] Reber (1940). |
| 327 | [Greenstein describes Reber as “the ideal American inventor . . . a million dollars.”] INT-Greenstein. |
| 327 | [“The University didn’t want . . . independent cuss,”] INT-Greenstein. |
| 330 | [The first crucial benchmark, . . . radio sources must lie.] Bolton, Stanley, and Slee (1949). |
| 331 | [When Baade developed . . . two galaxies colliding with each other] Baade and Minkowski (1954). |
| 333 | [R. C. Jennison and M. K. Das Gupta . . . opposite sides of the “colliding galaxies.”] Jennison and Das Gupta (1953). |
| 334 | [Greenstein organized . . . 5 and 6 January 1954.] The proceedings of this conference are published in Washington (1954). |
| 335 | [The mental block . . . Maarten Schmidt,] Schmidt (1963). |
| 336 | [Greenstein turned,. . . 37 percent of the speed of light.] Greenstein (1963). |
| 337 | [Harlan Smith . . . as short as a month.] Smith (1965). |
| 339 | [Building on seminal ideas . . . fill interstellar space] Alfvén and Herlofson (1950), Kiepenheuer (1950), Ginzburg (1951). For a discussion of the history of this work see Ginzburg (1984). |
| 339 | [Geoffrey Burbidge . . . 100 percent efficiency.] Burbidge (1959). |
| 341 | [To foster dialogue . . . Dallas, Texas.] The proceedings of this conference are published in Robinson, Schild, and Shucking (1965). |
| 342 | [So, as Kerr got up to speak,. . . picked up pace.] This description is from my own vivid memory of the conference. |
| 343 | [In 1971, this suggested . . . that powers quasars.] Rees (1971). |
| 343 | [Malcolm Longair,. . . electromagnetic waves.] Longair, Ryle, and Scheuer (1973). |
| 346 | [The idea that gigantic black holes . . . Edwin Salpeter and Yakov Borisovich Zel’dovich] Salpeter (1964), Zel’dovich (1964). |
| 346 | [A more complete . . . by Donald Lynden-Bell,] Lynden-Bell (1969). |
| 346 | [How can a black hole . . . answer in 1975:] Bardeen and Petterson (1975). |
| 347 – 348 | [How strong will the swirl of space be . . . nearly its maximum possible rate] Bardeen (1970). |
| 348 | [First, Blandford and Rees realized,] Blandford and Rees (1974). |
| 348 | [Second, . . . Lynden-Bell pointed out,] Lynden-Bell (1978). |
| 348 | [Third, Blandford realized,] Blandford (1976). |
| 350 | [The fourth method . . . Blandford–Znajek process .] Blandford and Znajek (1977). |
| 351 | [If quasars and radio galaxies are powered by the same kind of black-hole engine,] For more detailed discussions of the present state of our understanding of quasars, radio galaxies, jets, and the roles of black holes and their accretion disks as the central engines that power them, see, e.g., Begelman, Blandford, and Rees (1984) and Blandford (1987). |
| 354 | [The evidence for such a hole . . . far from firm.] See, e.g., Phinney (1989). |
C HAPTER 10
| 357 | General comment about Chapter 10: The historical aspects of this chapter are based on (i) my own personal experience as a participant, (ii) my interviews with several participants (INT-Braginsky, INT-Drever, INT-Forward, INT-Grishchuk, INT-Weber, INT-Weiss), and (iii) my reading of scientific papers the participants wrote. For more technical overviews of gravitational radiation and efforts to detect it, see, e.g., Blair (1991) and Thorne (1987). |
| 366 | [While Weber was publishing his concept,] Weber (1953). |
| 366 – 367 | [Through late 1957, . . . broadside to the incoming waves] The fruits of Weber’s work were published in Weber (1960, 1961). |
| 367 | [His sole guide . . . near the critical circumference.] Letter from Weber to me, dated 1 October 1992; Weber did not publish this argument at the time. Weber’s colleague Freeman Dyson was the first to show that nature is likely to produce gravitational-wave bursts near the frequencies Weber had chosen (Dyson, 1963). |
| 369 | [However, in the early 1970s, . . . a reality.] Weber’s announcement of observational evidence for gravitational waves was made in Weber (1969). The ensuing experimental activity and controversy over whether waves had really been detected are documented, e.g., in deSabbata and Weber (1977) and papers cited therein. For a sociological study of the controversy see Collins (1975, 1981). |
| 369 | [two-month summer school] The lectures presented at the summer school, including Weber’s, were published in DeWitt and DeWitt (1964). |
| 372 | [During our 1969 meeting, . . . ultimate limitation.] This initial version of Braginsky’s warning was published in Braginsky (1967). |
| 372 | [However, in 1976,. . . uncertainty principle .] The clarified warnings were published in Braginsky (1977) and Giffard (1976), and the uncertainty principle origin of the limit was explained in Thorne, Drever, Caves, Zimmermann, and Sandberg (1978). |
| 375 | [Roughly 10 -21 was the answer,] See, e.g., the quasi-transcript of a 1978 conference discussion in Epstein and Clark (1979). |
| 375 | [We both found the answer . . . different routes.] Braginsky, Vorontsov, and Khalili (1978); Thorne, Drever, Caves, Zimmermann, and Sandberg (1978). |
| 378 | [In principle it would be possible to widen the bars’ bandwidths] Michelson and Taber (1984). |
| 383 | [Interferometers for gravitational-wave detection . . . as did Robert Forward and colleagues] Gertsenshtein and Pustovoit (1962), Weber (1964), Weiss (1972), Moss, Miller, and Forward (1971). |
| 383 | [and Drever had added . . . to their design.] See, e.g., Drever (1991) and references therein. |
| 387 | [he redirected most of his own team’s efforts . . . and modest funds.] See Braginsky and Khalili (1992). |
| 391 | [A key to success in our endeavor . . . or LIGO .] For an overview of the plans for LIGO see Abramovici et al. (1992). |
C HAPTER 11
| 397 | General comment about Chapter 11: The (rather minor) historical aspects of this chapter are based on (i) my own personal experience as a participant, (ii) my interviews with two other participants (INT-Damour, INT-Wald), (iii) my reading of scientific papers the participants wrote, and (iv) my experience as a student in a course on paradigms and scientific revolutions taught by Thomas Kuhn at Princeton University in 1965. |
| 401 | [ The Structure of Scientific Revolutions ] Kuhn (1962). |
| 403 | [This freedom carries power.] Richard Feynman, one of the greatest physicists of our century, described beautifully the power of having several different paradigms at one’s fingertips in his lovely little book The Character of Physical Law (Feynman, 1965). Note, however, that he never uses the word “paradigm,” and I suspect that he never read Thomas Kuhn’s writings. Kuhn described how people like Feynman operate; Feynman just operated that way. |
| 403 | [That is why physicists . . . supplement to it.] The flat spacetime paradigm was devised more or less independently by a number of different people; it is known, technically, as a “field theory in flat spacetime formulation of general relativity.” For an overview of its history and concepts, see the following passages in MTW: Sections 7.1 and 18.1; Boxes 7.1, 17.2, and 18.1; Exercise 7.3. For an elegant generalization of it, which elucidates its relationship to the curved spacetime paradigm, see Grishchuk, Petrov, and Popova (1984). |
| 406 | [In 1971 Hanni and Ruffini, . . . Jeff Cohen] Cohen and Wald (1971), Hanni and Ruffini (1973). |
| 407 | [Five years later Roger Blandford . . . power jets] Blandford and Znajek (1977). |
| 409 | [During 1977 and 1978, Znajek and . . . pictorial interpretation:] Znajek (1978), Damour (1978). |
| 409 | [ Black Holes: The Membrane Paradigm .] Thorne, Price, and Macdonald (1986). See also Price and Thorne (1988). |
C HAPTER 12
| 412 | General comment about Chapter 12: The historical aspects of this chapter are based on (i) my own personal experience as a participant, (ii) my interviews with other participants (INT-DeWitt, INT-Eardley, INT-Hartle, INT-Hawking, INT-Israel, INT-Penrose, INT-Unruh, INT-Wald, INT-Wheeler, INT-Zel’dovich), (iii) my reading of scientific papers the participants wrote, and (iv) the following published accounts of the history: Bekenstein (1980), Hawking (1988), Israel (1987). |
| 412 | [The Idea hit . . . so quickly.] This and the subsequent description of how Hawking arrived at the idea come from INT-Hawking and Hawking (1988). Hawking published the details and consequences of his idea, as sketched in the first section of this chapter, “Black Holes Grow,” in Hawking (1971b, 1972, 1973). |
| 414 | [following Roger Penrose’s lead,] Penrose (1965). |
| 414 | Box 12.1: Hawking (1972, 1973). |
| 417 | [Stephen Hawking was not the first . . . Werner Israel] INT-Israel, INT-Penrose, INT-Hawking. |
| 417 | [Penrose’s amazing 1964 discovery . . . singularity at its center.] Penrose (1965). |
| 418 | Box 12.2: Hawking (1972, 1973). |
| 419 | [Hawking and James Hartle . . . gravity of other bodies.] Hawking and Rartle (1972). |
| 422 | [Demetrios Christodoulou . . . equations of thermodynamics.] Christodoulou (1970). |
| 425 | [Jacob Bekenstein was not persuaded.] Bekenstein describes this and the controversy with Hawking that followed in Bekenstein (1980). Bekenstein published his black-hole entropy conjecture and his arguments for it in Bekenstein (1972, 1973). |
| 426 | [Les Houches summer school,] The proceedings of the 1972 summer school were published in DeWitt and DeWitt (1973). |
| 427 | [Bardeen, Carter, and Hawking . . . laws of black-hole mechanics ] Bardeen, Carter, and Hawking (1973). |
| 428 | [Zel’dovich had brought me to Moscow . . .] Charles Misner and John Wheeler accompanied me on my June 1971 visit to Moscow, but they were not with me at Zel’dovich’s apartment during the discussion described in the following paragraphs. |
| 429 | [Zel’dovich, his eyes dancing, . . .] I have reconstructed the following conversation from memory, and have translated it into less technical language than we actually used. |
| 433 | [Zel’dovich, however, did not forget; . . . his paper was published] Zel’dovich (1971). |
| 434 – 435 | [Starobinsky described Zel’dovich’s conjecture . . . does, indeed, radiate.] Zel’dovich and Starobinsky (1971). |
| 435 | [Then came a bombshell.] Hawking describes, in Hawking (1988), how he arrived at his “bombshell” discovery that all black holes radiate. He published the discovery and its implications in Hawking (1974, 1975, 1976). |
| 437 | [This and the demand for a perfect mesh,. . . almost completely.] See, e.g., Wald (1977). |
| 437 | Footnote 11: Wald (1977). |
| 439 | [Perhaps the simplest. . . particles rather than waves:] Hawking (1988). |
| 442 | [Gradually . . . new understanding embodied in Figure 12.3.] Chapter 8 of Thorne, Price, and Macdonald (1986), and references therein. |
| 444 | Box 12.5: Davies (1975), Unruh (1976), Unruh and Wald (1982, 1984). |
| 446 | [a highly abstract proof . . . in 1977.] Gibbons and Hawking (1977). |
| 446 | [The total lifetime, . . . Don Page] Page (1976). |
| 447 | [Detailed calculations by Hawking, . . . to produce tiny holes.] E.g., Hawking (1971a); Novikov, Polnarev, Starobinsky, and Zel’dovich (1979). |
| 447 | [The absence of excess gamma rays . . . soft equation of state.] Page and Hawking (1975); Novikov, Polnarev, Starobinsky, and Zel’dovich (1979). |
C HAPTER 13
| 449 | General comment about Chapter 13: The historical aspects of this chapter are based on (i) my own personal experience (though as an observer rather than a participant), (ii) my interviews with participants (INT-Belinsky, INT-DeWitt, INT-Geroch, INT-Khalatnikov, INT-Lifshitz, INT-MacCallum, INT-Misner, INT-Penrose, INT-Sciama, INT-Wheeler), and (iii) my reading of scientific papers the participants wrote. |
| 499 | [John Archibald Wheeler taught . . . outside the horizon.] Harrison, Wakano, and Wheeler (1958); Wheeler (1960). |
| 450 | [Wheeler retained his conviction . . . pursuing.] Wheeler (1964a,b); Harrison, Thorne, Wakano, and Wheeler (1965). |
| 450 | [J. Robert Oppenheimer and Hartland Snyder,] Oppenheimer and Snyder (1939). |
| 450 | [Perhaps Oppenheimer’s unwillingness to speculate,] See the last several pages of Chapter 5. |
| 451 | [The singularity predicted by the Oppenheimer–Snyder calculations] The singularity as described here is that in the vacuum outside the imploding star, and since the vacuum region is described by the Schwarzschild solution of Einstein’s equations, this singularity is often referred to as the singularity of the Schwarischild geometry. It is analyzed quantitatively, e.g., in Chapter 32 of MTW. |
| 451 | Figure 13.1: Ibid. |
| 453 | [One group, . . . general relativity fails] Wheeler (1960, 1964a,b); Harrison, Thorne, Wakano, and Wheeler (1965). |
| 453 | [A second group, . . . Khalatnikov and Evgeny Michailovich Lifshitz . . . could not be trusted.] This viewpoint and the calculations that led Khalatnikov and Lifshitz to it were published in Lifshitz and Khalatnikov (1960, 1963) and in Landau and Lifshitz (1962). |
| 454 | [Khalatnikov and Lifshitz . . . small perturbations .] Ibid. |
| 456 | [ The Classical Theory of Fields .] Landau and Lifshitz (1962). |
| 457 | Figure 13.4: It was obvious in the early 1960s to students in Wheeler’s group, where the Graves–Brill (1960) research had been done, that there must exist a solution to Einstein’s equations of the sort depicted here. However, I gather from a discussion with Penrose that researchers in most other groups did not become aware of it until the late 1960s. It was difficult to construct such solutions explicitly, and we in Wheeler’s group did not try, and did not publish anything on the issue. The first publication of the idea and the first attempt at an explicit solution, so far as I know, were by Novikov (1966). |
| 458 | [Hans Reissner and Gunnar Nordström . . . Dieter Brill and John Graves,] Graves and Brill (1960) and references therein. |
| 459 | [Roger Penrose grew up in a British . . .] This biographical discussion of Penrose comes largely from INT-Penrose and INT-Sciama. |
| 460 | [The seduction began in 1952,] Ibid. |
| 462 | [One day in late autumn of 1964, . . . ] INT-Penrose; Penrose (1989). |
| 462 | [“My conversation with Robinson . . . crossing the street.”] Penrose (1989). |
| 462 | [a short article for. . . Physical Review Letters ,] Penrose (1965). |
| 465 | [ global methods .] The global methods were codified in a classic book by Hawking and Ellis (1973). |
| 465 | [Hawking and Penrose in 1970 proved . . . big crunch.] Hawking and Penrose (1970). |
| 466 | [Lifshitz, though Jewish, . . . 1976.] From my private discussions with Lifshitz in the 1970s. |
| 466 | [Khalatnikov had two strikes against him;. . . come to London.] Letter from Khalatnikov to me, 18 June 1990. |
| 466 | [As he spoke in the packed London lecture hall, . . . Penrose, they asserted, was probably wrong.] From my own memory of the meeting and its aftermath. |
| 468 | [“Please, . . . submit it to Physical Review Letters ,”] Khalatnikov and Lifshitz (1970). See also Belinsky, Khalatnikov, and Lifshitz (1970, 1982). |
| 468 | [I carried the manuscript . . . published.] Ibid. |
| 470 | [Lev Davidovich Landau . . . great physics discoveries.] INT-Lifshitz, Livanova (1980). |
| 471 | [Curiously, topological techniques . . . Pimenov.] I learned this from Penrose. |
| 471 | [In 1950–59, Aleksandrov . . . that cannot.] Aleksandrov (1955, 1959). |
| 471 | [picked up and pushed further by Pimenov,] Pimenov (1968). |
| 473 | [(due to Khalatnikov and Lifshitz) . . . “unstable against small perturbations.”] Lifshitz and Khalatnikov (1960, 1963). |
| 473 | [The Reissner–Nordström . . . large universe] e.g., Novikov (1966). |
| 473 – 474 | [it is unstable . . . many different physicists.] In technical language, it is the inner Cauchy horizon of the Reissner–Nordström solution that is unstable. The conjecture is in Penrose (1968); the proofs are in Chandrasekhar and Hartle (1982) and earlier references cited therein. |
| 474 | [Belinsky, Khalatnikov, and Lifshitz . . . (This is the kind . . . holes.)] Belinsky, Khalatnikov, and Lifshitz (1970, 1982). |
| 474 | [Charles Misner . . . mixmaster oscillation ] Misner (1969). |
| 476 | [Just when does quantum gravity take over, . . . or less.] This was first deduced by Wheeler (1960), building on his own earlier ideas of vacuum fluctuations of the geometry of spacetime (Wheeler, 1955, 1957). |
| 476 | Footnote 2: The Planck–Wheeler time was introduced and its physical significance deduced by Wheeler (1955, 1957). |
| 476 – 477 | [Quantum gravity then radically changes . . . random, probabilistic froth,] This was first suggested by Wheeler (1960), and has been made more quantitative since via what is now called the “Wheeler–DeWitt equation.” See, e.g., the discussion in Hawking (1987). |
| 477 | [John Wheeler,. . . quantum foam ] Wheeler (1957, 1960). |
| 479 | [Clear answers . . . DeWitt.] See, e.g., Hawking (1987, 1988). |
| 479 | [The tidal forces . . . and gradually disappear.] Doroshkevich and Novikov (1978) showed that the singularity ages; Poisson and Israel (1990) and Ori (1991) deduced the details of the aging in idealized models; and Ori (1992) has tentatively shown that these models are good guides to the behavior of singularities in real black holes. |
| 481 | [Some implosions,. . . might actually create naked singularities.] For details of these simulations see Shapiro and Teukolsky (1991). |
| 482 | [Just four months . . . tiny naked singularity.] Hawking’s evidence was published in Hawking (1992a). |
C HAPTER 14
| 483 | General comment about Chapter 14: The historical aspects of this chapter are based almost entirely on my own experiences as a participant. |
| 485 – 486 | [Wormholes are not mere figments . . . in 1916,] Ludwig Flamm (1916) discovered that, with an appropriate choice of topology, the Schwarzschild (1916a) solution of Einstein’s equation describes an empty, spherical wormhole. |
| 487 | Figure 14.2: Kruskal (1960). |
| 490 | [We wrote slowly . . . American Journal of Physics, ] Morris and Thorne (1988). |
| 490 | [(the topic of the Hawking and Ellis book)] Hawking and Ellis (1973). |
| 491 | [ vacuum fluctuations near a hole’s horizon are exotic :] Hawking inferred this only very indirectly and somewhat tentatively from his discovery of black-hole evaporation. It was firmly demonstrated to be so six years later, by Candelas (1980). |
| 492 | [The answer has not come easily,. . . thereby makes them exotic.] See Wald and Yurtsever (1991) and other references cited therein. |
| 494 | [In 1955, John Wheeler,. . . quantum foam—] Wheeler (1955, 1957, 1960). |
| 497 | [In 1966, Robert Geroch . . . to travel backward in time,] Geroch (1967). Friedman, Papastamatiou, Parker, and Zhang (1988) have given an explicit example of wormhole creation of the sort envisioned by Geroch’s theorem. |
| 499 | Footnote 8: van Stockum (1937), Gödel (1949), Tipler (1976). |
| 508 | [Our paper was published,] Morris, Thorne, and Yurtsever (1988). |
| 509 | [we conjectured so in our paper.] Morris, Thorne, and Yurtsever (1988). |
| 509 | Footnote 12: Friedman and Morris (1991). |
| 511 | [Echeverria and Klinkhammer. . . two such trajectories.] Echeverria, Klinkhamnler, and Thorne (1991). |
| 513 – 514 | Box 14.2: Echeverria, Klinkhammer, and Thorne (1991). |
| 513 | [Robert Forward . . . discovered a third trajectory] Forward (1992). |
| 515 | [but there seem not to be . . . unresolvable paradox.] For a careful and fairly thorough technical discussion of the issue of paradoxes when one has a wormhole-based time machine, see Friedman et al. (1990). |
| 516 | [ California magazine, . . . on Palomar Mountain.] Hall (1989). |
| 517 | [Though we were helped . . . Konkowski] Hiscock and Konkowski (1982). |
| 520 | [a similar calculation by Valery Frolov . . . our results] Frolov (1991). |
| 521 | [we managed to change . . . got published] Kim and Thorne (1991). |
| 521 | [ the chronology protection conjecture ,] Hawking (1992b). |
| 521 | Footnote 14: Gott (1991). |
| 521 | [I am not willing to take . . . the laws of quantum gravity.] For a somewhat technical description of my 1993 reasons for skepticism about time machines, and a detailed overview of research on time machines up to spring 1993, see Thorne (1993) |
![]()
T APED I NTERVIEWS
Baym, Gordon. 5 September 1985, Champaign/Urbana, Illinois.
Belinsky, Vladimir. 27 March 1986, Moscow, U.S.S.R.
Braginsky, Vladimir Borisovich. 20 December 1982, Moscow, U.S.S.R.; 27 March 1986, Moscow, U.S.S.R.
Carter, Brandon. 6 July 1983, Padova, Italy.
Chandrasekhar, Subrahmanyan. 3 April 1982, Chicago, Illinois.
Damour, Thibault. 26 July 1986, Cargese, Corsica.
Detweiler, Steven. December 1980, Baltimore, Maryland.
DeWitt, Bryce. December 1980, Baltimore, Maryland.
Drever, Ronald W. P. 21 June 1982, Les Houches, France.
Eardley, Doug M. December 1980, Baltimore, Maryland.
Eggen, Olin. 13 September 1985, Pasadena, California.
Ellis, George. December 1980, Baltimore, Maryland.
Finkelstein, David. 8 July 1983, Padova, Italy.
Forward, Robert. 31 August 1982, Oxnard, California.
Fowler, William A. 6 August 1985, Pasadena, California.
Geroch, Robert. 2 April 1982, Chicago, Illinois.
Giacconi, Riccardo. 29 April 1983, Greenbelt, Maryland.
Ginzburg, Vitaly Lazarevich. December 1982, Moscow, U.S.S.R.; 3 February 1989,Pasadena, California.
Greenstein, Jesse L. 9 August 1985, Pasadena, California.
Grishchuk, Leonid P. 26 March 1986, Moscow, U.S.S.R.
Harrison, B. Kent. 5 September 1985, Provo, Utah.
Hartle, James B. December 1980, Baltimore, Maryland; 2 April 1982, Chicago, Illinois.
Hawking, Stephen W. July 1980, Cambridge, England (not taped).
Ipser, James R. December 1980, Baltimore, Maryland.
Israel, Werner. June 1982, Les Houches, France.
Khalatnikov, Isaac Markovich. 27 March 1986, Moscow, U.S.S.R.
Lifshitz, Evgeny Michailovich. December 1982, Moscow, U.S.S.R.
MacCallum, Malcolm. 30 August 1982, Santa Barbara, California.
Misner, Charles W. 10 May 1981, Pasadena, California.
Novikov, Igor Dmitrievich. December 1982, Moscow, U.S.S.R.; 28 March 1986, Moscow, U.S.S.R.
Penrose, Roger. 7 July 1983, Padova, Italy.
Press, William H. December 1980, Baltimore, Maryland.
Price, Richard. December 1980, Baltimore, Maryland.
Rees, Martin. December 1980, Baltimore, Maryland.
Sandage, Allan. 13 September 1985, Baltimore, Maryland.
Sciama, Dennis. 8 July 1983, Padova, Italy.
Serber, Robert. 5 August 1985, New York City.
Smarr, Larry. December 1980, Baltimore, Maryland.
Teukolsky, Saul A. 27 January 1985, Ithaca, New York.
Unruh, William. December 1980, Baltimore, Maryland.
Van Allen, James. 29 April 1973, Greenbelt, Maryland.
Volkoff, George. 11 September 1985, Vancouver, British Columbia.
Wald, Robert M. December 1980, Baltimore, Maryland; 2 April 1982, Chicago, Illinois.
Weber, Joseph. 20 July 1982, College Park, Maryland.
Weiss, Rainer. 7 July 1983, Padova, Italy.
Wheeler, John. December 1980, Baltimore, Maryland.
Zel’dovich, Yakov Borisovich. 17 December 1982, Moscow, U.S.S.R.; 22 and 27 March 1986, Moscow, U.S.S.R.
R EFERENCES
Abramovici, A., Althouse, W. E., Drever, R. W. P., Gürsel, Y., Kawamura, S., Raab, F. J., Shoemaker, D., Sievers, L., Spero, R. E., Thorne, K. S., Vogt, R. E., Weiss, R., Whitcomb, S. E., and Zucker, M. E. (1992). “LIGO: The Laser Interferometer Gravitational-Wave Observatory,” Science, 256, 325–333.
Aleksandrov, A. D. (1955). “The Space-Time of the Theory of Relativity,” Helvetica Physica Acta, Supplement, 4, 4.
Aleksandrov, A. D. (1959). “The Philosophical Implication and Significance of the Theory of Relativity,” Voprosy Filosofii No. 1, 67.
Alfvén, H., and Herlofson, N. (1950). “Cosmic Radiation and Radio Stars,” Physical Review, 78, 738.
Anderson, W. (1929). “Über die Grenzdichte der Materie und der Energie,” Zeitschrift für Physik 56, 851.
Baade, W. (1952). “Report of the Commission on Extragalactic Nebulae,” Transactions of the International Astronomical Union, 8, 397.
Baade, W., and Minkowski, R. (1954). “Identification of the Radio Sources in Cassiopeia, Cygnus A, and Puppis,” Astrophysical Journal , 119, 206.
Baade, W., and Zwicky, F. (1934a). “Supernovae and Cosmic Rays,” Physical Review, 45, 138.
Baade, W., and Zwicky, F. (1934b). “On Super-Novae,” Proceedings of the National Academy of Sciences, 20, 254.
Bardeen, J. M. (1970). “Kerr Metric Black Holes,” Nature, 226, 64.
Bardeen, J. M., Carter, B., and Hawking, S. W. (1973). “The Four Laws of Black Hole Mechanics,” Communications in Mathematical Physics, 31 , 161.
Bardeen, J. M., and Petterson, J. A. (1975). “The Lense–Thirring Effect and Accretion Disks around Kerr Black Holes,” Astrophysical Journal (Letters), 195, L65.
Begelman, M. C., Blandford, R. D., and Rees, M. J. (1984). “Theory of Extragalactic Radio Sources,” Reviews of Modern Physics, 56, 255.
Bekenstein, J. D. (1972). “Black Holes and the Second Law,” Lettere al Nuovo Cimento, 4 , 737.
Bekenstein, J. D. (1973). “Black Holes and Entropy,” Physical Review D, 7 , 2333.
Bekenstein, J. D. (1980). “Black Hole Thermodynamics,” Physics Today, January 24.
Belinsky, V. A., Khalatnikov, I. M., and Lifshitz, E. M. (1970). “Oscillatory Approach to a Singular Point in the Relativistic Cosmology,” Advances in Physics, 19, 525.
Belinsky, V. A., Khalatnikov, I. M., and Lifshitz, E. M. (1982). “Solution of the Einstein Equations with a Time Singularity,” Advances in Physics, 31 , 639.
Bethe, H. A. (1982). “Comments on the History of the H-Bomb;” Los Alamos Science, Fall 1982, 43.
Bethe, H. A. (1990). “Sakharov’s H-Bomb,” Bulletin of the Atomic Scientists, October 1990. Reprinted in Drell and Kapitsa (1991), p. 149.
Blair, D., ed. (1991). The Detection of Gravitational Waves (Cambridge University Press, Cambridge, England).
Blandford, R. D. (1976). “Accretion Disc Electrodynamics—A Model for Double Radio Sources,” Monthly Notices of the Royal Astronomical Society, 176, 465.
Blandford, R. D. (1987). “Astrophysical Black Holes,” in 300 Years of Gravitation, edited by S. W. Hawking and W. Israel (Cambridge University Press, Cambridge, England), p. 277.
Blandford, R. D., and Reexss, M. (1974). “A Twin-Exhaust Model for Double Radio Sources,” Monthly Notices of the Royal Astronomical Society, 169, 395.
Blandford, R. D., and Znajek, R. L. (1977). “Electromagnetic Extraction of Energy from Kerr Black Holes,” Monthly Notices of the Royal Astronomical Society, 179, 433.
Bohr, N., and Wheeler, J. A. (1939). “The Mechanism of Nuclear Fission,” Physical Review, 56, 426.
Bolton, J. G., Stanley, G. J., and Slee, O. B. (1949). “Positions of Three Discrete Sources of Galactic Radio-Frequency Radiation,” Nature, 164, 101.
Boyer, R. H., and Lindquist, R. W. (1967). “Maximal Analytic Extension of the Kerr Metric,” Journal of Mathematical Physics, 8 , 265.
Braginsky, V. B. (1967). “Classical and Quantum Restrictions on the Detection of Weak Disturbances of a Macroscopic Oscillator,” Zhurnal Eksperimentalnoi i Teoreticheskoi Fizik, 53 , 1434. English translation in Soviet Physics — JETP, 26 , 831 (1968).
Braginsky, V. B. (1977). “The Detection of Gravitational Waves and Quantum Non-disturbtive Measurements,” in Topics in Theoretical and Experimental Gravitation Physics, edited by V. de Sabbata and J. Weber (Plenum, London), p. 105.
Braginsky, V. B., and Khalili, F. Ya. (1992). Quantum Measurements (Cambridge University Press, Cambridge, England).
Braginsky, V. B., Vorontsov, Yu. I., and Khalili, F. Ya. (1978). “Optimal Quantum Measurements in Detectors of Gravitational Radiation,” Pis’ma v Redaktsiyu Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki 27 , 296. English translation in JETP Letters, 27 , 276 (1978).
Braginsky, V. B., Vorontsov, Yu. I., and Thorne, K. S. (1980). “Quantum Nondemolition Measurements,” Science, 209, 547.
Brault, J. W. (1962). “The Gravitational Redshift in the Solar Spectrum,” unpublished doctoral dissertation, Princeton University; available from University Microfilms, Ann Arbor, Michigan.
Brown, A. C., ed. (1978). DROPSHOT: The American Plan for World War III against Russia in 1957 (Dial Press/James Wade, New York).
Bunting, G. (1983). “Proof of the Uniqueness Conjecture for Black Holes,” unpublished Ph.D. dissertation, Department of Mathematics, University of New England, Armidale, N.S.W. Australia.
Burbidge, G. R. (1959). “The Theoretical Explanation of Radio Emission,” in Paris Symposium on Radio Astronomy, edited by R. N. Bracewell (Stanford University Press, Stanford, California).
Candelas, P. (1980). “Vacuum Polarization in Schwarzschild Spacetime,” Physical Review D, 21 ,2185.
Cannon, R. C., Eggleton, P. P.,
![]() ytkow, A. N., and Podsiadlowski, P. (1992). “The Structure and Evolution of Thorne—
ytkow, A. N., and Podsiadlowski, P. (1992). “The Structure and Evolution of Thorne—
![]() ytkow Objects,”
Astrophysical Journal
,
386,
206-214.
ytkow Objects,”
Astrophysical Journal
,
386,
206-214.
Carter, B. (1966). “Complete Analytic Extension of the Symmetry Axis of Kerr’s Solution of Einstein’s Equations,” Physical Review, 141, 1242.
Carter, B. (1968). “Global Structure of the Kerr Family of Gravitational Fields,” Physical Review, 174, 1559.
Carter, B. (1979). “The General Theory of the Mechanical, Electromagnetic and Thermodynamic Properties of Black Holes,” in General Relativity: An Einstein Centenary Survey, edited by S. W. Hawking and W. Israel (Cambridge University Press, Cambridge, England), p. 294.
Caves, C. M., Thorne, K. S., Drever, R. W. P., Sandberg, V. D., and Zimmermann, M. (1980). “On the Measurement of a Weak Classical Force Coupled to a Quantum-Mechanical Oscillator. I. Issues of Principle,” Reviews of Modern Physics, 52 ,341.
Chandrasekhar, S. (1931). “The Maximum Mass of Ideal White Dwarfs,” Astrophysical Journal , 74, 81.
Chandrasekhar, S. (1935). “The Highly Collapsed Configurations of a Stellar Mass (Second Paper),” Monthly Notices of the Royal Astronomical Society, 95 , 207.
Chandrasekhar, S. (1983a). Eddington: The Most Distinguished Astrophysicist of His Time (Cambridge University Press, Cambridge, England).
Chandrasekhar, S. (1983b). The Mathematical Theory of Black Holes (Oxford University Press, New York).
Chandrasekhar, S. (1989). Selected Papers of S. Chandrasekhar. Volume I: Stellar Structure and Stellar Atmospheres (University of Chicago Press, Chicago).
Chandrasekhar, S., and Hartle, J. M. (1982). “On Crossing the Cauchy Horizon of a Reissner-Nordström Black Hole,” Proceedings of the Royal Society of London,
A384, 301.
Christodoulou, D. (1970). “Reversible and Irreversible Transformations in Black-Hole Physics,” Physical Review Letters, 25 , 1596.
Clark, R. W. (1971). Einstein: The Life and Times (World Publishing Co., New York).
Cohen, J. M., and Wald, R. M. (1971). “Point Charge in the Vicinity of a Schwarzschild Black Hole,” Journal of Mathematical Physics, 12 , 1845.
Colgate, S. A., and Johnson, M. H. (1960). “Hydrodynamic Origin of Cosmic Rays,” Physical Review Letters, 5 , 235.
Colgate, S. A., and White, R. H. (1963). “Dynamics of a Supernova Explosion,” Bulletin of the American Physical Society, 8 , 306.
Colgate, S. A., and White, R. H. (1966). “The Hydrodynamic Behavior of Supernova Explosions,” Astrophysical Journal, 143, 626.
Collins, H. M. (1975). “The Seven Sexes: A Study in the Sociology of a Phenomenon, or the Replication of Experiments in Physics,” Sociology, 9 , 205
Collins, H. M. (1981). “Son of Seven Sexes: The Social Destruction of a Physical Phenomenon,” Social Studies of Science (SAGE, London and Beverly Hills), 11 ,33.
Damour, T. (1978). “Black-Hole Eddy Currents,” Physical Review D, 18 , 3598.
Davies, P. C. W. (1975). “Scalar Particle Production in Schwarzschild and Rindler Metrics,” Journal of Physics A, 8 , 609.
de la Cruz, V., Chase, J. E., and Israel, W. (1970). “Gravitational Collapse with Asymmetries,” Physical Review Letters, 24 , 423.
de Sabbata, V., and Weber, J., eds. (1977). Topics in Theoretical and Experimental Gravitation Physics (Plenum, New York).
DeWitt, C., and DeWitt, B. S., eds. (1964). Relativity, Groups, and Topology (Gordon and Breach, New York).
DeWitt, C., and DeWitt, B. S., eds. (1973). Black Holes (Gordon and Breach, New York).
Doroshkevich, A. D., and Novikov, I. D. (1978). “Space-Time and Physical Fields in Black Holes,” Zhurnal Eksperimentalnoi i Teoreticheskii Fiziki, 74 , 3. English translation in Soviet Physics — JETP, 47 , 1 (1978).
Doroshkevich, A. D., Zel’dovich, Ya. B., and Novikov, I. D. (1965). “Gravitational Collapse of Nonsymmetric and Rotating Masses,” Zhurnal Eksperimentalnoi i Teoreticheskii Fiziki, 49 , 170. English translation in Soviet Physics — JETP, 22 , 122 (1966).
Drell, S., and Kapitsa, S., eds. (1991). Sakharov Remembered: A Tribute by Friends and Colleagues (American Institute of Physics, New York).
Drever, R. W. P. (1991). “Fabry–Perot Cavity Gravity-Wave Detectors,” in The Detection of Gravitational Waves, edited by D. Blair (Cambridge University Press, Cambridge, England), p. 306.
Dyson, F. J. (1963). “Gravitational Machines,” in The Search for Extraterrestrial Life, edited by A. G. W. Cameron (W. A. Benjamin, New York), p. 115.
Echeverria, F., Klinkhammer, G., and Thorne, K. S. (1991). “Billiard Balls in Wormhole Spacetimes with Closed Timelike Curves. I. Classical Theory,” Physical Review D, 44, 1077.
ECP-1: Einstein, A. (1987). The Collected Papers of Albert Einstein. Volume 1: The Early Years, 1879–1902, edited by John Stachel (Princeton University Press, Princeton, New Jersey). English translation by Anna Beck in a companion volume of the same title.
ECP-2: Einstein, A. (1989). The Collected Papers of Albert Einstein Volume 2: The Swiss Years: Writings, 1900–1909, edited by John Stachel (Princeton University Press, Princeton, New Jersey). English translation by Anna Beck in a companion volume of the same title.
Eddington, A. S. (1926). The Internal Constitution of the Stars (Cambridge University Press, Cambridge, England).
Eddington, A. S. (1935a). “Relativistic Degeneracy,” Observatory, 58, 37.
Eddington, A. S. (1935b). “On Relativistic Degeneracy,” Monthly Notices of the Royal Astronomical Society, 95, 194.
Einstein, A. (1911). “On the Influence of Gravity on the Propagation of Light,” Annalen der Physik, 35, 898.
Einstein, A. (1915). “The Field Equations for Gravitation,” Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik, 1915, 844.
Einstein, A. (1939). “On a Stationary System with Spherical Symmetry Consisting of Many Gravitating Masses,” Annals of Mathematics, 40, 922.
Einstein, A. (1949). “Autobiographical Notes,” in Albert Einstein: Philosopher-Scientist, edited by Paul A. Schilpp (Library of Living Philosophers, Evanston, Illinois).
Einstein, A., and Maric, M. (1992). Albert Einstein/Mileva Maric: The Love Letters, edited by Jürgen Renn and Robert Schulman (Princeton University Press, Princeton, New Jersey).
Eisenstaedt, J. (1982). “Histoire et Singularités de la Solution de Schwarzschild,” Archive for History of Exact Sciences, 27 , 157.
Eisenstaedt, J. (1991). “De 1’lnfluence de la Gravitation sur la Propagation de la Lumière en Théorie Newtonienne. L’Archéologie des Trous Noirs,” Archive for History of Exact Sciences, 42 , 315.
Epstein, R., and Clark, J. P. A. (1979). “Discussion Session II: Sources of Gravitational Radiation,” in Sources of Gravitational Radiation, edited by L. Smarr (Cambridge University Press, Cambridge, England), p. 477.
Feynman, R. P. (1965). The Character of Physical Law (British Broadcasting Corporation, London; paperback edition: MIT Press, Cambridge, Massachusetts).
Finkelstein, D. (1958). “Past–Future Asymmetry of the Gravitational Field of a Point Particle,” Physical Review, 110 , 965.
Finkelstein, D. (1993). “Misner, Kinks, and Black Holes,” in Directions in General Relativity. Volume 1: Papers in Honor of Charles Misner, edited by B. L. Hu, M. P. Ryan Jr., and C. V. Vishveshwara (Cambridge University Press, Cambridge, England), p. 99.
Flamm, L. (1916). “Beitrage zur Einsteinschen Gravitationstheorie,” Physik Zeitschrift, 17 , 448.
Forward, R. L. (1992). Timemaster. (Tor Books, New York).
Fowler, R. H. (1926). “On Dense Matter,” Monthly Notices of the Royal Astronomical Society, 87 , 114.
Frank, P. (1947). Einstein: His Life and Times (Alfred A. Knopf, New York).
Friedman, H. (1972). “Rocket Astronomy,” Annals of the New York Academy of Sciences, 198, 267.
Friedman, J., and Morris, M. S. (1991). “The Cauchy Problem for the Scalar Wave Equation Is Well Defined on a Class of Spacetimes with Closed Timelike Curves,” Physical Review Letters, 66 , 401.
Friedman, J., Morris, M. S., Novikov, I. D., Echeverria, F., Klinkhammer, G., Thorne, K. S., and Yurtsever, U. (1990). “Cauchy Problem in Spacetimes with Closed Timelike Curves,” Physical Review D, 42 , 1915.
Friedman, J., Papastamatiou, N., Parker, L., and Zhang, H. (1988). “Non-orientable Foam and an Effective Planck Mass for Point-like Fermions,” Nuclear Physics, B309, 533; appendix.
Frolov, V. P. (1991). “Vacuum Polarization in a Locally Static Multiply Connected Spacetime and a Time-Machine Problem,” Physical Review D, 43 , 3878.
Gamow, G. (1937). Structure of Atomic Nuclei and Nuclear Transformations (Clarendon Press, Oxford, England), pp. 234–238.
Gamow, G. (1970). My World Line (Viking Press, New York).
Geroch, R. P. (1967). “Topology in General Relativity,” Journal of Mathematical Physics, 8, 782.
Gertsenshtein, M. E., and Pustovoit, V. I. (1962). “On the Detection of Low-Frequency Gravitational Waves,” Zhurnal Eksperimentalnoi i Teoreticheskoi Fizik , 43 , 605. English translation in Soviet Physics — JETp, 16 , 433 (1963).
Giacconi, R., and Gursky, H., eds. (1974). X-Ray Astronomy (Reidel, Dordrecht, Holland).
Giacconi, R., Gursky, H., Paolini, F. R., and Rossi, B. B. (1962). “Evidence for X-Rays from Sources Outside the Solar System,” Physical Review Letters, 9 , 439.
Gibbons, G. (1979). “The Man Who Invented Black Holes,” New Scientist, 28 , 1101 (29 June).
Gibbons, G. W., and Hawking, S. W. (1977). “Action Integrals and Partition Functions in Quantum Gravity,” Physical Review D, 15 , 2752.
Giffard, R. (1976). “Ultimate Sensitivity Limit of a Resonant Gravitational Wave Antenna Using a Linear Motion Detector,” Physical Review D, 14 , 2478.
Ginzburg, V. L. (1951). “Cosmic Rays as the Source of Galactic Radio Waves,” Doklady Akademii Nauk SSSR, 76 , 377.
Ginzburg, V. L. (1964). “The Magnetic Fields of Collapsing Masses and the Nature of Superstars,” Doklady Akademii Nauk SSSR, 156, 43. English translation in Soviet Physics — Doklady, 9, 329 (1964).
Ginzburg, V. L. (1984). “Some Remarks on the History of the Development of Radio Astronomy,” in The Early Years of Radio Astronomy, edited by W. J. Sullivan (Cambridge University Press, Cambridge, England).
Ginzburg, V. L. (1990). Private communication to K. S. Thorne.
Ginzburg, V. L., and Ozernoy, L. M. (1964). “On Gravitational Collapse of Magnetic Stars,” Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 47 , 1030. English translation in Soviet Physics — JETp, 20 , 689 (1965).
Gleick, J. (1987). Chaos: Making a New Science (Viking/Penguin, New York).
Gödel, K. (1949). “An Example of a New Type of Cosmological Solution of Einstein’s Field Equations of Gravitation,” Reviews of Modern Physics, 21 , 447.
Golovin, I. N. (1973). L V. Kurchatov (Atomizdat, Moscow), 2nd edition. An English translation of the earlier and less complete first edition was published as Academician Igor Kurchatov (Mir Publishers, Moscow, 1969; also, Selbstver-lag Press, Bloomington, Indiana, 1968).
Goodchild, P. (1980). J Robert Oppenheimer, Shatterer of Worlds (British Broadcasting Corporation, London).
Gorelik, G. E. (1991). “ ‘My Anti-Soviet Activities . . .‘ One Year in the Life of L. D. Landau,” Priroda, November issue, p. 93; in Russian.
Gott, J. R. (1991). “Closed Timelike Curves Produced by Pairs of Moving Cosmic Strings: Exact Solutions,” Physical Review Letters, 66, 1126.
Graves, J. C., and Brill, D. R. (1960). “Oscillitory Character of the Reissner-Nordström Metric for an Ideal Charged Wormhole,” Physical Review, 120, 1507.
Greenstein, J. L. (1963). “Red-shift of the Unusual Radio Source: 3C48,” Nature, 197, 1041.
Greenstein, J. L. (1982). Oral history interview by Rachel Prud’homme, February and March 1982, Archives, California Institute of Technology.
Greenstein, J. L., Oke, J. B., and Shipman, H. (1985). “On the Redshift of Sirius B,” Quarterly Journal of the Royal Astronomical Society, 26, 279.
Grishchuk, L. P., Petrov, A. N., and Popova, A. D. (1984). “Exact Theory of the Einstein Gravitational Field in an Arbitrary Background Space-Time,” Communications in Mathematical Physics , 94, 379.
Hall, S. S. (1989). “The Man Who Invented Time Travel: The Astounding World of Kip Thorne,” California, October, p. 68.
Hanni, R. S., and Ruffini, R. (1973). “Lines of Force of a Point Charge Near a Schwarzschild Black Hole,” Physical Review D, 8, 3259.
Harrison, B. K., Thorne, K. S., Wakano, M., and Wheeler, J. A. (1965). Gravitation Theory and Gravitational Collapse (University of Chicago Press, Chicago).
Harrison, B. K., Wakano, M., and Wheeler, J. A. (1958). “Matter–Energy at High Density: End Point of Thermonuclear Evolution,” in La Structure et l’Evolution de l’Univers, Onzième Conseil de Physique Solvay (Stoops, Brussels), p. 124.
Hartle, J. B., and Sabbadini, A. G. (1977). “The Equation of State and Bounds on the Mass of Nonrotating Neutron Stars,” Astrophysical Journal, 213, 831.
Hawking, S. W. (1971a). “Gravitationally Collapsed Objects of Very Low Mass,” Monthly Notices of the Royal Astronomical Society, 152, 75.
Hawking, S. W. (1971b). “Gravitational Radiation from Colliding Black Holes,” Physical Review Letters, 26 , 1344.
Hawking, S. W. (1972). “Black Holes in General Relativity,” Communications in Mathematical Physics, 25 , 152.
Hawking, S. W. (1973). “The Event Horizon,” in Black Holes, edited by C. DeWitt and B. S. DeWitt (Gordon and Breach, New York), p. 1.
Hawking, S. W. (1974). “Black Hole Explosions?” Nature, 248, 30. Hawking, S. W. (1975). “Particle Creation by Black Holes,” Communications in Mathematical Physics, 43, 199.
Hawking, S. W. (1976). “Black Holes and Thermodynamics,” Physical Review D, 13, 191.
Hawking, S. W. (1987). “Quantum Cosmology,” in 300 Years of Gravitation, edited by S. W. Hawking and W. Israel (Cambridge University Press, Cambridge, England), p. 631.
Hawking, S. W. (1988). A Brief History of Time (Bantam Books, Toronto, New York). Hawking, S. W. (1992a). “The Chronology Protection Conjecture,” Physical Review D, 46 , 603.
Hawking, S. W. (1992b). “Evaporation of Two-Dimensional Black Holes,” Physical Review Letters, 69 , 406.
Hawking, S. W., and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time (Cambridge University Press, Cambridge, England).
Hawking, S. W., and Hartle, J. B. (1972). “Energy and Angular Momentum Flow into a Black Hole,” Communications in Mathematical Physics, 27, 283.
Hawking, S. W., and Penrose, R. (1970). “The Singularities of Gravitational Collapse and Cosmology,” Proceedings of the Royal Society of London, A314, 529.
Hey, J. S. (1973). The Evolution of Radio Astronomy (Neale Watson Academic Publications, Inc., New York).
Hirsh, R. F. (1979). “Science, Technology, and Public Policy: The Case of X-Ray Astronomy, 1959 to 1972,” unpublished Ph.D. dissertation, University of Wisconsin–Madison; available from University Microfilms, Ann Arbor, Michigan.
Hiscock, W. A., and Konkowski, D. A. (1982). “Quantum Vacuum Energy in Taub–NUT (Newman–Unti–Tamburino)-Type Cosmologies,” Physical Review D, 6 , 1225.
Hoffman, B. (1972). In collaboration with H. Dukas, Albert Einstein: Creator and Rebel (Viking, New York).
Imshennik, V. S., and Nadezhin, D. K. (1964). “Gas Dynamical Model of a Type 11 Supernova Outburst,” Astronomicheskii Zhurnal 41, 829. English translation in Soviet Astronomy — AJ, 8 , 664 (1965).
Israel, W. (1967). “Event Horizons in Static Vacuum Spacetimes,” Physical Review, 164, 1776.
Israel, W. (1986). “Third Law of Black Hole Dynamics—A Formulation and Proof,” Physical Review Letters, 57 , 397.
Israel, W. (1987). “Dark Stars: The Evolution of an Idea,” in 300 Years of Gravitation, edited by S. W. Hawking and W. Israel (Cambridge University Press, Cambridge, England), p. 199.
Israel, W. (1990). Letter to K. S. Thorne, dated 28 May 1990, commenting on the semifinal draft of this book.
Jansky, K. (1932). “Directional Studies of Atmospherics at High Frequencies,” Proceedings of the Institute of Radio Engineers, 20 , 1920.
Jennison, R. C., and Das Gupta, M. K. (1953). “Fine Structure of the Extra-terrestrial Radio Source Cygnus 1,” Nature, 172, 996.
Kellermann, K., and Sheets, B. (1983). Serendipitous Discoveries in Radio Astronomy (National Radio Astronomy Observatory, Green Bank, West Virginia).
Kerr, R. P. (1963). “Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics,” Physical Review Letters, 11, 237.
Kevles, D. J. (1971). The Physicists (Random House, New York).
Khalatnikov, I. M., ed. (1988). Vospominaniya o L. D. Landau (Nauka, Moscow). English translation: Landau, the Physicist and the Man: Recollections of L. D. Landau (Pergamon Press, Oxford, England, 1989).
Khalatnikov, I. M., and Lifshitz, E. M. (1970). “The General Cosmological Solution of the Gravitational Equations with a Singularity in Time,” Physical Review Letters, 24, 76.
Kiepenheuer, K. O. (1950). “Cosmic Rays as the Source of General Galactic Radio Emission,” Physical Review, 79 , 738.
Kim, S.-W., and Thorne, K. S. (1991). “Do Vacuum Fluctuations Prevent the Creation of Closed Timelike Curves?” Physical Review D, 43, 3939.
Klauder, J. R., ed. (1972). Magic without Magic: John Archibald Wheeler (W. H. Freeman, San Francisco).
Kruskal, M. D. (1960). “Minimal Extension of the Schwarzschild Metric,” Physical Review, 119, 1743.
Kuhn, T. (1962). The Structure of Scientific Revolutions (University of Chicago Press, Chicago).
Landau, L. D. (1932). “On the Theory of Stars,” Physikalische Zeitschrift Sowjetunion, 1 , 285.
Landau, L. D. (1938). “Origin of Stellar Energy,” Nature, 141, 333.
Landau, L. D., and Lifshitz, E. M. (1962). Teoriya Polya (Gosudarstvennoye Izdatel’stvo Fiziko-Matematicheskoi Literaturi, Moscow), Section 108. English translation: The Classical Theory of Fields (Pergamon Press, Oxford, England, 1962), Section 110.
Laplace, P. S. (1796). Exposition du Système du Monde. Volume II: Des Mouvements Réels des Corps Célestes (Paris). Published in English as The System of the World (W. Flint, London, 1809).
Laplace, P. S. (1799). “Proof of the Theorem, that the Attractive Force of a Heavenly Body Could Be So Large, that Light Could Not Flow Out of It,” Allgemeine Geographische Ephemeriden, verfasset von Einer Gesellschaft Gelehrten. 8vo Weimer, IV, Bd I St. English translation in Appendix A of Hawking and Ellis (1973).
Lifshitz, E. M., and Khalatnikov, I. M. (1960). “On the Singularities of Cosmological Solutions of the Gravitational Equations. I.” Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki 39 , 149. English translation in Soviet Physics — JETP, 12 , 108 and 558 (1961).
Lifshitz, E. M., and Khalatnikov, I. M. (1963). “Investigations in Relativistic Cosmology,” Advances in Physics, 12 , 185.
Livanova, A. (1980). Landau: A Great Physicist and Teacher (Pergamon Press, Oxford, England).
Longair, M. S., Ryle, M., and Scheuer, P. A. G. (1973). “Models of Extended Radio Sources,” Monthly Notices of the Royal Astronomical Society, 164, 243.
Lorentz, H. A., Einstein, A., Minkowski, H., and Weyl, H. (1923). The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity (Dover, New York).
Lynden-Bell, D. (1969). “Galactic Nuclei as Collapsed Old Quasars,” Nature, 223 , 690.
Lynden-Bell, D. (1978). “Gravity Power,” Physica Scripta, 17 , 185.
Mazur, P. (1982). “Proof of Uniqueness of the Kerr–Newman Black Hole Solution,” Journal of Physics A, 15 , 3173.
May, M. M., and White, R. H. (1965). “Hydrodynamical Calculation of General Relativistic Collapse,” Bulletin of the American Physical Society, 10 , 15.
May, M. M., and White, R. H. (1966). “Hydrodynamic Calculations of General Relativistic Collapse,” Physical Review, 141, 1232.
Medvedev, Z. A. (1978). Soviet Science (W. W. Norton, New York).
Medvedev, Z. A. (1979). Nuclear Disaster in the Urals (W. W. Norton, New York).
Michell, J. (1784). “On the Means of Discovering the Distance, Magnitude, Etc., of the Fixed Stars, in Consequence of the Diminution of Their Light, in Case Such a Diminution Should Be Found to Take Place in Any of Them, and Such Other Data Should Be Procured from Observations, as Would Be Further Necessary for That Purpose,” in Philosophical Transactions of the Royal Society of London, 74 , 35; presented to the Royal Society on 27 November 1783.
Michelson, P. F., and Taber, R. C. (1984). “Can a Resonant-Mass Gravitational-Wave Detector Have Wideband Sensitivity?” Physical Review D, 29 , 2149.
Misner, C. W. (1969). “Mixmaster Universe,” Physical Review Letters, 22 , 1071.
Misner, C. W., Thorne, K. S., and Wheeler, J. A. (1973). Gravitation (W. H. Freeman, San Francisco).
Mitton, S., and Ryle, M. (1969). “High Resolution Observations of Cygnus A at 2.7 GHz and 5 GHz,” Monthly Notices of the Royal Astronomical Society, 146, 221.
Morris, M. S., and Thorne, K. S. (1988). “Wormholes in Spacetime and Their Use for Interstellar Travel: A Tool for Teaching General Relativity,” American Journal of Physics, 56 , 395.
Morris, M. S., Thorne, K. S., and Yurtsever, U. (1988). “Wormholes, Time Machines, and the Weak Energy Condition,” Physical Review Letters, 61, 1446.
Moss, G. E., Miller, L. R., and Forward, R. L. (1971). “Photon Noise Limited Laser Transducer for Gravitational Antenna,” Applied Optics, 10 , 2495.
MTW: Misner, Thorne, and Wheeler (1973).
Newman, E. T., Couch, E., Chinnapared, K., Exton, A., Prakash, A., and Torrence, R. (1965). “Metric of a Rotating, Charged Mass,” Journal of Mathematical Physics, 6 , 918.
Novikov, I. D. (1963). “The Evolution of the Semi-Closed World,” Astronomicheskii Zhurnal, 40 , 772. English translation in Soviet Astronomy — AJ, 7 , 587 (1964).
Novikov, I. D. (1966). “Change of Relativistic Collapse into Anticollapse and Kinematics of a Charged Sphere,” Pis’ma v Redaktsiyu Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 3 , 223. English translation in JETP Letters, 3 , 142 (1966).
Novikov, I. D. (1969). “Metric Perturbations When Crossing the Schwarzschild Sphere,” Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 57 , 949. English translation in Soviet Physics—JETP, 30 , 518 (1970).
Novikov, I. D., Polnarev, A. G., Starobinsky, A. A., and Zel’dovich, Ya. B. (1979). “Primordial Black Holes,” Astronomy and Astrophysics, 80 , 104.
Novikov, I. D., and Zel’dovich, Ya. B. (1966). “Physics of Relativistic Collapse,” Supplemento al Nuovo Cimento, 4 , 810; Addendum 2.
Oppenheimer, J. R., and Serber, R. (1938). “On the Stability of Stellar Neutron Cores,” Physical Review, 54 , 608.
Oppenheimer, J. R., and Snyder, H. (1939). “On Continued Gravitational Contraction,” Physical Review, 56 , 455.
Oppenheimer, J. R., and Volkoff, G. (1939). “On Massive Neutron Cores,” Physical Review, 54 , 540.
Ori, A. (1991). “The Inner Structure of a Charged Black Hole: An Exact Mass Inflation Solution,” Physical Review Letters, 67 , 789.
Ori, A. (1992). “Structure of the Singularity Inside a Realistic Rotating Black Hole,” Physical Review Letters, 68 , 2117.
Page, D. N. (1976). “Particle Emission Rates from a Black Hole,” Physical Review D, 13 , 198, and 14 , 3260.
Page, D. N., and Hawking, S. W. (1975). “Gamma Rays from Primordial Black Holes,” Astrophysical Journa4 206, 1.
Pagels, H. (1982). The Cosmic Code (Simon and Schuster, New York).
Pais, A. (1982). “Subtle Is the Lord . . .” The Science and the Life of Albert Einstein (Oxford University Press, Oxford, England).
Penrose, R. (1965). “Gravitational Collapse and Spacetime Singularities,” Physical Review Letters, 14, 57.
Penrose, R. (1968). “The Structure of Spacetime,” in Battelle Rencontres: 1967 Lectures in Mathematics and Physics, edited by C. M. DeWitt and J. A. Wheeler (Benjamin, New York), p. 565.
Penrose, R. (1969). “Gravitational Collapse: The Role of General Relativity,” Rivista Nuovo Cimento, 1, 252.
Penrose, R. (1989). The Emperor’s New Mind (Oxford University Press, New York), pp. 419-421.
Phinney, E. S. (1989). “Manifestations of a Massive Black Hole in the Galactic Center,” in The Center of the Galaxy: Proceedings of IAU Symposium 136, edited by M. Morris (Reidel, Dordrecht, Holland), p. 543.
Pimenov, R. I. (1968). Prostranstva Kinimaticheskovo Tipa [Seminars in Mathematics ], Vol. 6 (V. A. Steklov Mathematical Institute, Leningrad). English translation: Kinematic Spaces (Consultants Bureau, New York, 1970).
Podurets, M. A. (1964). “The Collapse of a Star with Back Pressure Taken Into Account,” Doklady Akademi Nauk, 154, 300. English translation in Soviet Physics—Doklady, 9 , 1 (1964).
Poisson, E., and Israel, W. (1990). “Internal Structure of Black Holes,” Physical Review D, 41, 1796.
Press, W. H. (1971). “Long Wave Trains of Gravitational Waves from a Vibrating Black Hole,” Astrophysical Journal Letters, 170, 105.
Press, W. H., and Teukolsky, S. A. (1973). “Perturbations of a Rotating Black Hole. II. Dynamical Stability of the Kerr Metric,” Astrophysical Journal 185, 649.
Price, R. H. (1972). “Nonspherical Perturbations of Relativistic Gravitational Collapse,” Physical Review D, 5 , 2419 and 2439.
Price, R. H., and Thome, K. S. (1988). “The Membrane Paradigm for Black Holes,” Scientific American, 258 (No. 4), 69.
Rabi, I. I., Serber, R., Weisskopf, V. F., Pais, A., and Seaborg, G. T. (1969). Oppenheimer (Scribners, New York).
Reber, G. (1940). “Cosmic Static,” Astrophysical Journal, 91 , 621.
Reber, G. (1944). “Cosmic Static,” Astrophysical Journal, 100, 279.
Reber, G. (1958). “Early Radio Astronomy at Wheaton, Illinois,” Proceedings of the Institute of Radio Engineers, 46 , 15.
Rees, M. (1971). “New Interpretation of Extragalactic Radio Sources,” Nature, 229 , 312 and 510.
Renn, J., and Schulman, R. (1992). Introduction to Albert Einstein/Mileva Maric: The Love Letters, edited by Jürgen Renn and Robert Schulman (Princeton University Press, Princeton, New Jersey).
Rhodes, R. (1986). The Making of the Atomic Bomb (Simon and Schuster, New York).
Ritus V. 1. (1990). “If Not I, Then Who?” Priroda, August issue. English translation in Drell and Kapitsa, eds. (1991).
Robinson, I., Schild, A., and Schucking, E. L., eds. (1965). Quasi-Stellar Sources and Gravitational Collapse (University of Chicago Press, Chicago).
Romanov, Yu. A. (1990). “The Father of the Soviet Hydrogen Bomb,” Priroda, August issue. English translation in Drell and Kapitsa, eds. (1991).
Royal, D. (1969). The Story of J. Robert Oppenheimer (St. Martin’s Press, New York).
Sagan, C. (1985). Contact (Simon and Schuster, New York).
Sakharov, A. (1990). Memoirs (Alfred A. Knopf, New York).
Salpeter, E. E. (1964). “Accretion of Interstellar Matter by Massive Objects,” Astrophysical Journal 140, 796.
Schaffer, S. (1979). “John Michell and Black Holes,” Journal for the History of Astronomy, 10 , 42.
Schmidt, M. (1963). “3C273: A Star-like Object with Large Red-shift,” Nature, 197, 1040.
Schwarzschild, K. (1916a). “Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie,” Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik, 1916 , 189.
Schwarzschild, K. (1916b). “Uber das Gravitationsfeld einer Kugel aus inkompressibier Flussigkeit nach der Einsteinschen Theorie,” Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik, 1916 , 424.
Seelig, C. (1956). Albert Einstein: A Documentary Biography (Staples Press, London), p. l04.
Serber, R. (1969). “The Early Years,” in Rabi et al. (1969); also published in Physics Today, October 1967, p. 35.
Shapiro, S. L., and Teukolsky, S. A. (1983). Black Holes, White Dwarfs, and Neutron Stars (Wiley, New York).
Shapiro, S. L., and Teukolsky, S. A. (1991). “Formation of Naked Singularities—The Violation of Cosmic Censorship,” Physical Review Letters, 66 , 994.
Smart, W. M. (1953). Celestial Mechanics (Longmans, Green and Co., London), Section 19.03.
Smith, A. K., and Weiner, C. (1980). Robert Oppenheimen: Letters and Recollections (Harvard University Press, Cambridge, Massachusetts).
Smith, H. J. (1965). “Light Variations of 3C273,” in Quasi-Stellar Sources and Gravitational Collapse, edited by I. Robinson, A. Schild, and E. L. Schucking (University of Chicago Press, Chicago), p. 221.
Solvay (1958). Onzieme Conseil de Physique Solvay, La Structure et l’Evolution de l’Univers (Editions R. Stoops, Brussels).
Stoner, E. C. (1930). “The Equilibrium of Dense Stars,” Philosophical Magazine, 9 , 944.
Strove, O., and Zebergs, V. (1962). Astronomy of the 20th Century (Macmillan, New York).
Sullivan, W. J., ed. (1982). Classics in Radio Astronomy (Reidel, Dordrecht, Holland).
Sullivan, W. J., ed. (1984). The Early Years of Radio Astronomy (Cambridge University Press, Cambridge, England).
Sunyaev, R. A. (1972). “Variability of X Rays from Black Holes with Accretion Disks,” Astronomicheskii Zhurnal 49 , 1153. English translation in Soviet Astronomy—AJ, 16 , 941 (1973).
Taylor, E. F., and Wheeler, J. A. (1992). Spacetime Physics: Introduction to Special Relativity (W. H. Freeman, San Francisco).
Teller, E. (1955). “The Work of Many People,” Science, 121, 268.
Teukolsky, S. A. (1972). “Rotating Black Holes: Separable Wave Equations for Gravitational and Electromagnetic Perturbations,” Physical Review Letters, 29 ,1115.
Thorne, K. S. (1967). “Gravitational Collapse,” Scientific American, 217 (No. 5), 96.
Thorne, K. S. (1972). “Nonspherical Gravitational Collapse—A Short Review,” in Magic without Magic: John Archibald Wheeler, edited by J. R. Klauder (W. H. Freeman, San Francisco), p. 231.
Thorne, K. S. (1974). “The Search for Black Holes,” Scientific American, 231 (No. 6), 32.
Thorne, K. S. (1987). “Gravitational Radiation,” in 300 Years of Gravitation, edited by S. W. Hawking and W. Israel (Cambridge University Press, Cambridge, England), p. 330.
Thorne, K. S. (1991). “An American’s Glimpses of Sakharov,” Priroda, May issue; in Russian. English translation in Drell and Kapitsa, eds. (1991), p. 74.
Thorne, K. S. (1993). “Closed Timelike Curves,” in General Relativity and Gravitation 1992, edited by R. J. Gleiser, C. N. Kozameh, and D. M. Moreschi (Institute of Physics Publishing, Bristol, England), p. 295.
Thorne, K. S., Drever, R. W. P., Caves, C. M., Zimmermann, M., and Sandberg, V. D. (1978). “Quantum Nondemolition Measurements of Harmonic Oscillators,” Physical Review Letters, 40 , 667.
Thorne, K. S., Price, R. H., and Macdonald, D. A., eds. (1986). Black Holes: The Membrane Paradigm (Yale University Press, New Haven, Connecticut).
Thorne, K. S., and Zurek, W. (1986). “John Archibald Wheeler: A Few Highlights of His Contributions to Physics,” Foundations of Physics, 16, 79.
Thorne, K. S., and Zytkow, A. N. (1977). “Stars with Degenerate Neutron Cores. I. Structure of Equilibrium Models,” Astrophysical Journal, 212, 832.
Tipler, F. J. (1976). “Causality Violation in Asymptotically Flat Space-Times,” Physical Review Letters, 37 , 879.
Tolman, R. C. (1939). “Static Solutions of Einstein’s Field Equations for Spheres of Fluid,” Physical Review, 55 , 364.
Tolman, R. C. (1948). The Richard Chace Tolman Papers, archived in the California Institute of Technology Archives.
Trimble, V. L., and Thorne, K. S. (1969). “Spectroscopic Binaries and Collapsed Stars,” Astrophysical Journal, 56 , 1013.
Uhuru (1981). “Proceedings of the Uhuru Memorial Symposium: The Past, Present, and Future of X-Ray Astronomy,” Journal of the Washington Academy of Sciences, 71 (No. 1).
Unruh, W. G. (1976). “Notes on Black-Hole Evaporation,” Physical Review D, 14 , 870.
Unruh, W. G., and Wald, R. M. (1982). “Acceleration Radiation and the Generalized Second Law of Thermodynamics,” Physical Review D, 25 , 942.
Unruh, W. G., and Wald, R. M. (1984). “What Happens When an Accelerating Observer Detects a Rindler Particle,” Physical Review D, 29 , 1047.
USAEC [United States Atomic Energy Commission] (1954). In the Matter of J. Robert Oppenheimer; Transcript of Hearing before Personnel Security Board, Washington, D.C., April 12, 1954, through May 6, 1954 (U.S. Government Printing Office, Washington, D.C.).
van Stockum, W. J. (1937). “The Gravitational Field of a Distribution of Particles Rotating about an Axis of Symmetry,” Proceedings of the Royal Society of Edinburgh, 57 , 135.
Wald, R. M. (1977). “The Back Reaction Effect in Particle Creation in Curved Space-time,” Communications in Mathematical Physics, 54 , 1.
Wald, R. M., and Yurtsever, U. (1991). “General Proof of the Averaged Null Energy Condition for a Massless Scalar Field in Two-Dimensional Curved Space-time,” Physical Review D, 44 , 403.
Wali, K. C. (1991). Chandra: A Biography of S. Chandrasekhar (University of Chicago Press, Chicago).
Washington (1954). “Washington Conference on Radio Astronomy—1954,” Journal of Geophysical Research, 59 , 1–204.
Weber, J. (1953). “Amplification of Microwave Radiation by Substances Not in Thermal Equilibrium,” Transactions of the IEEE, PG Electron Devices— 3, 1 (June).
Weber, J. (1960). “Detection and Generation of Gravitational Waves,” Physical Review, 117, 306.
Weber, J. (1961). General Relativity and Gravitational Waves (Wiley–Interscience, New York).
Weber, J. (1964). Unpublished research notebooks; also documented in Robert Forward’s unpublished Personal Journal No. C1338, page 66, 13 September 1964.
Weber, J. (1969). “Evidence for Discovery of Gravitational Radiation,” Physical Review Letters, 22 , 1320.
Weiss, R. (1972). “Electromagnetically Coupled Broadband Gravitational Antenna,” Quarterly Progress Report of the Research Laboratory of Electronics, M.I.T., 105, 54.
Wheeler, J. A. (1955). “Geons,” Physical Review, 97 , 511. Reprinted in Wheeler (1962), p. 131.
Wheeler, J. A. (1957). “On the Nature of Quantum Geometrodynamics,” Annals of Physics, 2, 604.
Wheeler, J. A. (1960). “Neutrinos, Gravitation and Geometry,” in Proceedings of the International School of Physics, “Enrico Ferm,” Course XI (Zanichelli, Bologna). Reprinted in Wheeler (1962), p. 1.
Wheeler, J. A. (1962). Geometrodynamics (Academic Press, New York).
Wheeler, J. A. (1964a). “The Superdense Star and the Critical Nucleon Number,” in Gravitation and Relativity, edited by H. Y. Chiu and W. F. Hoffman (Benjamin, New York), p. 10.
Wheeler, J. A. (1964b). “Geometrodynamics and the Issue of the Final State,” in Relativity, Groups, and Topology, edited by C. DeWitt and B. S. DeWitt (Gordon and Breach, New York), p. 315.
Wheeler, J. A. (1968). “Our Universe: The Known and the Unknown,” American Scientist, 56 , 1.
Wheeler, J. A. (1979). “Some Men and Moments in the History of Nuclear Physics: The Interplay of Colleagues and Motivations,” in Nuclear Physics in Retrospect, edited by Roger H. Stuewer (University of Minnesota, Minneapolis).
Wheeler, J. A. (1985). Letter to K. S. Thorne dated 3 December.
Wheeler, J. A. (1988). Notebooks in which Wheeler recorded his research work and ideas as they developed; now archived at the American Philosophical Society Library, Philadelphia, Pennsylvania.
Wheeler, J. A. (1990). A Journey into Gravity and Spacetime (Scientific American Library, New York).
Whipple, F. L., and Greenstein, J. L. (1937). “On the Origin of Interstellar Radio Disturbances,” Proceedings of the National Academy of Sciences, 23 , 177.
White, T. H. (1939). The Once and Future King (Collins, London), Chapter 13 of Part I, “The Sword in the Stone.”
Will, C. M. (1986). Was Einstein Right? (Basic Books, New York).
York, H. (1976). The Advisors: Oppenheimer, Teller and the Superbomb (W. H. Freeman, San Francisco).
Zel’dovich, Ya. B. (1962). “Semi-closed Worlds in the General Theory of Relativity,” Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki 43 , 1037. English translation in Soviet Physics—JETP, 16 , 732 (1963).
Zel’dovich, Ya. B. (1964). “The Fate of a Star and the Evolution of Gravitational Energy upon Accretion,” Doklady Akademii Nauk, 155 , 67. English translation in Soviet Physics — Doklady, 9, 195 (1964).
Zel’dovich, Ya. B. (1971). “The Generation of Waves by a Rotating Body,” Pis’ma v Redaktsiyu Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 14 , 270. English translation in JETP Letters, 14 , 180 (1971).
Zel’dovich, Ya. B. (1985). Collected Works: Particles, Nuclei, and the Universe (Nauka, Moscow); in Russian. English translation: Selected Works of Yakov Borisovich Zel’dovich Volume II: Particles, Nuclei, and the Universe (Princeton University Press, Princeton, 1993).
Zel’dovich, Ya. B., and Guseinov, O. Kh. (1965). “Collapsed Stars in Binaries,” Astrophysical Journal, 144 , 840.
Zel’dovich, Ya. B., and Khariton, Yu. B. (1939). “On the Issue of a Chain Reaction Based on an Isotope of Uranium,” Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 9 , 1425; see also the follow-up papers by the same authors in the same journal, 10 , 29 (1940) and 10 , 477 (1940). Reprinted as the first three papers in Volume II of Zel’dovich’s collected works, Zel’dovich (1985).
Zel’dovich, Ya. B., and Novikov, I. D. (1964). “Relativistic Astrophysics, Part I,” Uspekhi Fizicheskikh Nauk, 84 , 877. English translation in Soviet Physics — Uspekhi, 7 , 763 (1965).
Zel’dovich, Ya. B., and Novikov, I. D. (1965). “Relativistic Astrophysics, Part II,” Uspekhi Fizicheskikh Nauk, 86 , 447. English translation in Soviet Physics — Uspekhi, 8 , 522 (1966).
Zel’dovich, Ya. B., and Starobinsky, A. A. (1971). “Particle Production and Vacuum Polarization in an Anisotropic Gravitational Field,” Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 61 , 2161. English translation in Soviet Physics — JETP, 34, 1159 (1972).
Znajek, R. (1978). “The Electric and Magnetic Conductivity of a Kerr Hole,” Monthly Notices of the Royal Astronomical Society, 185 , 833.
Zwicky, F. (1935). “Stellar Guests,” Scientific Monthly, 40 , 461.
Zwicky, F. (1939). “On the Theory and Observation of Highly Collapsed Stars,” Physical Review, 55 , 726.