13
in which physicists, wrestling with Einstein’s equation,
seek the secret of what is inside a black hole:
a route into another universe?
a singularity with infinite tidal gravity?
the end of space and time, and birth of quantum foam?
Singularities and Other Universes
W hat is inside a black hole?
How can we know, and why should we care? No signal can ever emerge from the hole to tell us the answer. No intrepid explorer who might enter the hole to find out can ever come back and tell us, or ever transmit the answer to us. Whatever may be in the hole’s core can never reach out and influence our Universe in any way.
Human curiosity is hardly satisfied by such replies. Especially not when we have tools that can tell us the answer: the laws of physics.
John Archibald Wheeler taught us the importance of the quest to understand a black hole’s core. In the 1950s he posed “the issue of the final state” of gravitational implosion as a holy grail for theoretical physics, one that might teach us details of the “fiery marriage” of general relativity with quantum mechanics. When J. Robert Oppenheimer insisted that the final state is hidden from view by a horizon, Wheeler resisted (Chapter 6 )—not least, I suspect, because of his anguish at losing the possibility to see the fiery marriage in action from outside the horizon.
After accepting the horizon, Wheeler retained his conviction that understanding the hole’s core was a holy grail worth pursuing. Just as struggling to understand the evaporation of black holes has helped us to discover a partial marriage of quantum mechanics with general relativity (Chapter 12 ), so struggling to understand a black hole’s core might help us to discover the full marriage; it might lead us to the full laws of quantum gravity. And perhaps the nature of the core will hold the keys to other mysteries of the Universe: There is a similarity between the “big crunch” implosion in which, eons hence, our Universe might die, and the implosion of the star that creates a black hole’s core. By coming to grips with the one, we might learn about the other.
For thirty-five years physicists have pursued Wheeler’s holy grail, but with only modest success. We do not yet know for certain what inhabits a hole’s core, and the struggle to understand has not yet taught us with clarity the laws of quantum gravity. But we have learned much—not least that whatever is inside a black hole’s core is indeed intimately connected with the laws of quantum gravity.
This chapter describes a few of the more interesting twists and turns in the quest for Wheeler’s holy grail, and where the quest has led thus far.
T he first, tentative answer to “What is inside a black hole?” Came from J. Robert Oppenheimer and Hartland Snyder, in their classic 1939 calculation of the implosion of a spherical star (Chapter 6 ). Although the answer was contained in the equations they published, Oppenheimer and Snyder chose not to discuss it. Perhaps they feared it would only add fuel to the controversy over their prediction that the imploding star “cuts itself off from the rest of the Universe” (that is, forms a black hole). Perhaps Oppenheimer’s innate scientific conservatism, his unwillingness to speculate, kept them quiet. Whatever the reason, they said nothing. But their equations spoke.
After creating a black-hole horizon around itself, their equations said, the spherical star continues imploding, inexorably, to infinite density and zero volume, whereupon it creates and merges into a spacetime singularity.
A singularity is a region where—according to the laws of general relativity—the curvature of spacetime becomes infinitely large, and spacetime ceases to exist. Since tidal gravity is a manifestation of spacetime curvature (Chapter 2 ), a singularity is also a region of infinite tidal gravity, that is, a region where gravity stretches all objects infinitely along some directions and squeezes them infinitely along others.
One can conceive of a variety of different kinds of spacetime singularities, each with its own peculiar form of tidal stretch and squeeze, and we shall meet several different kinds in this chapter.
The singularity predicted by the Oppenheimer–Snyder calculations is a very simple one. Its tidal gravity has essentially the same form as the Earth’s or Moon’s or Sun’s; that is, the same form as the tidal gravity that creates the tides on the Earth’s oceans (Box 2.5): The singularity stretches all objects radially (in the direction toward and away from itself), and squeezes all objects transversely.
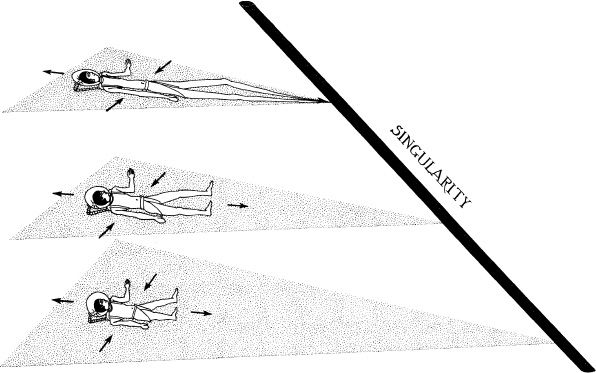
Imagine an astronaut falling feet first into the kind of black hole described by Oppenheimer and Snyder’s equations. The larger the hole, the longer he can survive, so for maximum longevity, let the hole be among the largest that inhabit the cores of quasars (Chapter 9 ): 10 billion solar masses. Then the falling astronaut crosses the horizon and enters the hole about 20 hours before his final death, but as he enters, he is still too far from the singularity to feel its tidal gravity. As he continues to fall faster and faster, coming closer and closer to the singularity, the tidal gravity grows stronger and stronger until, just 1 second before the singularity, he begins to feel it stretching his feet and head apart and squeezing him from the sides (bottom picture in Figure 13.1). At first, the stretch and squeeze are only mildly annoying, but they continue to grow until, a few hundredths of a second before the singularity (middle picture), they get so strong that his bones and flesh can no longer resist. His body comes apart and he dies. In the last hundredth second, the stretch and squeeze continue mounting, and as he reaches the singularity, they become infinitely strong, first at his feet, then at his trunk, then at his head; his body gets infinitely distended; and then, according to general relativity, he merges with and becomes part of the singularity.
It is utterly impossible for the astronaut to move on through the singularity and come out the other side because, according to general relativity, there is no “other side.” Space, time, and spacetime cease to exist at the singularity. The singularity is a sharp edge, much like the edge of a sheet of paper. There is no paper beyond its edge; there is no spacetime beyond the singularity. But there the similarity ends. An ant on the paper can go right up to the edge and then back away, but nothing can back away from the singularity; all astronauts, particles, waves, whatever, that hit it are instantaneously destroyed, according to Einstein’s general relativistic laws.

13.1 Spacetime diagram depicting the feet-first fall of an astronaut into the singularity at a black hole’s center, according to the Oppenheimer–Snyder calculations. As in all previous spacetime diagrams (for example, Figure 6.7), one spatial dimension is missing; that is why the astronaut looks two-dimensional rather than three-dimensional. The singularity is tilted in this diagram, in contrast to its vertical position in Figure 6.7 and Box 12.1, because the time plotted upward and the space plotted horizontally here are different from there. Here they are the astronaut’s own time and space; there they were Finkelstein’s.
The mechanism of destruction is not fully clear in Figure 13.1, because the figure ignores the curvature of space. In fact, as the astronaut’s body reaches the singularity, it gets stretched out to truly infinite length and squashed transversely to truly zero size. The extreme curvature of space near the singularity permits him to become infinitely long without shoving his head out through the hole’s horizon. His head and feet are both pulled into the singularity, but they are pulled in infinitely far apart.
Not only is an astronaut stretched and squeezed infinitely at the singularity, according to the Oppenheimer–Snyder equations; all forms of matter are infinitely stretched and squeezed—even an individual atom; even the electrons, protons, and neutrons that make up atoms; even the quarks that make up protons and neutrons.
Is there any way for the astronaut to escape this infinite stretch and squeeze? No, not after he has crossed the horizon. Everywhere inside the horizon, according to the Oppenheimer–Snyder equations, gravity is so strong (spacetime is so strongly warped) that time itself (every-one’s time) flows into the singularity. 1 Since the astronaut, like anyone else, must move inexorably forward in time, he is driven with the flow of time into the singularity. No matter what he does, no matter how he blasts his rocket engines, the astronaut cannot avoid the singularity’s infinite stretch and squeeze.
W henever we physicists see our equations predict something infinite, we become suspicious of the equations. Almost nothing in the real Universe ever gets truly infinite (we think). Therefore, an infinity is almost always a sign of a mistake.
The singularity’s infinite stretch and squeeze was no exception. Those few physicists who studied Oppenheimer and Snyder’s publication during the 1950s and early 1960s agreed unanimously that something was wrong. But there the unanimity stopped.
One group, led vigorously by John Wheeler, identified the infinite stretch and squeeze as an unequivocal message that general relativity fails inside a black hole, at the endpoint of stellar implosion. Quantum mechanics should prevent tidal gravity from becoming truly infinite there, Wheeler asserted; but how? To learn the answer, Wheeler argued, would require marrying the laws of quantum mechanics with the laws of tidal gravity, that is, with Einstein’s general relativistic laws of curved spacetime. The progeny of that marriage, the laws of quantum gravity, must govern the singularity, Wheeler claimed; and these new laws might create new physical phenomena inside the black hole, phenomena unlike any we have ever met.
A second group, led by Isaac Markovich Khalatnikov and Evgeny Michailovich Lifshitz (members of Lev Landau’s Moscow research group), saw the infinite stretch and squeeze as a warning that Oppenheimer and Snyder’s idealized model of an imploding star could not be trusted. Recall that Oppenheimer and Snyder required, as a foundation for their calculations, that the star be precisely spherical and nonspinning and have uniform density, zero pressure, no shock waves, no ejected matter, and no outpouring radiation (Figure 13.2). These extreme idealizations were responsible for the singularity, Khalatnikov and Lifshitz argued. Every real star has tiny, random deformations (tiny, random nonuniformities in its shape, velocity, density, and pressure), and as the star implodes, they claimed, these deformations will grow large and halt the implosion before a singularity can form . Similarly, Khalatnikov and Lifshitz asserted, random deformations will halt the big crunch implosion of our entire Universe eons hence, and thereby save the Universe from destruction in a singularity.
Khalatnikov and Lifshitz came to these views in 1961 by asking themselves whether, according to Einstein’s general relativistic laws, singularities are stable against small perturbations . In other words, they posed the same question for singularities as we met in Chapter 7 for black holes: If, in solving Einstein’s field equation, we alter, in small but random ways, the shape of the imploding star or Universe and the velocity and density and pressure of its material, and if we insert into the material tiny but random amounts of gravitational radiation, how will these changes (these perturbations) affect the implosion’s predicted endpoint?
For the black hole’s horizon, as we saw in Chapter 7 , the perturbations make no difference. The perturbed, imploding star still forms a horizon, and although the horizon is deformed at first, all its deformations quickly get radiated away, leaving behind a completely “hairless” black hole. In other words, the horizon is stable against small perturbations.
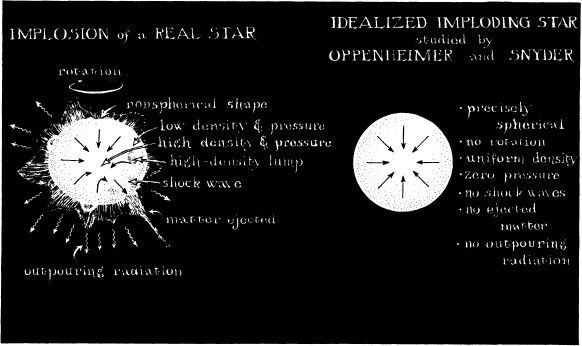
13.2 (Same as Figure 6.3.) Left: Physical phenomena in a realistic, imploding star. Right: The idealizations which Oppenheimer and Snyder made in order to compute stellar implosion. For a detailed discussion see Chapter 6 .
Not so for the singularity at the hole’s center or in the Universe’s final crunch, Khalatnikov and Lifshitz concluded. Their calculations seemed to show that tiny, random perturbations will grow large when the imploding matter attempts to create a singularity; they will grow so large, in fact, that they will prevent the singularity from forming. Presumably (though the calculations could not say for sure), the perturbations will halt the implosion and transform it into an explosion.
How could perturbations possibly reverse the implosion? The physical mechanism was not at all clear in the Khalatnikov–Lifshitz calculations. However, other calculations using Newton’s laws of gravity, which are far easier than calculations using Einstein’s laws, give hints. For example (see Figure 13.3), if gravity were weak enough inside an imploding star for Newton’s laws to be accurate, and if the star’s pressure were too small to be important, then small perturbations would cause different atoms to implode toward slightly different points near the star’s center. Most of the imploding atoms would miss the center by some small amount and would swing around the center and fly back out, thereby converting the implosion into an explosion. It seemed conceivable that, even though Newton’s laws of gravity fail inside a black hole, some mechanism analogous to this might convert the implosion into an explosion.
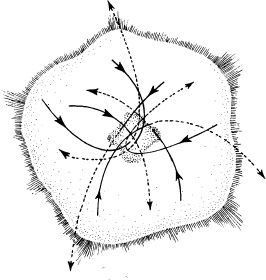
13.3 One mechanism for converting a star’s implosion into an explosion, when gravity is weak enough that Newton’s laws are accurate, and when internal pressure is weak enough to be unimportant. If the imploding star is slightly deformed (“perturbed”), its atoms implode toward slightly different points, swing around each other, and then fly back out.
I joined John Wheeler’s research group as a graduate student in 1962, shortly after Khalatnikov and Lifshitz had published their calculation, and shortly after Lifshitz together with Landau had enshrined the calculation and its “no singularity” conclusion in a famous textbook, The Classical Theory of Fields . I recall vividly Wheeler encouraging his research group to study the calculation. If it is right, its consequences are profound, he told us. Unfortunately, the calculation was extremely long and complicated, and the published details were too sketchy to permit us to check them-and Khalatnikov and Lifshitz were confined within the Soviet Union’s iron curtain, so we could not sit down with them and discuss the details.
Nevertheless, we began to contemplate the possibility that the imploding Universe, upon reaching some very small size, might “bounce” and reexplode in a new “big bang,” and similarly that an imploding star, after sinking inside its horizon, might bounce and reexplode.
But where could the star go if it reexplodes? It surely could not explode back out through the hole’s horizon. Einstein’s laws of gravity forbid anything (except virtual particles) to fly out of the horizon. There was another possibility, however: The star might manage to explode into some other region of our Universe, or even into another universe.
Figure 13.4 depicts such an implosion and reexplosion using a sequence of embedding diagrams. (Embedding diagrams, which are quite different from spacetime diagrams, were introduced in Figures 3.2 and 3.3.)
Each diagram in Figure 13.4 depicts our Universe’s curved space, and the curved space of another universe, as two-dimensional surfaces embedded in a higher-dimensional hyperspace . [Recall that hyperspace is a figment of the physicists’ imagination: We, as humans, are confined always to live in the space of our own Universe (or, if we can get there, the space of the other universe); we can never get out of those spaces into the surrounding higher-dimensional hyperspace, nor can we ever receive signals or information from hyperspace. The hyper-space serves only as an aid in visualizing the curvature of space around the imploding star and its black hole, and in visualizing the manner in which the star can implode in our Universe and then reexplode into another universe.]
In Figure 13.4, the two universes are like separate islands in an ocean and the hyperspace is like the ocean’s water. Just as there is no land connection between the islands, so there is no space connection between the universes.
The sequence of diagrams in Figure 13.4 depicts the star’s evolution. The star, in our Universe, is beginning to implode in diagram (a). In (b) the star has formed a black-hole horizon around itself and is continuing to implode. In (c) and (d) the star’s highly compressed matter curves space up tightly around the star, forming a little, closed universe that resembles the surface of a balloon; and this new, little universe pinches off from our Universe and moves, alone, out into hyperspace. (This is somewhat analogous to natives on one of the islands building a little boat and setting sail across the ocean.) In (d) and (e) the little universe, with the star inside, moves through hyperspace from our big Universe to the other big universe (like the boat sailing from one island to another). In (f) the little universe attaches itself to the other large universe (like the boat landing at the other island), and continues to expand, disgorging the star. In (g) and (h) the star explodes into the other universe.
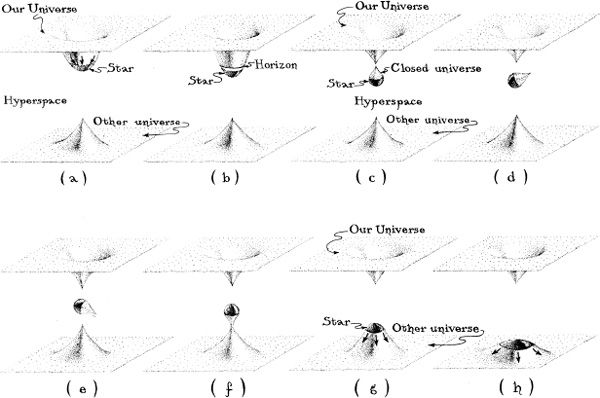
13.4 Embedding diagrams depicting a conceivable (though, as it turns out later in this chapter, a very unlikely ) fate of the star that implodes to form a black hole. The eight diagrams, (a) through (h), are a sequence of snapshots showing the evolution of the star and the geometry of space. The star implodes in our Universe (a), and forms a black-hole horizon around itself (b). Then deep inside the hole the region of space containing the star pinches off from our Universe and forms a small, closed universe with no connection to anything else (c). That closed universe then moves through hyperspace (d, e) and attaches itself to another large universe (I); and the star then explodes outward into that other universe (g, h).
I am uncomfortably aware that this scenario sounds like pure science fiction. However, just as black holes were a natural outgrowth of Schwarzschild’s solution to the Einstein field equation (Chapter 3 ), so also this scenario is a natural outgrowth of another solution to the Einstein equation, a solution found in 1916–18 by Hans Reissner and Gunnar Nordström but not fully understood by them. In 1960 two of Wheeler’s students, Dieter Brill and John Graves, deciphered the physical meaning of the Reissner–Nordström solution, and it soon became obvious that, with modest changes, the Reissner–Nordström solution would describe the imploding/exploding star of Figure 13.4. This star would differ from that of Oppenheimer and Snyder in just one fundamental way: It would contain within itself enough electric charge to produce a strong electric field when it gets highly compacted, and that electric field seemed in some way to be responsible for the star’s reexplosion into another universe.
L et us take stock of where things stood in 1964, in the quest for Wheeler’s holy grail—the quest to understand the ultimate fate of a star that implodes to form a black hole:
1. We knew one solution of Einstein’s equation (the Oppenheimer–Snyder solution) which predicts that, if the star has a highly idealized form, including a perfectly spherical shape, then it will create a singularity with infinite tidal gravity at the hole’s center—a singularity that captures, destroys, and swallows everything that falls into the hole.
2. We knew another solution of Einstein’s equation (an extension of the Reissner–Nordström solution) which predicts that, if the star has a somewhat different highly idealized form, including a spherical shape and electric charge, then deep inside the black hole the star will pinch off from our Universe, attach itself to another universe (or to a distant region of our own Universe), and there reexplode.
3. It was far from clear which, if either, of these solutions was “stable against small, random perturbations” and thus was a candidate for occurring in the real Universe.
4. Khalatnikov and Lifshitz had claimed to prove, however, that singularities are always unstable against small perturbations and thus never occur, and therefore the Oppenheimer–Snyder singularity could never occur in our real Universe.
5. In Princeton, at least, there was some skepticism about the Khalatnikov–Lifshitz claim. This skepticism may have been driven in part by Wheeler’s desire for singularities, since they would be a “marrying” place for general relativity and quantum mechanics.
Nineteen sixty-four was a watershed year. It was the year that Roger Penrose revolutionized the mathematical tools that we use to analyze the properties of spacetime. His revolution was so important, and had such great impact on the quest for Wheeler’s holy grail, that I shall digress for a few pages to describe his revolution and describe Penrose himself.
Penrose’s Revolution
R oger Penrose grew up in a British medical family; his mother was a physician, his father was an eminent professor of human genetics at University College in London, and his parents wanted at least one of their four children to follow in their footsteps with a medical career. Roger’s older brother Oliver was a dead loss; from an early age he was intent on a career in physics (and in fact would go on to become one of the world’s leading researchers in statistical physics—the study of the behaviors of huge numbers of interacting atoms). Roger’s younger brother Jonathon was also a dead loss; all he wanted to do was play chess (and in fact he would go on to become the British chess champion for seven years running). Roger’s little sister Shirley was much too young, when Roger was choosing a career, to show inclinations in any direction (though she ultimately would delight her parents by becoming a physician). That left Roger as his parents’ greatest hope.
At age sixteen Roger, like all the others in his class, was interviewed by the school’s headmaster. It was time to decide the topics for his last two years of pre-college study. “I’d like to do mathematics, chemistry, and biology,” he told the headmaster. “No. Impossible. You cannot combine biology with mathematics. It must be one or the other,” the headmaster proclaimed. Mathematics was more precious to Roger than biology. “All right, I’ll do mathematics, chemistry, and physics,” he said. When Roger got home that evening his parents were furious. They accused Roger of keeping bad company. Biology was essential to a medical career; how could he give it up?
Two years later came the decision of what to study in college. “I proposed to go to University College, London, and study for a mathematics degree,” Roger recalls. “My father didn’t approve at all. Mathematics might be all right for people who couldn’t do anything else, but it wasn’t the right thing to make a real career of.” Roger was insistent, so his father arranged for one of the College’s mathematicians to give him a special test. The mathematician invited Roger to take all day on the test, and warned him that he probably would be able to solve only one or two of the problems. When Roger solved all twelve problems correctly in a few hours, his father capitulated. Roger could study mathematics.
Roger initially had no intention of applying his mathematics to physics. It was pure math that interested him. But he got seduced.
The seduction began in 1952, when Roger as a fourth-year university student in London listened to a series of radio talks on cosmology by Fred Hoyle. The talks were fascinating, stimulating—and a bit confusing. A few of the things Hoyle said didn’t quite make sense. One day Roger took the train up to Cambridge to visit his brother Oliver, who was studying physics there. At the end of the day, over dinner at the Kingswood restaurant, Roger discovered that Dennis Sciama, Oliver’s officemate, was studying the Bondi–Gold–Hoyle steady-state theory of the Universe. How wonderful! Maybe Sciama could resolve Roger’s confusion. “Hoyle says that according to the steady-state theory the expansion of the Universe will drive a distant galaxy out of sight; the galaxy will move out of the observable part of our Universe. But I don’t see how this can be so.” Roger pulled out a pen and began drawing a spacetime diagram on a napkin. “This diagram makes me, think that the galaxy will become dimmer and dimmer, redder and redder, but will never quite disappear. What am I doing wrong?”
Sciama was taken aback. Never had he seen such power in a space time diagram. Penrose was right; Hoyle had to be wrong. More important, Oliver’s little brother was phenomenal.
Thereupon Dennis Sciama began with Roger Penrose the pattern he would continue with his own students in the 1960s (Stephen Hawking, George Ellis, Brandon Carter, Martin Rees, and others; see Chapter 7 ). He pulled Penrose into long discussions, sessions of many hours’ length, about the exciting things happening in physics. Sciama knew everything that was going on; he infused Penrose with his enthusiasm, with the excitement of it all. Soon Penrose was hooked. He would complete his Ph.D. in mathematics, but the quest to understand the Universe henceforth would drive him forward. He would spend the coming decades with one foot firmly planted in mathematics, the other in physics.

Roger Penrose, ca. 1964. [Photo by Godfrey Argent for the National Portrait Gallery of Britain and the Royal Society of London; courtesy Godfrey Argent.]
N ew ideas often arrive at the oddest moments, at moments when one is least expecting them. I suppose this is because they come from one’s subconscious mind, and the subconscious performs most effectively when the conscious part of the mind is not in high gear. A good example was Stephen Hawking’s 1970 discovery, as he was getting ready for bed, that the areas of black-hole horizons must always increase (Chapter 12 ). Another example is a discovery by Roger Penrose that changed our understanding of what is inside a black hole.
One day in the late autumn of 1964, Penrose, by then a professor at Birkbeck College in London, was walking toward his office with a friend, Ivor Robinson. For the past year, ever since quasars were discovered and astronomers began speculating that they are powered by stellar implosion (Chapter 9 ), Penrose had been trying to figure out whether singularities are created by realistic, randomly deformed, imploding stars. As he walked and talked with Robinson, his subconscious was mulling over the pieces of this puzzle—pieces with which his conscious mind had struggled for many many hours.
As Penrose recalls it, “My conversation with Robinson stopped momentarily as we crossed a side road, and resumed again at the other side. Evidently, during those few moments an idea occurred to me, but then the ensuing conversation blotted it from my mind! Later in the day, after Robinson had left, I returned to my office. I remember having an odd feeling of elation that I could not account for. I began going through in my mind all the various things that had happened to me during the day, in an attempt to find what it was that had caused this elation. After eliminating numerous inadequate possibilities, I finally brought to mind the thought that I had had while crossing the street.”
The thought was beautiful, unlike anything ever seen before in relativity physics. Carefully over the next few weeks Penrose manipulated it, looking at it from this direction and then from that, working through the details, making it as concrete and mathematically precise as he could. With all details in hand, he wrote a short article for publication in the journal Physical Review Letters , describing the issue of singularities in stellar implosion, and then proving a mathematical theorem.
Penrose’s theorem said roughly this: Suppose that a star—any kind of star whatsoever—implodes so far that its gravity becomes strong enough to form an apparent horizon , that is, strong enough to pull outgoing light rays back inward (Box 12.1). After this happens, nothing can prevent the gravity from growing so strong that it creates a singularity. Consequently (since black holes always have apparent horizons), every black hole must have a singularity inside itself.
The most amazing thing about this singularity theorem was its sweeping power. It dealt not solely with idealized imploding stars that have special, idealized properties (such as being precisely spherical or having no pressure); and it dealt not solely with stars whose initial random deformations are tiny. Instead, it dealt with every imploding star imaginable, and thus, undoubtedly, with the real imploding stars that inhabit our real Universe.
Penrose’s singularity theorem acquired its amazing power from a new mathematical tool that he used in its proof, a tool that no physicist had ever before used in calculations about curved spacetime, that is, in general relativistic calculations: topology.
Topology is a branch of mathematics that deals with the qualitative ways in which things are connected to each other or to themselves. For example, a coffee cup and a doughnut “have the same topology” because (if they are both made from putty) we can smoothly and continuously deform one into the other without tearing it, that is, without changing any connections (Figure 13.5a). By contrast, a sphere has a different topology from a doughnut; to deform a sphere into a doughnut, we must tear a hole in it, thereby changing how it is connected to itself (Figure 13.5b).
Topology cares only about connections, and not about shapes or sizes or curvatures. For example, the doughnut and the coffee cup have very different shapes and curvatures, but they have the same topology.
We physicists, before Penrose’s singularity theorem, ignored topology because we were fixated on the fact that spacetime curvature is the central concept of general relativity, and topology cannot tell us anything about curvature. (Indeed, because Penrose’s theorem was based so strongly on topology, it told us nothing about the singularity’s curvature, that is, nothing about the details of its tidal gravity. The theorem simply told us that somewhere inside the black hole, spacetime comes to an end, and anything that reaches that end gets destroyed. How it gets destroyed was the province of curvature; that it gets destroyed-that there is an end to spacetime—was the province of topology.)
If we physicists, before Penrose, had only looked beyond the issue of curvature, we would have realized that relativity does deal with questions of topology, questions such as “Does spacetime come to an end (does it have an edge beyond which spacetime ceases to exist)?” (Figure 13.5c) and “Which regions of spacetime can send signals to each other, and which cannot?” (Figure 13.5d). The first of these topological questions is central to singularities; the second is central to the formation and existence of black holes and also to cosmology (to the large-scale structure and evolution of the Universe).
These topological issues are so important, and the mathematical tools of topology are so powerful in dealing with them, that by introducing us to topology, Penrose triggered a revolution in our research.
Taking off from Penrose’s seminal ideas, during the middle and late 1960s Penrose, Hawking, Robert Geroch, George Ellis, and other physicists created a powerful set of combined topological and geometrical tools for general relativity calculations, tools that are now called global methods. Using these methods, Hawking and Penrose in 1970 proved—without any idealizing assumptions-that our Universe must have had a spacetime singularity at the beginning of its big bang expansion, and if it one day recollapses, it must produce a singularity in its big crunch. And using these global methods, Hawking in 1970 invented the concept of a black hole’s absolute horizon and proved that the surface areas of absolute horizons always increase (Chapter 12 ).
Let us return, now, to 1965. The stage was set for a momentous confrontation. Isaac Khalatnikov and Evgeny Lifshitz in Moscow had proved (or so they thought) that when a real star, with random internal deformations, implodes to form a black hole it cannot create a singularity at the hole’s center, while Roger Penrose in England had proved that every black hole must have a singularity at its center.
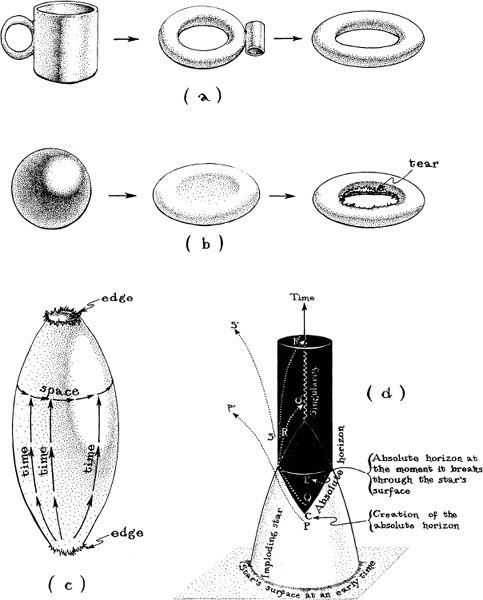
13.5 All of the following issues deal with the nature of the connections between points; that is, they are topological issues. (a) Acoffee cup (left) and a doughnut (right) can be deformed into each other smoothly and continuously without tearing, in other words, without changing the qualitative nature of any of the connections between points. They thus have the same topology. (b) To deform a sphere (left) into a doughnut (right), one must tear a hole in it. (c) The spacetime shown here has two sharp edges [analogous to the tear in (b)]: one edge at which time begins (analogous to the big bang beginning of our Universe), and one at which time ends (analogous to the big crunch). One can also conceive of a universe that has existed for all time and will always continue to exist; such a universe’s spacetime would have no edges. (d) The blackened region of spacetime is the interior of a black hole; the white region is the exterior (see Box 12.1). Points in the interior cannot send any signals to points in the exterior.
T he lecture hall seated 250 and was filled to overflowing as Isaac Khalatnikov rose to speak. It was a warm summer day in 1965, and the world’s leading relativity researchers had gathered in London for the Third International Conference on General Relativity and Gravitation. This was the first opportunity, at such a worldwide gathering, for Isaac Khalatnikov and Evgeny Lifshitz to present the details of their proof that black holes do not contain singularities.
Permission to travel beyond the iron curtain was granted and with-drawn with relative capriciousness in the Soviet Union during the decades between Stalin’s death and the Gorbachev era. Lifshitz, though Jewish, had traveled rather freely in the late 1950s, but he was now on a travel blacklist and would remain so until 1976. Khalatnikov had two strikes against him; he was Jewish, and he had never yet traveled abroad. (Permission for one’s first trip was exceedingly difficult to win.) However, after a vigorous struggle, including a telephone call in his behalf from the vice-president of the Academy of Sciences, Nikolai Nikolaievich Semenov, to the Central Committee of the Communist party, Khalatnikov had finally won permission to come to London.
As he spoke in the packed London lecture hall, dragging a microphone with him, Khalatnikov wrote equations all over the blackboard, which extended the entire 50-foot width of the room. His were not topological methods; they were the standard, equation-intensive methods that physicists had used for decades when analyzing spacetime curvature. Khalatnikov demonstrated mathematically that random perturbations must grow as a star implodes. This meant, he asserted, that if the implosion is to form a singularity, it must be one with completely random deformations in its spacetime curvature. He then described how he and Lifshitz had searched, among all types of singularities permitted by the laws of general relativity, for one with completely random curvature deformations. He exhibited, mathematically, one type of singularity after another; he cataloged the types of singularities almost ad nauseum . Among them, none had completely random deformations. Therefore, he concluded—bringing his fortyminute lecture to a close—an imploding star with random perturbations cannot produce a singularity. The perturbations must save the star from destruction.
As the applause ended, Charles Misner, one of Wheeler’s most brilliant former students, leaped up and objected strenuously. Excitedly, vigorously, and in rapid-fire English, Misner described the theorem that Penrose had proved a few months earlier. If Penrose’s theorem was right, then Khalatnikov and Lifshitz must be wrong.
The Soviet delegation was confused and incensed. Misner’s English was too fast to follow, and since Penrose’s theorem relied on topological arguments that were alien to relativity experts, the Soviets regarded it as suspect. By contrast, the Khalatnikov–Lifshitz analysis was based on tried-and-true methods. Penrose, they asserted, was probably wrong.
D uring the next few years, relativity experts in East and West plumbed the depths of Penrose’s analysis, and of the Khalatnikov–Lifshitz analysis. At first both analyses looked suspect; both had dangerous, potential flaws. Gradually, however, as the experts began to master and extend Penrose’s topological techniques, they became convinced that Penrose was right.
In September 1969, while I was a visiting member of Zel’dovich’s research team in Moscow, Evgeny Lifshitz came to me with a manuscript that he and Khalatnikov had just written. “Please, Kip, take this manuscript back to America for me and submit it to Physical Review Letters ”, he requested. He explained that any manuscript written in the U.S.S.R., regardless of its content, was automatically classified secret until declassified, and declassification would take three months. The ludicrous Soviet system permitted me or any other foreign visitor to read the manuscript while in Moscow, but the manuscript should not itself leave the country until passed by the censors. This manuscript was too precious, too urgent for such a ridiculous delay. It contained, Lifshitz explained to me, their capitulation, their confession of error: Penrose was right; they were wrong. In 1961 they had been unable to find, among the solutions to Einstein’s field equation, any singularity with completely random deformations; but now, spurred by Penrose’s theorem, they and a graduate student, Vladimir Belinsky, had managed to find one. This new singularity, they thought, must be the one that terminates the implosion of randomly deformed stars and that might someday destroy our Universe at the end of the big crunch. [And, indeed, in 1993 I think they probably were right. To this 1993 viewpoint, and to the nature of their new BKL (“Belinsky–Khalatnikov–Lifshitz”) singularity, I shall return near the end of this chapter.]
A dinner party in the apartment of Isaac Khalatnikov in Moscow, June 1971. Clockwise from left: Kip Thorne, John Wheeler, Evgeny Lifshitz, Isaac Khalatnikov, Khalatnikov’s wife Valentina Nikolaievna, Vladimir Belinsky, and Khalatnikov’s daughter Eleanora. [Courtesy Charles W. Misner.]
For a theoretical physicist it is more than embarrassing to admit a major error in a published result. It is ego shattering. I should know. In 1966 I miscalculated the pulsations of white-dwarf stars, and two years later my wrong calculations briefly misled astronomers into thinking that the newly discovered pulsars might be pulsating white dwarfs. My error, when found, was significant enough to figure in an editorial in the British journal Nature . It was a bitter pill to swallow.
Though errors like this can be shattering for an American or European physicist, in the Soviet Union they were far worse. One’s position in the pecking order of scientists was especially important in the Soviet Union; it determined such things as possibilities for travel abroad and election to the Academy of Sciences, which in turn brought privileges such as a near doubling of one’s salary and a chauffeured limousine at one’s beck and call. Thus it was that the temptation to try to hide or downplay mistakes, when mistakes occur, was greater for Soviet scientists than for Westerners. And thus it was that Lifshitz’s plea for help was impressive. He wanted no delay in disseminating the truth, and his manuscript was forthright: It confessed the error and announced that future editions of The Classical Theory of Fields (the Landau–Lifshitz textbook on general relativity) would be modified to remove the claim that implosion does not produce singularities.
I carried the manuscript to America, hidden among my personal papers, and it was published. The Soviet authorities never noticed.
W hy was it a British physicist (Penrose) and not an American or French or Soviet physicist who introduced topological methods into relativity research? And why was it that throughout the 1960s, topological methods were pursued with vigor and success by other British relativity physicists, but took hold much more slowly in America, France, the U.S.S.R., and elsewhere?
The reason, I suspect, was the undergraduate training of British theoretical physicists. They typically major in mathematics as undergraduates, then do Ph.D. research in departments of applied mathematics or departments of applied mathematics and theoretical physics. In America, by contrast, aspiring theoretical physicists typically major in physics as undergraduates, and then do Ph.D. research in physics departments. Thus, young British theoretical physicists are well versed in esoteric branches of mathematics which have not yet seen much physics application, but they may have a weak background in “gutsy” physics topics such as the behaviors of molecules, atoms, and atomic nuclei. By contrast, young American theoretical physicists know little mathematics beyond what their physics professors have taught them, but are deeply versed in the lore of molecules, atoms, and nuclei.
To a great extent, we Americans have dominated theoretical physics since World War II, and we have foisted on the world’s physics community our scandalously low mathematical standards. Most of us use the mathematics of fifty years ago and are incapable of communicating with modern mathematicians. With our poor mathematical training, it was difficult for us Americans to absorb and start using the topological methods when Penrose introduced them.
French theoretical physicists, even more than the British, are well trained in mathematics. However, during the 1960s and 1970s French relativity theorists were so wrapped up in mathematical rigor (that is, perfection), and so deemphasized physical intuition, that they contributed little to our understanding of imploding stars and black holes. Their quest for rigor slowed them down to the point that, although they knew well the mathematics of topology, they could not compete with the British. They didn’t even try; their attention was riveted elsewhere.
Lev Davidovich Landau, who was largely responsible for the strength of Soviet theoretical physics in the 1930s through 1960s, was also a source of Soviet resistance to topology: Landau had transfused theoretical physics from Western Europe to the U.S.S.R. in the 1930s (Chapter 5 ). As one tool in that transfusion, he had created a set of examinations on theoretical physics, called the “Theoretical Minimum”, which he required be passed as an entree into his own research group. Anyone, regardless of educational background, could walk in off the street and take these examinations, but few could pass them. In the twenty-nine years of the Theoretical Minimum (1933–62) only forty-three passed, but a remarkable portion of those forty-three went on to make great physics discoveries.

Evgeny Michailovich Lifshitz (left) and Lev Davidovich Landau (right) in Landau’s room in his flat at the Institute for Physical Problems, No. 2 Vorobyevskoye Shosse, Moscow, in 1954. [Courtesy Lifshitz’s wife, Zinaida Ivanovna Lifshitz.]
Landau’s Theoretical Minimum had included problems from all the branches of mathematics that Landau deemed important for theoretical physics. Topology was not among them. Calculus, complex variables, the qualitative theory of differential equations, group theory, and differential geometry were all covered; they would all be needed in a physicist’s career. But topology would not be needed. Landau had nothing against topology; he just ignored it; it was irrelevant—and his view of its irrelevance became near gospel among most Soviet theoretical physicists in the 1940s through the 1960s.
This view was transmitted to theoretical physicists around the world by the set of textbooks, called Course of Theoretical Physics , that Landau and Lifshitz wrote. These became, worldwide, the most influential set of physics texts of the twentieth century, and like Landau’s Theoretical Minimum examinations, they ignored topology.
Curiously, topological techniques were introduced into relativity research in an abortive way, long before Penrose’s theorem, by two Soviet mathematicians in Leningrad: Aleksander Danilovich Aleksandrov and Revol’t Ivanovich Pimenov. In 1950–59, Aleksandrov used topology to probe the “causal structure” of spacetime, that is, to study the relationships between regions of spacetime that can communicate with each other and those that cannot. This was just the type of topological analysis that would ultimately pay rich dividends in the theory of black holes. Aleksandrov built up a rather powerful and beautiful topological formalism, and in the mid-1950s that formalism was picked up and pushed further by Pimenov, a young colleague of Aleksandrov’s.
But in the end this research led nowhere. Aleksandrov and Pimenov had little contact with physicists who specialize in gravitation. Such physicists would have known what kinds of calculations were useful and what were not. They might have told Aleksandrov and Pimenov that the big bang singularity or gravitational implosion of stars deserved probing with their formalism. But no such advice was to be had in Leningrad; the key physicists worked 600 kilometers southeast of Leningrad, in Moscow, and were ignorant of topology and topologists. The Aleksandrov–Pimenov formalism flowered, and then went dormant.
Its dormancy was forced by the fates of Aleksandrov and Pimenov: Aleksandrov became the rector (president) of Leningrad University, and had inadequate time for further research. Pimenov was arrested in 1957 for founding “an anti-Soviet group,” was imprisoned for six years, and then after seven years of freedom was rearrested and sent into five years’ exile in the Komi Republic, 1200 kilometers east of Leningrad.
I have never met Aleksandrov or Pimenov, but tales of Pimenov were still rippling through Leningrad’s community of scientists when I visited there in 1971, a year after Pimenov’s second arrest. Rumor had it that Pimenov viewed the Soviet government as morally corrupt, and, like many young people in America during the Vietnam War, he felt that, if he cooperated with the government, the government’s corruption would rub off on him. The only way to feel morally clean was through civil disobedience. In America, civil disobedience meant refusing to register for the draft. For Pimenov, civil disobedience meant samizdat . Samizdat was the “self-publication” of forbidden manuscripts. Pimenov, it was rumored, would receive from friends a manuscript which had been forbidden for publication in the Soviet Union, he would type out a half-dozen copies using carbon paper, and he would then pass those copies on to other friends, who would repeat the process. Pimenov got caught, was convicted, and was sentenced to five years’ exile in the Komi Republic, where he worked as a tree-feller and an electrician in a sawmill until the Komi Academy of Sciences took advantage of his exile and made him the chair of their mathematics department.
Finally able to do mathematics again, Pimenov continued his topological studies of spacetime. By then topology had taken firm root as a key tool for physicists’ gravitation research, but Pimenov remained isolated from the leading physicists of his country. He never had the impact that, under other circumstances, he might have.
Roger Penrose, by contrast with Aleksandrov and Pimenov, lives with one foot firmly planted in the mathematics community and the other firmly planted in physics, and this has been a major source of his success.
Best Guesses
O ne might have thought that Penrose’s singularity theorem would settle once and for all the question of what is inside a black hole. Not so. Instead it opened up a new set of questions—questions with which physicists have struggled, with only modest success, since the mid-1960s. Those questions, and our best 1993 answers (our “best guesses” is a better way to say it), are:
1. Does everything that enters the hole necessarily get swallowed by the singularity? We think so, but we’re not sure.
2. Is there any route from inside the hole to another universe, or to another part of our own Universe? Very probably not, but we’re not absolutely sure.
3. What is the fate of things that fall into the singularity? We think that things that fall in when the hole is quite young get torn apart by tidal gravity in a violent, chaotic way, before quantum gravity becomes important. However, things that fall into an old hole might survive unscathed until they come face-to-face with the laws of quantum gravity.
In the remainder of this chapter I shall explain these answers in more detail.
R ecall that Oppenheimer and Snyder gave us a clear and unequivocal answer to our three questions: When the black hole is created by a highly idealized, spherical, imploding star, then (1) everything that enters the hole gets swallowed by the singularity; (2) nothing travels to another universe or another part of our Universe; (3) when nearing the singularity, everything experiences an infinitely growing radial stretch and transverse squeeze (Figure 13.1 above), and thereby gets destroyed. This answer was pedagogically useful; it helped motivate calculations that brought deeper understanding. However, the deeper understanding (due to Khalatnikov and Lifshitz) showed that the Oppenheimer–Snyder answer is irrelevant to the real Universe in which we live, because the random deformations that occur in all real stars will completely change the hole’s interior. The Oppenheimer–Snyder interior is “unstable against small perturbations.”
The Reissner-Nordstrom type of solution to the Einstein field equation also gave a clear and unequivocal answer: When the black hole is created by a particular, highly idealized, spherical, electrically charged star, then the imploding star and other things that fall into the hole can travel, via a “little closed universe,” from the hole’s interior to another large universe (Figure 13.4).
This answer was also pedagogically useful (and has provided grist for the mills of many a science fiction writer). However, like the Oppenheimer–Snyder prediction, it has nothing to do with the real Universe in which we live because it is unstable against small perturbations. More specifically, in our real Universe, the black hole is continually bombarded by tiny electromagnetic vacuum fluctuations and by tiny amounts of radiation. As these fluctuations and radiation fall into the hole, the hole’s gravity accelerates them to enormous energy, and they then explosively hit and destroy the little closed universe, just before the little universe begins its trip. This was conjectured by Penrose in 1968, and has since been verified in many different calculations, carried out by many different physicists.
Belinsky, Khalatnikov, and Lifshitz have given us yet another answer to our questions, and this one, being totally stable against small perturbations, is probably the “right” answer, the answer that applies to the real black holes that inhabit our Universe: The star that forms the hole and everything that falls into the hole when the hole is young get torn apart by the tidal gravity of a BKL singularity . (This is the kind of singularity that Belinsky, Khalatnikov, and Lifshitz discovered, as a solution of Einstein’s equation, after Penrose convinced them that singularities must inhabit black holes.)
The tidal gravity of a BKL singularity is radically different from that of the Oppenheimer–Snyder singularity. The Oppenheimer–Snyder singularity stretches and squeezes an infalling astronaut (or anything else) in a steady but mounting way; the stretch is always radial, the squeeze is always transverse, and the strengths of stretch and squeeze grow steadily and smoothly (Figure 13.1). The BKL singularity, by contrast, is somewhat like the taffy-pulling machines that one sometimes sees in candy stores or at carnivals. It stretches and squeezes first in this direction, then that, then another, then another, and yet another. The stretch and squeeze oscillate with time in a random and chaotic way (as measured by the infalling astronaut), but on average they get stronger and stronger, and their oscillations get faster and faster as the astronaut gets closer and closer to the singularity. Charles Misner (who discovered this type of chaotically oscillating singularity independently of Belinsky, Khalatnikov, and Lifshitz) has called this a mixmaster oscillation because one can imagine it mixing up the astronaut’s body parts in the way that a mixmaster or eggbeater mixes up the yolk and white of an egg. Figure 13.6 depicts a specific example of how the tidal forces might oscillate, but the precise sequence of oscillations is chaotically unpredictable.
In Misner’s version of the mixmaster singularity, the oscillations were the same everywhere in space, at a particular moment of time (as measured, say, by the astronaut). Not so for the BKL singularity. Its oscillations are spatially chaotic as well as temporally chaotic, just as turbulent motions of the froth in a breaking ocean wave are chaotic in space as well as in time. For example, while the astronaut’s head is being alternately stretched and squeezed (“pummeled”) along the north/south direction, his right foot might be pummeled along the northeast/southwest direction, and his left foot along south-southeast/north-northwest; and the frequencies of oscillation of the pummeling might be quite different on his head, his left foot, and his right foot.
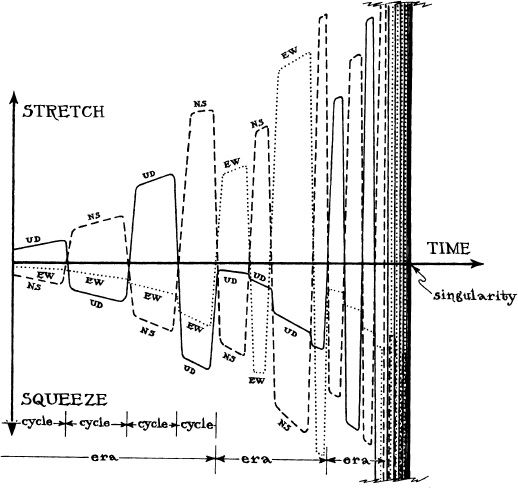
13.6 An example of how the tidal forces might oscillate with time in a BKL singularity. The tidal forces act in different manners along three different, perpendicular directions. These directions, for definiteness, are here called UD (for “up/down”), NS (for “north/south”), and EW (for “east/west”), and each of the three curves describes the behavior of the tidal force along one of these directions. Time is plotted horizontally. At any time when the UD curve is above the horizontal time axis, the tidal force is stretching along the UD direction, while at a time when the UD curve is below the axis, the un tidal force is squeezing. The higher the curve above the axis, the stronger the stretch; the lower the curve below the axis, the stronger the squeeze. Notice the following: (i) At any moment of time there is a squeeze along two directions and a stretch along one. (H) The tidal forces oscillate between stretch and squeeze; each oscillation is called a “cycle.” (iii) The cycles are collected into “eras.” During each era, one of the three directions is subjected to a fairly steady squeeze, while the other two oscillate between stretch and squeeze. (iv) When the era changes, there is a change of the steady direction. (v) As the singularity is approached, the oscillations become infinitely rapid and the tidal forces become infinitely strong. The details of the division of cycles into eras and the change of oscillation patterns at the beginning of each era are governed by what is sometimes called a “chaotic map.”
Einstein’s equation predicts that, as the astronaut reaches the singularity, the tidal forces grow infinitely strong, and their chaotic oscillations become infinitely rapid. The astronaut dies and the atoms from which his body is made become infinitely and chaotically distorted and mixed—and then, at the moment when everything becomes infinite (the tidal strengths, the oscillation frequencies, the distortions, and the mixing), spacetime ceases to exist.
T he laws of quantum mechanics object. They forbid the infinities. Very near the singularity, as best we understand it in 1993, the laws of quantum mechanics merge with Einstein’s general relativistic laws and completely change the “rules of the game.” The new rules are called quantum gravity.
The astronaut is already dead, his body parts are already thoroughly mixed, and the atoms of which he was made are already distorted beyond recognition when quantum gravity takes over. But nothing is infinite. The “game” goes on.
Just when does quantum gravity take over, and what does it do? As best we understand it in 1993 (and our understanding is rather poor), quantum gravity takes over when the oscillating tidal gravity (spacetime curvature) becomes so large that it completely deforms all objects in about 10 −43 second or less. 2 Quantum gravity then radically changes the character of spacetime: It ruptures the unification of space and time into spacetime. It unglues space and time from each other, and then destroys time as a concept and destroys the definiteness of space. Time ceases to exist; no longer can we say that “this thing happens before that one,” because without time, there is no concept of “before” or “after.” Space, the sole remaining remnant of what was once a unified spacetime, becomes a random, probabilistic froth, like soapsuds.
Before its rupture (that is, outside the singularity), spacetime is like a piece of wood impregnated with water. In this analogy, the wood represents space, the water represents time, and the two (wood and water; space and time) are tightly interwoven, unified. The singularity and the laws of quantum gravity that rule it are like a fire into which the water-impregnated wood is thrown. The fire boils the water out of the wood, leaving the wood alone and vulnerable; in the singularity, the laws of quantum gravity destroy time, leaving space alone and vulnerable. The fire then converts the wood into a froth of flakes and ashes; the laws of quantum gravity then convert space into a random, probabilistic froth.
This random, probabilistic froth is the thing of which the singularity is made, and the froth is governed by the laws of quantum gravity. In the froth, space does not have any definite shape (that is, any definite curvature, or even any definite topology). Instead, space has various probabilities for this, that, or another curvature and topology. For example, inside the singularity there might be a 0.1 percent probability for the curvature and topology of space to have the form shown in Figure 13.7a, and a 0.4 percent probability for the form in Figure 13.7b, and a 0.02 percent probability for the form in Figure 13.7c, and so on. This does not mean that space spends 0.1 percent of its time in the form (a), 0.4 percent of its time in the form (b), and 0.02 percent of its time in the form (c), because there is no such thing as time inside the singularity. And similarly, because there is no time, it is totally meaningless to ask whether space assumes the form (b) “before” or “after” it assumes the form (c). The only meaningful question one can ask of the singularity is, “What are the probabilities that the space of which you are made has the forms (a), (b), and (c)?” And the answers will be simply 0.1, 0.4, and 0.02 percent.
Because all conceivable curvatures and topologies are permitted inside the singularity, no matter how wild, one says that the singularity is made from a probabilistic foam. John Wheeler, who first argued that this must be the nature of space when the laws of quantum gravity hold sway, has called it quantum/foam.
To recapitulate, at the center of a black hole, in the spacetime region where the oscillating BKL tidal forces reach their peak, there resides a singularity: a region in which time no longer exists, and space has given way to quantum foam.
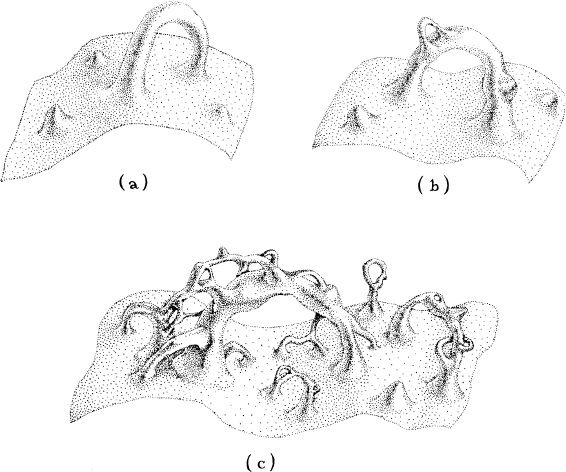
13.7 Embedding diagrams illustrating the quantum foam that is thought to reside in the singularity inside a black hole. The geometry and topology of space are not definite; instead, they are probabilistic. They might have, for example, a 0.1 percent probability for the form shown in (a), a 0.4 percent probability for (b), a 0.02 percent probability for (c), and so on.
One task of the laws of quantum gravity is to govern the probabilities for the various curvatures and topologies within a black hole’s singularity. Another, presumably, is to determine the probabilities for the singularity to give birth to “new universes,” that is, to give birth to new, classical (non-quantum) regions of spacetime, in the same sense as the big bang singularity gave birth to our Universe some 15 billion years ago.
How probable is it that a black hole’s sirlgularity will give birth to “new universes”? We don’t know. It might well never happen, or it might be quite common—or we might be on completely the wrong track in believing that singularities are made of quantum foam.
Clear answers might come in the next decade or two from research now being carried out by Stephen Hawking, James Hartle, and others, building on foundations laid by John Wheeler and Bryce DeWitt. 3
M ost everything in the Universe changes with age: Stars consume their fuel and die; the Earth gradually loses its atmosphere by evaporation into space and ultimately will become an airless, dead planet; and we humans grow wrinkled and wise.
The tidal forces deep inside a black hole, near its singularity, are no exception. They, too, must change with age, according to calculations done in 1991 by Werner Israel and Eric Poisson of the University of Alberta, and Amos Ori, a postdoc in my Caltech group (building on earlier work of Andrei Doroshkevich and Igor Novikov). When the hole is newborn, its interior tidal forces exhibit violent, chaotic, BKL-type oscillations (Figure 13.6 above). However, as the hole ages, the chaotic oscillations become tamer and gentler, and gradually disappear.
For example, an astronaut who falls into a 10-billion-solar-mass hole in the core of a quasar within the first few hours after the hole is born will be torn apart by wildly oscillating BKL tidal forces. However, a second astronaut, who waits until a day or two after the hole is born before plunging inside, will encounter much more gently oscillating tidal forces. The tidal stretch and squeeze are still large enough to kill the second astronaut, but being more gentle than the day before, the oscillating stretch and squeeze will allow the second astronaut to survive longer, and approach closer to the singularity before he dies, than did the first astronaut. A third astronaut, who waits until the hole is many years old before taking the plunge, will face an even gentler fate. The tidal forces surrounding the singularity have now become so tame and meek, according to Israel’s, Poisson’s, and Ori’s calculations, that the astronaut will hardly feel them at all. He will survive, almost unscathed, right up to the edge of the probabilistic quantum gravity singularity. Only at the singularity’s edge, just as he comes face-to-face with the laws of quantum gravity, will the astronaut be killed—and we cannot even be absolutely sure he gets killed then, since we do not really understand at all well the laws of quantum gravity and their consequences.
This aging of a black hole’s internal tidal forces is not inexorable. Whenever matter and radiation (or astronauts) fall into the hole, they will feed and energize the tidal forces, much like a hunk of meat thrown to a lion energizes him. The oscillatory stretch and squeeze near the singularity, having been fed, will grow stronger for a short while, and then will die out and become quiescent once again.
I n the late 1950s and early 1960s John Wheeler had a dream, a hope, that we humans might one day be able to probe into a singularity and there see quantum gravity at work—that we might probe not only with mathematics and computer simulations, but also with real, physical observations and experiments. Oppenheimer and Snyder dashed that hope (Chapter 6 ). The horizon that they discovered forming around an imploding star hides the singularity from external view. If we remain forever outside the horizon, there is no way that we can probe the singularity. And if we plunge through the horizon of a huge old hole, and survive to meet the quantum gravity singularity face-to-face, there is no way we can transmit a description of our meeting back to Earth. Our transmission cannot escape from the hole; the horizon hides it.
Though Wheeler has long since renounced his dream and now vigorously champions the view that it is impossible to probe singularities, it is not at all certain that he is correct. It is conceivable that some extremely nonspherical stellar implosions produce naked singularities , that is, singularities that are not surrounded by horizons and that therefore can be observed and probed from the external Universe, even from Earth.
In the late 1960s, Roger Penrose searched hard, mathematically, for an example of an implosion that creates a naked singularity. His search came up empty. Whenever, in his equations, an implosion created a singularity, it also created a horizon around the singularity. Penrose was not surprised. After all, if a naked singularity were to form, then it seems reasonable to expect that, just before the singularity forms, light can escape from its vicinity; and if light can escape, then (it would seem) so can the material that is imploding to create the singularity; and if the imploding material can escape, then presumably the material’s huge internal pressure will make it escape, thereby reversing the implosion and preventing the singularity from forming in the first place. So it seemed. However, neither Penrose’s mathematical manipulations nor anybody else’s were powerful enough to say for sure.
In 1969 Penrose, strongly convinced that naked singularities cannot form, but unable to prove it, proposed a conjecture, the conjecture of cosmic censorship: No imploding object can ever form a naked singularity; if a singularity is formed, it must be clothed in a horizon so that we in the external Universe cannot see it
Members of the physics “establishment”—physicists like John Wheeler, whose viewpoints are the most influential—have embraced cosmic censorship and espouse it as almost surely correct. Nevertheless, nearly a quarter century after Penrose proposed it, cosmic censorship remains unproved; and recent computer simulations of the implosion of highly nonspherical stars suggest that it might even be wrong. Some implosions, according to these simulations by Stuart Shapiro and Saul Teukolsky of Cornell University, might actually create naked singularities. Might. Not will; just might.
Stephen Hawking is the epitome of the establishment these days, and John Preskill (a colleague of mine at Caltech) and I enjoy tweaking the establishment a bit. Therefore, in 1991 Preskill and I made a bet with Hawking (Figure 13.8). We bet that cosmic censorship is wrong; naked singularities can form in our Universe. Hawking bet that cosmic censorship is right; naked singularities can never form.

13.8 Bet between Stephen Hawking, John Preskill, and me on the correctness of Penrose’s cosmic censorship conjecture.
Just four months after agreeing to the bet, Hawking himself discovered mathematical evidence (but not a firm proof ) that, when a black hole completes its evaporation (Chapter 12 ), it might not disappear entirely as he had previously expected, but instead it might leave behind a tiny naked singularity. Hawking announced this result to Preskill and me privately, a few days after he discovered it, at a dinner party at Preskill’s home. However, when Preskill and I then pressed him to concede our bet, he refused on grounds of a technicality. The wording of our bet was very clear, he insisted: The bet was restricted to naked singularities whose formation is governed by the laws of classical (that is, not quantum) physics, including the laws of general relativity. However, the evaporation of black holes is a quantum mechanical phenomenon and is governed not by the laws of classical general relativity, but rather by the laws of quantum fields in curved spacetime, so any naked singularity that might result from black-hole evaporation is outside the realm of our bet, Hawking insisted (correctly). Nevertheless, a naked singularity, however it forms, would surely be a blow to the establishment!
Though we enjoy our bets, the issues we argue are deeply serious. If naked singularities can exist, then only the ill-understood laws of quantum gravity can tell us how they behave, what they might do to spacetime in their vicinities, and whether their actions can have a large effect on the Universe in which we live, or only a small one. Because naked singularities, if they can exist, might strongly influence our Universe, we want very much to understand whether cosmic censorship is correct, and what the laws of quantum gravity predict for the behaviors of singularities. The struggle to find out will not be quick or easy.
1. In technical jargon, we say that the singularity is “spacelike.”
2.
10
−43
second is the
Planck–Wheeler time
. It is given (approximately) by the formula
![]() , where
G
=6.670 × 10
–8
dyne-centimeter
2
/gram
2
is Newton’s gravitation constant,
ħ
= 1.055 × 10
–27
erg-second is Planck’s quantum mechanical constant, and
c
= 2.998 × 10
10
centimeter/second is the speed of light. Note that the Planck-Wheeler time is equal to the square root of the Planck–Wheeler area (
Chapter 12
) divided by the speed of light.
, where
G
=6.670 × 10
–8
dyne-centimeter
2
/gram
2
is Newton’s gravitation constant,
ħ
= 1.055 × 10
–27
erg-second is Planck’s quantum mechanical constant, and
c
= 2.998 × 10
10
centimeter/second is the speed of light. Note that the Planck-Wheeler time is equal to the square root of the Planck–Wheeler area (
Chapter 12
) divided by the speed of light.
3. The above description is based on the Wheeler–DeWitt, Hawking–Hartle approach to formulating the laws of quantum gravity. Although theirs is but one of many approaches now being pursued, it is one to which I would give good odds of success.
14
![]()
in which the author seeks insight
into physical laws by asking:
can highly advanced civilizations
build wormholes through hyperspace
for rapid interstellar travel
and machines for traveling backward in time?
Wormholes and Exotic Material
I had just taught my last class of the 1984–85 academic year and was sinking into my office chair to let the adrenaline subside, when the telephone rang. It was Carl Sagan, the Cornell University astrophysicist and a personal friend from way back. “Sorry to bother you, Kip,” he said. “But I’m just finishing a novel about the human race’s first contact with an extraterrestrial civilization, and I’m worried. I want the science to be as accurate as possible, and I’m afraid I may have got some of the gravitational physics wrong. Would you look at it and give me advice?” Of course I would. It would be interesting, since Carl is a clever guy. It might even be fun. Besides, how could I turn down this kind of request from a friend?
The novel arrived a couple of weeks later, a three-and-a-half-inch-thick stack of double-spaced typescript.
I slipped the stack into an overnight bag and threw the bag into the back seat of Linda’s Bronco, when she picked me up for the long drive from Pasadena to Santa Cruz. Linda is my ex-wife; she, I, and our son Bret were on our way to see our daughter Kares graduate from college.
As Linda and Bret took turns driving, I read and thought. (Linda and Bret were accustomed to such introversion; they had lived with me for many years.) The novel was fun, but Carl, indeed, was in trouble. He had his heroine, Eleanor Arroway, plunge into a black hole near Earth, travel through hyperspace in the manner of Figure 13.4, and emerge an hour later near the star Vega, 26 light-years away. Carl, not being a relativity expert, was unfamiliar with the message of perturbation calculations 2 : It is impossible to travel through hyperspace from a black hole’s core to another part of our Universe. Any black hole is continually being bombarded by tiny electromagnetic vacuum fluctuations and by tiny amounts of radiation. As these fluctuations and radiation fall into the hole, they get accelerated by the hole’s gravity to enormous energy, and they then rain down explosively on any “little closed universe” or “tunnel” or other vehicle by which one might try to launch the trip through hyperspace. The calculations were unequivocal; any vehicle for hyperspace travel gets destroyed by the explosive “rain” before the trip can be launched. Carl’s novel had to be changed.
During the return drive from Santa Cruz, somewhere west of Fresno on Interstate 5, a glimmer of an idea came to me. Maybe Carl could replace his black hole by a wormhole through hyperspace.
A wormhole is a hypothetical shortcut for travel between distant points in the Universe. The wormhole has two entrances called “mouths,” one (for example) near Earth, and the other (for example) in orbit around Vega, 26 light-years away. The mouths are connected to each other by a tunnel through hyperspace (the wormhole) that might be only a kilometer long. If we enter the near-Earth mouth, we find ourselves in the tunnel. By traveling just one kilometer down the tunnel we reach the other mouth and emerge near Vega, 26 light-years away as measured in the external Universe.
Figure 14.1 depicts such a wormhole in an embedding diagram. This diagram, as is usual for embedding diagrams, idealizes our Universe as having only two spatial dimensions rather than three (see Figures 3.2 and 3.3). In the diagram the space of our Universe is depicted as a two-dimensional sheet. Just as an ant crawling over a sheet of paper is oblivious to whether the paper is lying flat or is gently folded, so we in our Universe are oblivious to whether our Universe is lying flat in hyperspace or is gently folded, as in the diagram. However, the gentle fold is important; it permits the Earth and Vega to be near each other in hyperspace so they can be connected by the short wormhole. With the wormhole in place, we, like an ant or worm crawling over the embedding diagram’s surface, have two possible routes from Earth to Vega: the long, 26-light-year route through the external Universe, and the short, 1-kilometer route through the wormhole.
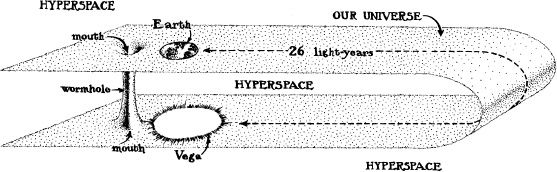
14.1 A1-kilometer-Iong wormhole through hyperspace linking the Earth to the neighborhood of Vega, 26 light-years away. (Not drawn to scale.)
What would the wormhole’s mouth look like, if it were on Earth, in front of us? In the diagram’s two-dimensional universe the wormhole’s mouth is drawn as a circle; therefore, in our three-dimensional Universe it would be the three-dimensional analogue of a circle; it would be a sphere. In fact, the mouth would look something like the spherical horizon of a nonrotating black hole, with one key exception: The horizon is a “one-way” surface; anything can go in, but nothing can come out. By contrast, the wormhole mouth is a “two-way” surface; we can cross it in both directions, inward into the wormhole, and back outward to the external Universe. Looking into the spherical mouth, we can see light from Vega; the light has entered the other mouth near Vega and has traveled through the wormhole, as though the wormhole were a light pipe or optical fiber, to the near-Earth mouth, where it now emerges and strikes us in the eyes.
Wormholes are not mere figments of a science fiction writer’s imagination. They were discovered by Ludwig Flamm mathematically, as a solution to Einstein’s field equation, in 1916, just a few months after Einstein formulated his equation; Einstein and Nathan Rosen explored them in the 1930s; and John Wheeler and his research group studied them extensively, by a variety of mathematical calculations, in the 1950s. However, none of the wormholes that had been found as solutions of Einstein’s equation, prior to my trip down Interstate 5 in 1985, was suitable for Carl Sagan’s novel, because none of them could be traversed safely. Each and everyone of them was predicted to evolve with time in a very peculiar way: The wormhole is created at some moment of time, opens up briefly, and then pinches off and disappears—and its total life span from creation to pinch-off is so short that nothing whatsoever (no person, no radiation, no signal of any sort) can travel through it, from one mouth to the other. Anything that tries will get caught and destroyed in the pinch-off. Figure 14.2 shows a simple example.
Like most of my physicist colleagues, I have been skeptical of wormholes for decades. Not only does Einstein’s field equation predict that wormholes live short lives if left to their own devices; their lives are made even shorter by random infalling bits of radiation: The radiation (according to calculations by Doug Eardley and Ian Redmount) gets accelerated to ultra-high energy by the wormhole’s gravity, and as the energized radiation bombards the wormhole’s throat, it triggers the throat to recontract and pinch off far faster than it would otherwise—so fast, in fact, that the wormhole has hardly any life at all.
There is another reason for skepticism. Whereas black holes are an inevitable consequence of stellar evolution (massive, slowly spinning stars, of just the sort that astronomers see in profusion in our galaxy, will implode to form black holes when they die), there is no analogous, natural way for a wormhole to be created. In fact, there is no reason at all to think that our Universe contains today any singularities of the sort that give birth to wormholes (Figure 14.2); and even if such singularities did exist, it is hard to understand how two of them could find each other in the vast reaches of hyperspace, so as to create a wormhole in the manner of Figure 14.2.
W hen one’s friend needs help, one is willing to turn most anywhere that help might be found. Wormholes—despite my skepticism about them—seemed to be the only help in sight. Perhaps, it occurred to me on Interstate 5 somewhere west of Fresno, there is some way that an infinitely advanced civilization could hold a wormhole open, that is, prevent it from pinching off, so that Eleanor Arroway could travel through it from Earth to Vega and back. I pulled out pen and paper and began to calculate. (Fortunately, Interstate 5 is very straight; I could calculate without getting carsick.)
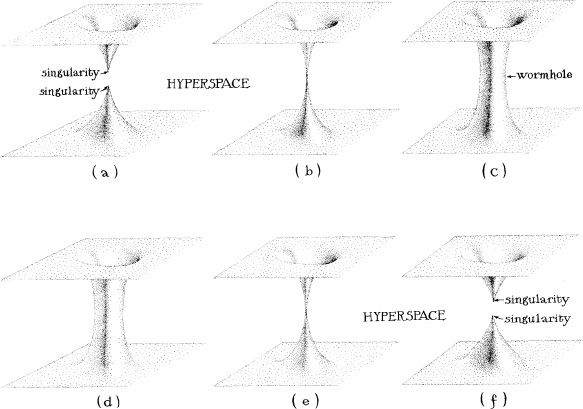
14.2 The evolution of a precisely spherical wormhole that has no material in its interior. (This evolution was discovered as a solution of Einstein’s field equation in the mid-1950s by Martin Kruskal, a young associate of Wheeler’s at Princeton University.) Initially (a) there is no wormhole; instead there is a singularity near Earth and one near Vega. Then, at some moment of time (b), the two singularities reach out through hyperspace, find each other, annihilate each other, and in the annihilation they create the wormhole. The wormhole grows in circumference (c), then begins to recontract (d), and pinches off (e), creating two singularities (f) similar to those in which the wormhole was born—but with one crucial exception. Each initial singularity (a) is like that of the big bang; time flows out of it, so it can give birth to something: the Universe in the case of the big bang, and the wormhole in this case. Each final singularity (f), by contrast, is like that of the big crunch ( Chapter 13 ); time flows into it, so things get destroyed in it: the Universe in the case of the big crunch, and the wormhole in this case. Anything that tries to cross through the wormhole during its brief life gets caught in the pinch-off and, along with the wormhole itself, gets destroyed in the final singularities (f).
To make the calculations easy, I idealized the wormhole as precisely spherical (so in Figure 14.1, where one of our Universe’s three dimensions is suppressed, it is precisely circular in cross section). Then, by two pages of calculations based on the Einstein field equation, I discovered three things:
First, the only way to hold the wormhole open is to thread the wormhole with some sort of material that pushes the wormhole’s walls apart, gravitationally. I shall call such material exotic because, as we shall see, it is quite different from any material that any human has ever yet met.
Second, I discovered that, just as the required exotic material must push the wormhole’s walls outward, so also, whenever a beam of light passes through the material, the material will gravitationally push outward on the beam’s light rays, prying them apart from each other. In other words, the exotic material will behave like a “defocusing lens”; it will gravitationally defocus the light beam. See Box 14.1.
Third, I learned from the Einstein field equation that, in order to gravitationally defocus light beams and gravitationally push the wormhole’s walls apart, the exotic material threading the wormhole must have a negative average energy density, as seen by a light beam traveling through it . This requires a bit of explanation. Recall that gravity (spacetime curvature) is produced by mass (Box 2.6) and that mass and energy are equivalent (Box 5.2, where the equivalence is embodied in Einstein’s famous equation E = Mc 2 ). This means that gravity can be thought of as produced by energy. Now, take the energy density of the material inside the wormhole (its energy per cubic centimeter), as measured by a light beam—that is, as measured by someone who travels through the wormhole at (nearly) the speed of light—and average that energy density along the light beam’s trajectory. The resulting averaged energy density must be negative in order for the material to be able to defocus the light beam and hold the wormhole open-that is, in order for the wormhole’s material to be “exotic.” 3
This does not necessarily mean that the exotic material has a negative energy as measured by someone at rest inside the wormhole. Energy density is a relative concept, not absolute; in one reference frame it may be negative, in another positive. The exotic material can have a negative energy density as measured in the reference frame of a light beam that travels through it, but a positive energy density as measured in the wormhole’s reference frame. Nevertheless, because almost all forms of matter that we humans have ever encountered have positive average energy densities in everyone’s reference frame, physicists have long suspected that exotic material cannot exist. Presumably the laws of physics forbid exotic material, we physicists have conjectured, but just how the laws of physics might do so was not at all clear.
Box 14.1
Holding a Wormhole Open: Exotic Material
Any spherical wormhole through which a beam of light can travel will gravitationally defocus the light beam . To see that this is so, imagine (as drawn below) that the beam is sent through a converging lens before it enters the wormhole, thereby making all its rays converge radially toward the wormhole’s center. Then the rays will always continue to travel radially (how else could they possibly move?), which means that when they emerge from the other mouth, they are diverging radially outward, away from the wormhole’s center, as shown. The beam has been defocused.
The wormhole’s spacetime curvature, which causes the defocusing, is produced by the “exotic” material that threads through the wormhole and holds the wormhole open. Since spacetime curvature is equivalent to gravity, it, in fact is the exotic material’s gravity that defocuses the light beam. In other words, the exotic material gravitationally repels the beam’s light rays, pushing them away from itself and hence away from each other, and thereby defocuses them.
This is precisely the opposite to what happens in a gravitational lens (Figure 8.2). There light from a distant star is focused by the gravitational pull of an intervening star or galaxy or black hole; here the light is defocused.
Perhaps our prejudice against the existence of exotic material is wrong, I thought to myself as I rode down Interstate 5. Perhaps exotic material can exist. This was the only way I could see to help Carl. So upon reaching Pasadena, I wrote Carl a long letter, explaining why his heroine could not use black holes for rapid interstellar travel, and suggesting that she use wormholes instead, and that somebody in the novel discover that exotic material can really exist and can be used to hold the wormholes open. Carl accepted my suggestion with pleasure and incorporated it into the final version of his novel, Contact. 4
I t occurred to me, after offering Carl Sagan my comments, that his novel could serve as a pedagogical tool for students studying general relativity. As an aid for such students, during the autumn of 1985 Mike Morris (one of my own students) and I began to write a paper on the general relativistic equations for wormholes supported by exotic material, and those equations’ connection to Sagan’s novel.
We wrote slowly. Other projects were more urgent and got higher priority. By the winter of 1987–88, we had submitted our paper to the American Journal of Physics , but it was not yet published; and Morris, nearing the end of his Ph.D. training, was applying for postdoctoral positions. With his applications, Morris enclosed the manuscript of our paper. Don Page (a professor at Pennsylvania State University and a former student of mine and Hawking’s) received the application, read our manuscript, and fired off a letter to Morris.
“Dear Mike, . . . it follows immediately from Proposition 9.2.8 of the book by Hawking- & Ellis, plus the Einstein field equations, that any wormhole [requires exotic material to hold it open] . . . Sincerely, Don N. Page.”
How stupid I felt. I had never studied global methods 5 (the topic of the Hawking and Ellis book) in any depth, and I was now paying the price. I had deduced on Interstate 5, with modest labor, that to hold a precisely spherical wormhole open one must thread it with exotic material. However, now, using global methods and with even less labor, Page had deduced that to hold any wormhole open (a spherical wormhole, a cubical wormhole, a wormhole with random deformations), one must thread it with exotic material. I later learned that Dennis Gannon and C. W. Lee reached almost the same conclusion in 1975.
T his discovery, that all wormholes require exotic material to hold them open, triggered much theoretical research during 1988–92. “Do the laws of physics permit exotic material to exist, and if so, under what circumstances?” This was the central issue.
A key to the answer had already been provided in the 1970s by Stephen Hawking. In 1970, when proving that the surface areas of black holes always increase (Chapter 12 ), Hawking had to assume that there is no exotic material near any black hole’s horizon. If exotic material were in the horizon’s vicinity, then Hawking’s proof would fail, his theorem would fail, and the horizon’s surface area could shrink. Hawking didn’t worry much about this possibility, however; it seemed in 1970 a rather safe bet that exotic material cannot exist.
Then, in 1974, came a great surprise: Hawking inferred as a by-product of his discovery of black-hole evaporation (Chapter 12 ) that vacuum fluctuations near a hole’s horizon are exotic: They have negative average energy density as seen by outgoing light beams near the hole’s horizon. In fact, it is this exotic property of the vacuum fluctuations that permits the hole’s horizon to shrink as the hole evaporates, in violation of Hawking’s area-increase theorem. Because exotic material is so important for physics, I shall explain this in greater detail:
Recall the origin and nature of vacuum fluctuations, as discussed in Box 12.4: When one tries to remove all electric and magnetic fields from some region of space, that is, when one tries to create a perfect vacuum, there always remain a plethora of random, unpredictable electromagnetic oscillations-oscillations caused by a tug-of-war between the fields in adjacent regions of space. The fields “here” borrow energy from the fields “there,” leaving the fields there with a deficit of energy, that is, leaving them momentarily with negative energy. The fields there then quickly grab the energy back and with it a little excess, driving their energy momentarily positive, and so it goes, onward and onward.
Under normal circumstances on Earth, the average energy of these vacuum fluctuations is zero. They spend equal amounts of time with energy deficits and energy excesses, and the average of deficit and excess vanishes. Not so near the horizon of an evaporating black hole, Hawking’s 1974 calculations suggested. Near a horizon the average energy must be negative, at least as measured by light beams, which means that the vacuum fluctuations are exotic.
How this comes about was not deduced in detail until the early 1980s, when Don Page at Pennsylvania State University, Philip Candelas at Oxford, and many other physicists used the laws of quantum fields in curved spacetime to explore in great detail the influence of a hole’s horizon on the vacuum fluctuations. They found that the horizon’s influence is key. The horizon distorts the vacuum fluctuations away from the shapes they would have on Earth, and by this distortion it makes their average energy density negative, that is, it makes the fluctuations exotic.
Under what other circumstances will vacuum fluctuations be exotic? Can they ever be exotic inside a wormhole, and thereby hold the wormhole open? This was the central thrust of the research effort triggered by Page’s noticing that the only way to hold any wormhole open is with exotic material.
The answer has not come easily, and is not entirely in hand. Gunnar Klinkhammer (a student of mine) has proved that in flat spacetime, that is, far from all gravitating objects, vacuum fluctuations can never be exotic—they can never have a negative average energy density as measured by light beams. On the other hand, Robert Wald (a former student of Wheeler’s) and Ulvi Yurtsever (a former student of mine) have proved that in curved spacetime, under a very wide variety of circumstances, the curvature distorts the vacuum fluctuations and thereby makes them exotic.
Is a wormhole that is trying to pinch off such a circumstance? Can the curvature of the wormhole, by distorting the vacuum fluctuations, make them exotic and enable them to hold the wormhole open? We still do not know, as this book goes to press.
I n early 1988, as theoretical studies of exotic material were getting under way, I began to recognize the power of the kind of research that Carl Sagan’s phone call had triggered. Just as among all real physics experiments that an experimenter might do the ones most likely to yield deep new insights into the laws of physics are those that push on the laws the hardest, then similarly, among all thought experiments that a theorist might study, when probing laws that are beyond the reaches of modern technology, the ones most likely to yield deep new insights are those that push the hardest. And no type of thought experiment pushes the laws of physics harder than the type triggered by Carl Sagan’s phone call to me—thought experiments that ask, “What things do the laws of physics permit an infinitely advanced civilization to do, and what things do the laws forbid? ” (By an “infinitely advanced civilization,” I mean one whose activities are limited only by the laws of physics, and not at all by ineptness, lack of know-how, or anything else.)
We physicists, I believe, have tended to avoid such questions because they are so close to science fiction. While many of us may enjoy reading science fiction or may even write some, we fear ridicule from our colleagues for working on research close to the science fiction fringe. We therefore have tended to focus on two other, less radical, types of questions: “What kinds of things occur naturally in the Universe?” (for example, do black holes occur naturally? and do wormholes occur naturally?). And “What kinds of things can we as humans, with our present or near-future technology, do?” (for example, can we produce new elements such as plutonium and use them to make atomic bombs? and can we produce high-temperature superconductors and use them to lower the power bills for levitated trains and Superconducting Supercollider magnets?).
By 1988 it seemed clear to me that we physicists had been much too conservative in our questions. Already, one Sagan-type question (as I shall call them) was beginning to bring a payoff. By asking, “Can an infinitely advanced civilization maintain wormholes for rapid interstellar travel?” Morris and I had identified exotic material as the key to wormhole maintenance, and we had triggered a somewhat fruitful effort to understand the circumstances under which the laws of physics do and do not permit exotic material to exist.
S uppose that our Universe was created (in the big bang) with no wormholes at all. Then eons later, when intelligent life has evolved and has produced a (hypothetical) infinitely advanced civilization, can that infinitely advanced civilization construct wormholes for rapid interstellar travel? Do the laws of physics permit wormholes to be constructed where previously there were none? Do the laws permit this type of change in the topology of our Universe’s space?
These questions are the second half of Carl Sagan’s interstellar transport problem. The first half , maintaining a wormhole once it has been constructed, Sagan solved with the help of exotic matter. The second half he finessed. In his novel, he describes the wormhole through which Eleanor Arroway traveled as now being maintained by exotic matter, but as having been created in the distant past by some infinitely advanced civilization, from which all records have been lost.
We physicists, of course, are not happy to relegate wormhole creation to prehistory. We want to know whether and how the Universe’s topology can be changed now , within the confines of physical law.
We can imagine two strategies for constructing a wormhole where before there was none: a quantum strategy , and a classical strategy.
The quantum strategy relies on gravitational vacuum fluctuations (Box 12.4), that is, the gravitational analogue of the electromagnetic vacuum fluctuations discussed above: random, probabilistic fluctuations in the curvature of space caused by a tug-of-war in which adjacent regions of space are continually stealing energy from each other and then giving it back. Gravitational vacuum fluctuations are thought to be everywhere, but under ordinary circumstances they are so tiny that no experimenter has ever detected them.
Just as an electron’s random degeneracy motions become more vigorous when one confines the electron to a smaller and smaller region (Chapter 4 ), so also gravitational vacuum fluctuations are more vigorous in small regions than in large, that is, for small wavelengths rather than for large. In 1955, John Wheeler, by combining the laws of quantum mechanics and the laws of general relativity in a tentative and crude way, deduced that in a region the size of the Planck–Wheeler length , 6 1.62 × 10 –33 centimeter or smaller, the vacuum fluctuations are so huge that space as we know it “boils” and becomes a froth of quantum foam—the same sort of quantum foam as makes up the core of a spacetime singularity (Chapter 13 ; Figure 14.3).
Quantum foam, therefore, is everywhere: inside black holes, in interstellar space, in the room where you sit, in your brain. But to see the quantum foam, one would have to zoom in with a (hypothetical) supermicroscope, looking at space and its contents on smaller and smaller scales. One would have to zoom in from the scale of you and me (hundreds of centimeters) to the scale of an atom (10 −8 centimeter), to the scale of an atomic nucleus (10 −13 centimeter), and then on downward by twenty factors of 10 more, to 10 −33 centimeter. At all the early, “large” scales, space would look completely smooth, with a very definite (but tiny) amount of curvature. As the microscopic zoom nears, then passes 10 −32 centimeter, however, one would see space begin to writhe, ever so slightly at first, and then more and more strongly until, when a region just 10 −33 centimeter in size fills the supermicroscope’s entire eyepiece, space has become a froth of probabilistic quantum foam.
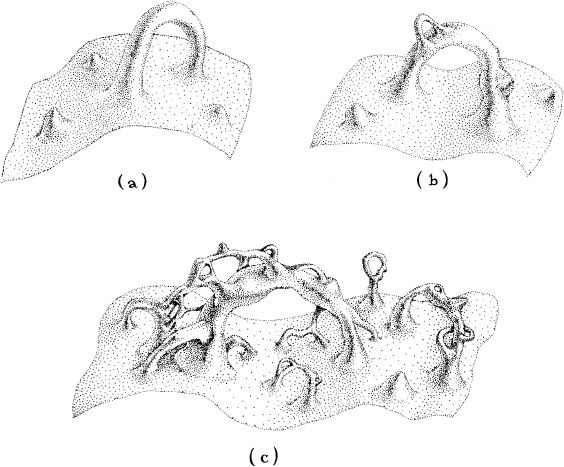
14.3 (Same as Figure 13.7.) Embedding diagrams illustrating quantum foam. The geometry and topology of space are not definite; instead, they are probabilistic. They might have, for example, a 0.1 percent probability for the form shown in (a), a 0.4 percent probability for (b), a 0.02 percent probability for (c), and so on.
Since the quantum foam is everywhere, it is tempting to imagine an infinitely advanced civilization reaching down into the quantum foam, finding in it a wormhole (say, the “big” one in Figure 14.3b with its 0.4 percent probability), and trying to grab that wormhole and enlarge it to classical size. In 0.4 percent of such attempts, if the civilization were truly infinitely advanced, they might succeed. Or would they?
We do not yet understand the laws of quantum gravity well enough to know. One reason for our ignorance is that we do not understand the quantum foam itself very well. We aren’t even 100 percent sure it exists. However, the challenge of this Sagan—type thought experiment—an advanced civilization pulling wormholes out of the quantum foam—might be of some conceptual help in the coming years, in efforts to firm up our understanding of quantum foam and quantum gravity.
So much for the quantum strategy of wormhole creation. What is the classical strategy?
In the classical strategy, our infinitely advanced civilization would try to warp and twist space on macroscopic scales (normal, human scales) so as to make a wormhole where previously none existed. It seems fairly obvious that, in order for such a strategy to succeed, one must tear two holes in space and sew them together. Figure 14.4 shows an example.
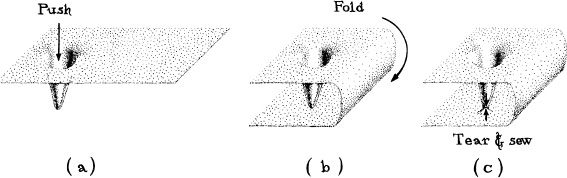
14.4 One strategy for making a wormhole. (a) A “sock” is created in the curvature of space. (b) Space outside the sock is gently folded in hyperspace. (c) A small hole is torn in the toe of the sock, a hole is torn in space just below the hole, and the edges of the holes are “sewn” together. This strategy looks classical (macroscopic) at first sight. However, the tearing produces, at least momentarily, a spacetime singularity which is governed by the laws of quantum gravity, so this strategy is really a quantum one.
Now, any such tearing of space produces, momentarily, at the point of the tear, a singularity of spacetime, that is, a sharp boundary at which spacetime ends; and since singularities are governed by the laws of quantum gravity, such a strategy for making wormholes is actually quantum mechanical, not classical. We will not know whether it is permitted until we understand the laws of quantum gravity.
Is there no way out? Is there no way to make a wormhole without getting entangled with the ill-understood laws of quantum gravity—no perfectly classical way?
Somewhat surprisingly, there is —but only if one pays a severe price. In 1966, Robert Geroch (a student of Wheeler’s at Princeton) used global methods to show that one can construct a wormhole by a smooth, singularity-free warping and twisting of spacetime, but one can do so only if, during the construction, time also becomes twisted up as seell in all reference frames. 7 More specifically, while the construction is going on, it must be possible to travel backward in time, as well as forward; the “machinery” that does the construction, whatever it might be, must function briefly as a time machine that carries things from late moments of the construction back to early moments (but not back to moments before the construction began).
The universal reaction to Geroch’s theorem, in 1967, was “Surely the laws of physics forbid time machines, and thereby they will prevent a wormhole from ever being constructed classically, that is, without tearing holes in space.”
In the decades since 1967, some things we thought were sure have been proved wrong. (For example, we would never have believed in 1967 that a black hole can evaporate.) This has taught us caution. As part of our caution, and triggered by Sagan-type questions, we began asking in the late 1980s, “Do the laws of physics really forbid time machines, and if so, how? How might the laws enforce such a prohibition?” To this question I shall return below.
L et us now pause and take stock. In 1993 our best understanding of wormholes is this:
If no wormholes were made in the big bang, then an infinitely advanced civilization might try to construct one by two methods, quantum (pulling it out of the quantum foam) or classical (twisting spacetime without tearing it). We do not understand the laws of quantum gravity well enough to deduce, in 1993, whether the quantum construction of wormholes is possible. We do understand the laws of classical gravity (general relativity) well enough to know that the classical construction of wormholes is permitted only if the construction machinery, whatever it might be, twists time up so strongly, as seen in all reference frames, that it produces, at least briefly, a time machine.
We also know that, if an infinitely advanced civilization somehow acquires a wormhole, then the only way to hold the wormhole open (so it can be used for interstellar travel) is by threading it with exotic material. We know that vacuum fluctuations of the electromagnetic field are a promising form of exotic material: They can be exotic (have a negative average energy density as measured by a light beam) in curved spacetime under a wide variety of circumstances. However, we do not yet know whether they can be exotic inside a wormhole and thereby hold the wormhole open.
In the pages to come, I shall assume that an infinitely advanced civilization has somehow acquired a wormhole and is holding it open by means of some sort of exotic material; and I shall ask what other uses, besides interstellar travel, the civilization might find for its wormhole.
Time Machines
I n December 1986, the fourteenth semi-annual Texas Symposium on Relativistic Astrophysics was held in Chicago, Illinois. These “Texas” symposia, patterned after the 1963 one in Dallas, Texas, where the mystery of quasars was first discussed (Chapters 7 and 9 ), had by now become a firmly established institution. I went to the symposium and lectured on dreams and plans for LIGO (Chapter 10 ). Mike Morris (my “wormhole” student) also went, to get his first full-blown exposure to the international community of relativity physicists and astrophysicists.
In the corridors between lectures, Morris became acquainted with Tom Roman, a young assistant professor from Central Connecticut State University who, several years earlier, had produced deep insights about exotic matter. Their conversation quickly turned to wormholes. “If a wormhole can really be held open, then it will permit one to travel over interstellar distances far faster than light,” Roman noted.
“Doesn’t this mean that one can also use a wormhole to travel backward in time?”
How stupid Mike and 1 felt! Of course; Roman was right. We, in fact, had learned about such time travel in our childhoods from a famous limerick:
There once was a lady named Bright
who traveled much faster than light.
She departed one day in a relative way
and came home the previous night.
With Roman’s comment and the famous limerick to goad us, we easily figured out how to construct a time machine using two wormholes that move at high speeds relative to each other. 8 (I shall not describe that time machine here, because it is a bit complicated and there is a simpler, more easily described time machine to which I shall come shortly.)
I am a loner; I like to retreat to the mountains or an isolated seacoast, or even just into an attic, and think. New ideas come slowly and require large blocks of quiet, undisturbed time to gestate; and most worthwhile calculations require days or weeks of intense, steady concentration. A phone call at the wrong moment can knock my concentration off balance, setting me back by hours. So I hide from the world.
But hiding for too long is dangerous. I need, from time to time, the needle-pricking stimulus of conversations with people whose viewpoints and expertise are different from mine.
In this chapter thus far I have described three examples. Without Carl Sagan’s phone call and the challenge to make his novel scientifically correct, I would never have ventured into research on wormholes and time machines. Without Don Page’s letter, Mike Morris and I would not have known that all wormholes, regardless of their shape, require exotic material to keep them open. And without Tom Roman’s remark, Morris and I might have gone on blithely unaware that from wormholes an advanced civilization can easily make a time machine.
In the pages to come, I will describe other examples of the crucial role of needle-pricking interactions. However, not all ideas arise that way. Some arise from introspection. June 1987 was a case in point.
In early June 1987, emerging from several months of frenetic class-room teaching and interactions with my research group and the LIGO team, I retreated, exhausted, into isolation.
All spring long something had been gnawing at me, and I had been trying to ignore it, waiting for some days of quiet, to ponder. Those days, at last, had come. In isolation, I let the gnawing emerge from my subconscious and began to examine it: “How does time decide how to hook itself up through a wormhole? ” That was the nub of the gnaw.
To make this question more concrete, I thought about an example: Suppose that I have a very short wormhole, one whose tunnel through hyperspace is only 30 centimeters long, and suppose that both mouths of the wormhole—two spheres, each 2 meters in diameter—are sitting in my Pasadena living room. And suppose that I climb through the wormhole, head first. From my viewpoint, I must emerge from the second mouth immediately after I enter the first, with no delay at all; in fact, my head is coming out of the second mouth while my feet are still entering the first. Does this mean that my wife, Carolee, sitting there on the living room sofa, will also see my head emerging from the second mouth while my feet are still climbing into the first, as in Figure 14.5? If so, then time “hooks up through the wormhole” in the same manner as it hooks up outside the wormhole.

14.5 A picture of me crawling through a hypothetical, very short wormhole.
On the other hand, I asked myself, isn’t it possible that, although the trip through the wormhole takes almost no time as seen by me, Carolee must wait an hour before she sees me emerge from the second mouth; and isn’t it also possible that she sees me emerge an hour before I entered? If so, then time would be hooked up through the wormhole in a different manner than it hooks up outside the wormhole.
What could possibly make time behave so weirdly? I asked myself. On the other hand, why shouldn’t it behave in this way? Only the laws of physics know the answer, I reasoned. Somehow, I ought to be able to deduce from the laws of physics just how time will behave.
As an aid to understanding how the laws of physics control time’s hookup, I thought about a more complicated situation. Suppose that one mouth of the wormhole is at rest in my living room and the other is in interstellar space, traveling away from Earth at nearly the speed of light. And suppose that, despite this relative motion of its two mouths, the wormhole’s length (the length of its tunnel through hyperspace) remains always fixed at 30 centimeters. (Figure 14.6 explains how it is possible for the length of the wormhole to remain fixed while its mouths, as seen in the external Universe, move relative to each other.) Then, as seen in the external Universe, the two mouths are in different reference frames, frames that move at a high speed relative to each other; and the mouths therefore must experience different flows of time. On the other hand, as seen through the wormhole’s interior, the mouths are at rest with respect to each other, so they share a common reference frame, which means that the mouths must experience the same flow of time . From the external viewpoint they experience different time flows, and from the internal viewpoint, the same time flow; how confusing!

14.6 Explanation of how the mouths of a wormhole can move relative to each other as seen in the external Universe, while the length of the wormhole remains fixed. Each of the diagrams is an embedding diagram like that in Figure 14.1, seen in profile. The diagrams are a sequence of snapshots that depict motion of the Universe and the wormhole relative to hyperspace . (Recall, however, that hyperspace is just a useful figment of our imaginations; there is no way that we as humans can ever see or experience it in reality; see Figures 3.2 and 3.3.) Relative to hyperspace, the bottom part of our Universe is sliding rightward in the diagrams, while the wormhole and the top part of our Universe remain at rest. Correspondingly, as seen in our Universe, the mouths of the wormhole are moving relative to each other (they are getting farther apart), but as seen through the wormhole they are at rest with respect to each other; the wormhole’s length does not change.
Gradually, in my quiet isolation, the confusion subsided and all became clear. The laws of general relativity predict, unequivocally, the flow of time at the two mouths, and they predict, unequivocally, that the two time flows will be the same when compared through the wormhole, but will be different when compared outside the wormhole. Time, in this sense, hooks up to itself differently through the wormhole than through the external Universe, when the two mouths are moving relative to each other.
And this difference of hookup, I then realized, implies that from a single wormhole, an infinitely advanced civilization can make a time machine. There is no need for two wormholes. How? Easy, if you are infinitely advanced.
To explain how, I shall describe a thought experiment in which we humans are infinitely advanced beings. Carolee and I find a very short wormhole, and put one of its mouths in the living room of our home and the other in our family spacecraft, outside on the front lawn.
Now, as this thought experiment will show, the manner in which time is hooked up through any wormhole actually depends on the wormhole’s past history. For simplicity, I shall assume that when Carolee and I first acquire the wormhole, it has the simplest possible hookup of time: the same hookup through the wormhole’s interior as througll the exterior Universe. In other words, if I climb through the wormhole, Carolee, I, and everyone on Earth will agree that I emerge from the mouth in the spacecraft at essentially the same moment as I entered the mouth in the living room.
Having checked that time is, indeed, hooked up through the wormhole in this way, Carolee and I then make a plan: I will stay at home in our living room with the one mouth, while Carolee in our spacecraft takes the other mouth on a verv high speed trip out into the Universe and back. Throughout the trip, we will hold hands through the wormhole; see Figure 14.7.
14.7 Carolee and I construct a time machine from a wormhole. Left: I stay at home in Pasadena with one mouth of the wormhole and hold hands with Carolee through the wormhole. Right: Carolee carries the other mouth on a high-speed trip through the Universe. Inset: Our hands inside the wormhole.
Carolee departs at 9:00 A.M. on 1 January 2000, as measured by herself, by me, and by everybody else on Earth. Carolee zooms away from Earth at nearly the speed of light for 6 hours as measured by her own time; then she reverses course and zooms back, arriving on the front lawn 12 hours after her departure as measured by her own time. 9 I hold hands with her and watch her through the wormhole throughout the trip, so obviously I agree, while looking through the wormhole , that she has returned after just 12 hours, at 9:00 P.M. on 1 January 2000. Looking through the wormhole at 9:00 P.M., I can see not only Carolee; I can also see, behind her, our front lawn and our house.
Then, at 9:01 P.M., I turn and look out the window—and there I see an empty front lawn. The spaceship is not there; Carolee and the other wormhole mouth are not there. Instead, if I had a good enough telescope pointed out the window, I would see Carolee’s spaceship flying away from Earth on its outbound journey, a journey that as measured on Earth, looking through the external Universe , will require 10 years. [This is the standard “twins paradox”; the high-speed “twin” who goes out and comes back (Carolee) measures a time lapse of only 12 hours, while the “twin” who stays behind on Earth (me) must wait 10 years for the trip to be completed.]
I then go about my daily routine of life. For day after day, month after month, year after year, I carry on with life, waiting—until finally, on 1 January 2010, Carolee returns from her journey and lands on the front lawn. I go out to meet her, and find, as expected, that she has aged just 12 hours, not 10 years. She is sitting there in the spaceship, her hand thrust into the wormhole mouth, holding hands with somebody. I stand behind her, look into the mouth, and see that the person whose hand she holds is myself, 10 years younger, sitting in our living room on 1 January 2000. The wormhole has become a time machine. If I now (on 1 January 2010) climb into the wormhole mouth in the spaceship, I will emerge through the other mouth in our living room on 1 January 2000, and there I will meet my younger self. Similarly, if my younger self climbs into the mouth in the living room on 1 January 2000, he will emerge from the mouth in the spaceship on 1 January 2010. Travel through the wormhole in one direction takes me backward 10 years in time; travel in the other direction takes me 10 years forward.
Neither I nor anyone else, however, can use the wormhole to travel back in time beyond 9:00 P.M., 1 January 2000. It is impossible to travel to a time earlier than when the wormhole first became a time machine.
The laws of general relativity are unequivocal. If wormholes can be held open by exotic material, then these are general relativity’s predictions.
I n summer 1987, a month or so after I arrived at these predictions, Richard Price telephoned Carolee. Richard—a close friend of mine and the man who sixteen years earlier had shown that a black hole radiates away all its “hair” (Chapter 7 )—was worried about me. He had heard that I was working on the theory of time machines, and he feared I had gone a little crazy or senile or. . . Carolee tried to reassure him.
Richard’s call shook me up a bit. Not because I doubted my own sanity; I had few doubts. However, if even my closest friends were worried, then (at least as a protection for Mike Morris and my other students, if not for myself) I would have to be careful about how we presented our research to the community of physicists and to the general public.
During the winter of 1987–88, as part of my caution, I decided to move slowly on publishing anything about time machines. Together with two students, Mike Morris and Ulvi Yurtsever, I focused on trying to understand everything I could about wormholes and time. Only after all issues were crystal clear did I want to publish.
Morris, Yurtsever, and I worked together by computer link and telephone, since I was hiding in isolation. Carolee had taken a two-year postdoctoral appointment in Madison, Wisconsin, and I had gone along as her “house husband” for the first seven months (January–July 1988). I had set up my computer and working tables in the attic of the house we rented in Madison; and I was spending most of my waking hours there in the attic, thinking, calculating, and writing—largely on other projects, but partly on wormholes and time.
For stimulus and to test my ideas against skilled “opponents,” every few weeks I drove over to Milwaukee to talk with a superb group of relativity researchers led by John Friedman and Leonard Parker, and occasionally I drove down to Chicago to talk with another superb group led by Subrahmanyan Chandrasekhar, Robert Geroch, and Robert Wald.
On a March visit to Chicago, I got a jolt. I gave a seminar describing everything I understood about wormholes and time machines; and after the seminar, Geroch and Wald asked me (in effect), “Won’t a wormhole be automatically destroyed whenever an advanced civilization tries to convert it into a time machine?”
Why? How? I wanted to know. They explained. Translated into the language of the Carolee-and-me story, their explanation was the following: Imagine that Carolee is zooming back to Earth with one wormhole mouth in her spacecraft and I am sitting at home on Earth with the other. Shortly after she turns around and begins zooming home, it suddenly becomes possible for radiation (electromagnetic waves) to use the wormhole for time travel: Any random bit of radiation that leaves our home in Pasadena traveling at the speed of light toward her spacecraft can arrive at the spacecraft after 5 years’ time (as seen on Earth), enter the wormhole mouth there, travel back in time by 5 years (as seen on Earth), and emerge from the mouth on Earth at precisely the same moment as it started its trip. The radiation piles right on top of its previous self, not just in space but in spacetime, doubling its strength. What’s more, during the trip each quantum of radiation (each photon) got boosted in energy due to the relative motion of the wormhole mouths (a “Doppler-shift” boost).
After the radiation’s next trip out to the spacecraft then back through the wormhole, it again returns at the same time as it left and again piles up on itself, again with a Doppler-boosted energy. Again and again this happens, making the beam of radiation infinitely strong (Figure 14.8a).
14.8 (a) The Geroch-Wald suggestion for how a wormhole might get destroyed when one tries to make it into a time machine. An intense beam of radiation zooms between the two mouths and through the wormhole, piling up on and reinforcing itself. The beam becomes infinitely energetic and destroys the wormhole. (b) What actually happens. The wormhole defocuses the beam, reducing the amount of pileup. The beam remains weak; the wormhole is not destroyed.
In this way, beginning with an arbitrarily tiny amount of radiation, a beam of infinite energy is created, coursing through space between the two wormhole mouths. As the beam passes through the wormhole, Geroch and Wald argued, it will produce infinite spacetime curvature and probably destroy the wormhole, thereby preventing the wormhole from becoming a time machine.
I drove away from Chicago and up Interstate 90 toward Madison in a daze. My mind was filled with geometric pictures of radiation beams shooting from one wormhole mouth to the other, as the mouths move toward each other. I was trying to compute, pictorially, just what would happen. I was trying to understand whether Geroch and Wald were right or wrong.
Gradually, as I neared the Wisconsin border, the pictures in my mind became clear. The wormhole would not be destroyed. Geroch and Wald had overlooked a crucial fact: Every time the beam of radiation passes through the wormhole, the wormhole defocuses it in the manner of Box 14.1 above. After the defocusing, the beam emerges from the mouth on Earth and spreads out over a wide swath of space, so that only a tiny fraction of it can get caught by the mouth on the spacecraft and transported through the wormhole back to Earth to “pile up” on itself (Figure 14.8b).
I could do the sum visually in my head, as I drove. By adding up all the radiation from all the trips through the wormhole (a tinier and tinier amount after each defocusing trip), I computed that the final beam would be weak; far too weak to destroy the wormhole.
My calculation turned out to be right; but, as I shall explain later, I should have been more cautious. This brush with wormhole destruction should have warned me that unexpected dangers await any maker of time machines.
W hen graduate students reach the final year of their research, they often give me great pleasure. They produce major insights on their own; they argue with me and win; they teach me unexpected things. Such was the case with Morris and Yurtsever as we gradually moved toward finalizing our manuscript for Physical Review Letters . Large portions of the manuscript’s technical details and technical ideas were theirs.
As our work neared completion, I oscillated between worrying about tarnishing Morris’s and Yurtsever’s budding scientific reputations with a label of “crazy science fiction physicists” and waxing enthusiastic about the things we had learned and about our realization that Sagan-type questions can be powerful in physics research. At the last minute, as we finalized the paper, I suppressed my caution (which Morris and Yurtsever seemed not to share), and agreed with them to give our paper the title “Wormholes, Time Machines, and the Weak Energy Condition” (“weak energy condition” being the technical term associated with “exotic matter”).
Despite the “time machines” in the title, our paper was accepted for publication without question. The two anonymous referees seemed to be sympathetic; I heaved a sigh of relief.
With the publication date nearing, caution took hold of me again; I asked the staff of the Caltech Public Relations Office to avoid and, indeed, try to suppress any and all publicity about our time machine research. A sensational splash in the press might brand our research as crazy in the eyes of many physicists, and I wanted our paper to be studied seriously by the physics community. The public relations staff acquiesced.
Our paper was published, and all went well. As I had hoped, the press missed it, but among physicists it generated interest and controversy. Letters trickled in, asking questions and challenging our claims; but we had done our homework. We had answers.
My friends’ reactions were mixed. Richard Price continued to worry; he had decided I wasn’t crazy or senile, but he feared I would sully my reputation. My Russian friend Igor Novikov, by contrast, was ecstatic. Telephoning from Santa Cruz, California, where he was visiting, Novikov said, “I’m so happy, Kip! You have broken the barrier. If you can publish research on time machines, then so can I! ” And he proceeded to do so, forthwith.
The Matricide Paradox
A mong the controversies stirred up by our paper, the most vigorous was over what I like to call the matricide paradox 10 : If I have a time machine (wormhole-based or otherwise), I should be able to use it to go back in time and kill my mother before I was conceived, thereby preventing myself from being born and killing my mother. 11
Central to the matricide paradox is the issue of free will: Do I, or do I not, as a human being, have the power to determine my own fate? Can I really kill my mother, after going backward in time, or (as in so many science fiction stories) will something inevitably stay my hand as I try to stab her in her sleep?
Now, even in a universe without time machines, free will is a terribly difficult thing for physicists to deal with. We usually try to avoid it. It just confuses issues that otherwise might be lucid. With time machines, all the more so. Accordingly, before publishing our paper (but after long discussions with our Milwaukee colleagues), Morris, Yurtsever, and I decided to avoid entirely the issue of free will. We insisted on not discussing at all, in print, human beings who go through a wormhole-based time machine. Instead, we dealt only with simple, inanimate time-traveling things, such as electromagnetic waves.
Before publishing, we thought a lot about waves that travel backward in time through a wormhole; we searched hard for unresolvable paradoxes in the waves’ evolution. Ultimately (and with crucial proddings from John Friedman), we convinced ourselves that there probably will be no unresolvable paradoxes , and we conjectured so in our paper. 12 We even broadened our conjecture to suggest that there would never be unresolvable paradoxes for any inanimate object that passes through the wormhole. It was this conjecture that created the most controversy.
Of the letters we received, the most interesting was from Joe Polchinski, a professor of physics at the University of Texas in Austin. Polchinski wrote, “Dear Kip, . . . If I understand correctly, you are conjecturing that in your [wormhole-based time machine there will be no unresolvable paradoxes]. It seems to me that . . . this is not the case.” He then posed an elegant and simple variant of the matricide paradox—a variant that is not entangled with free will and that we therefore felt competent to analyze:
Take a wormhole that has been made into a time machine, and place its two mouths at rest near each other, out in interplanetary space (Figure 14.9). Then, if a billiard ball is launched toward the right mouth from an appropriate initial location and with an appropriate initial velocity, the ball will enter the right mouth, travel backward in time, and fly out of the left mouth before it entered the right (as seen by you and me outside the wormhole), and it will then hit its younger self, thereby preventing itself from ever entering the right mouth and hitting itself.
This situation, like the matricide paradox, entails going back in time and changing history. In the matricide paradox, I go back in time and, by killing my mother, prevent myself from being born. In Polchinski’s paradox, the billiard ball goes back in time and, by hitting itself, prevents itself from ever going back in time.
Both situations are nonsensical. Just as the laws of physics must be logically consistent with each other, so also the evolution of the Universe, as governed by the laws of physics, must be fully consistent with itself—or at least it must be so when the Universe is behaving classically (non–quantum mechanically); the quantum mechanical realm is a little more subtle. Since both I and a billiard ball are highly classical objects (that is, we can exhibit quantum mechanical behavior only when one makes exceedingly accurate measurements on us; see Chapter 10 ), there is no way that either I or the billiard ball can go back in time and change our own histories.
14.9 Polchinski’s billiard ball version of the matricide paradox. The wormhole is very short and has been made into a time machine, so that anything that enters the right mouth emerges, as measured on the outside, 30 minutes before it went in. The flow of time outside the mouth is denoted by the symbol t; the flow of time as experienced by the billiard ball itself is denoted by τ. The billiard ball is launched at t = 3:00 P.M. from the indicated location and with just the right velocity to enter the right mouth at t = 3:45. The ball emerges from the left mouth 30 minutes earlier, at t = 3:15, and then hits its younger self at t = 3:30 P.M., knocking itself off track so it cannot enter the right mouth and hit itself.
So what happens to the billiard ball? To find out, Morris, Yurtsever, and I focused our attention on the ball’s initial conditions , that is, its initial location and velocity. We asked ourselves, “For the same initial conditions as led to Polchinski’s paradox, is there any other billiard ball trajectory that, unlike the one in Figure 14.9, is a logically self-consistent solution to the physical laws that govern classical billiard balls?” After much discussion, we agreed that the answer was probably “yes,” but we were not absolutely sure—and there was no time for us to figure it out. Morris and Yurtsever had completed their Ph.D.s and were leaving Caltech to take up postdoctoral appointments in Milwaukee and Trieste.
F ortunately, Caltech continually draws great students. There were two new ones waiting in the wings: Fernando Echeverria and Gunnar Klinkhammer. Echeverria and Klinkhammer took Polchinski’s paradox and ran with it: After some months of on-and-off mathematical struggle, they proved that there indeed is a fully self-consistent billiard ball trajectory that begins with Polchinski’s initial data and satisfies all the laws of physics that govern classical billiard balls. In fact, there are two such trajectories. They are shown in Figure 14.10. I shall describe each of these trajectories in turn, from the viewpoint of the ball itself.
On trajectory (a) (left half of Figure 14.10), the ball, young, clean, and pristine, starts out at time t = 3:00 P.M., moving along precisely the same route as in Polchinski’s paradox (Figure 14.9), a route taking it toward the wormhole’s right mouth. A half hour later, at t = 3:30, the young, pristine ball gets hit on its left, rear side , by an older-looking, cracked ball (which will turn out to be its older self). The collision is gentle enough to deflect the young ball only slightly from its original course, but hard enough to crack it. The young ball, now cracked, continues onward along its slightly altered trajectory and enters the wormhole mouth at t = 3:45, travels backward in time by 30 minutes, and exits from the other mouth at t = 3:15. Because its trajectory has been altered slightly by comparison with Polchinski’s paradoxical trajectory (Figure 14.9), the ball, now old and cracked, hits its younger self a gentle, glancing blow on the left, rear side at t = 3:30, instead of the vigorous, highly deflecting blow of Figure 14.9. The evolution thereby is made fully self-consistent.
Trajectory (b), the right half of Figure 14.10, is the same as (a), except that the geometry of the collision is slightly different, and correspondingly the trajectory between collisions is slightly different. In particular, the old, cracked ball emerges from the left mouth on a different trajectory than in (a), a trajectory that takes it in front of the young, pristine ball (instead of behind it), and produces a glancing blow on the young ball’s front, right side (instead of left rear side).
Echeverria and Klinkhammer showed that both trajectories, (a) and (b), satisfy all the physical laws that govern classical billiard balls, so both are possible candidates to occur in the real Universe (if the real Universe can have wormhole-based time machines).
This is most disquieting. Such a situation can never occur in a universe without time machines. Without time machines, each set of initial conditions for a billiard ball gives rise to one and only one trajectory that satisfies all the classical laws of physics. There is a unique prediction for the ball’s motion. The time machine has ruined this. There now are two, equally good predictions for the ball’s motion.
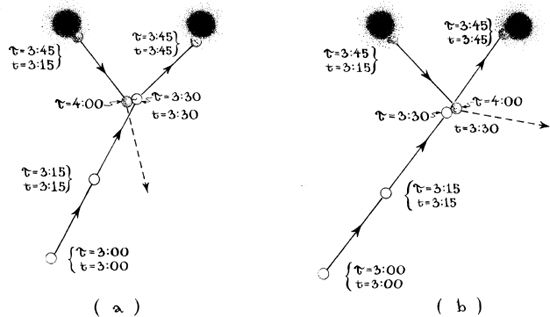
14.10 The resolution of Polchinski’s version of the matricide paradox (Figure 14.9): A billiard ball, starting out at 3:00 P.M. with the same initial conditions (same location and velocity) as in Polchinski’s paradox, can move along either of the two trajectories shown here. Each of these trajectories is fully self-consistent and satisfies the classical laws of physics everywhere along the trajectory.
Actually, the situation is even worse than it looks at first sight: The time machine makes possible an infinite number of equally good predictions for the ball’s motion, not just two. Box 14.2 shows a simple example.
Box 14.2
The Billiard Ball Crisis: An Infinity of Trajectories
One day, while sitting in San Francisco Airport waiting for a plane, it occurred to me that, if a billiard ball is fired between the two mouths of a wormhole-based time machine, there are two trajectories on which it can travel. On one (a), it hurtles between the mouths unscathed. On the other (b), as it is passing between the two mouths, it gets hit and knocked rightward, toward the right mouth; it then goes down the wormhole, emerges from the left mouth before it went down, hits itself, and flies away.

Some months later, Robert Forward [one of the pioneers of laser interferometer gravitational-wave detectors ( Chapter 10 ) and also a science fiction writer] discovered a third trajectory that satisfies all the laws of physics, the trajectory (c) below: The collision, instead of occurring between the mouths, occurs before the ball reaches the mouths’ vicinity. I then realized that the collision could be made to occur earlier and earlier, as in (d) and (e), if the ball travels through the wormhole several times between its two visits to the collision event. For example, in (e), the ball travels up route α, gets hit by its older self and knocked along β and into the right mouth; it then travels through the wormhole (and backward in time), emerging from the left mouth on γ, which takes it through the wormhole again (and still farther back in time), emerging along δ, which takes it through the wormhole yet again (and even farther back in time), emerging along ε, which takes it to the collision event, from which it is deflected down ζ.
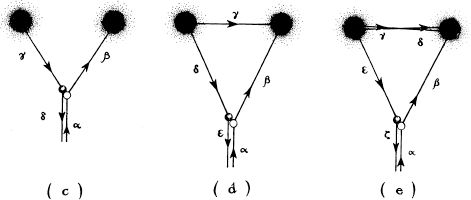
Evidently, there are an infinite number of trajectories (each with a different number of wormhole traversals) that all satisfy the classical (non-quantum) laws of physics, and all begin with identically the same initial conditions (the same initial billiard ball location and velocity). One is left wondering whether physics has gone crazy, or whether, instead, the laws of physics can somehow tell us which trajectory the ball ought to take.
D o time machines make physics go crazy? Do they make it impossible to predict how things evolve? If not, then how do the laws of physics choose which trajectory, out of the infinite allowed set, a billiard ball will follow?
In search of an answer, Gunnar Klinkhammer and I in 1989 turned from the classical laws of physics to the quantum laws. Why the quantum laws? Because they are the Ultimate Rulers of our Universe.
For example, the laws of quantum gravity have ultimate control over gravitation and the structure of space and time. Einstein’s classical, general relativistic laws of gravity are mere approximations to the quantum gravity laws—approximations with excellent accuracy when one is far from all singularities and looks at spacetime on scales far larger than 10 −33 centimeter, but approximations nevertheless (Chapter 13 ).
Similarly, the classical laws of billiard ball physics, which my students and I had used in studying Polchinski’s paradox, are mere approximations to the quantum mechanical laws. Since the classical laws seem to predict “nonsense” (an infinity of possible billiard ball trajectories), Klinkhammer and I turned to the quantum mechanical laws for deeper understanding.
The “rules of the game” are very different in quantum physics than in classical physics. When one provides the classical laws with initial conditions, they predict what will happen afterward (for example, what trajectory a ball will follow); and, if there are no time machines, their predictions are unique. The quantum laws, by contrast, predict only probabilities for what will happen, not certainties (for example, the probability that a ball will travel through this, that, or another region of space).
In light of these rules of the quantum mechanical game, the answer that Klinkhammer and I got from the quantum mechanical laws is not surprising. We learned that, if the ball starts out moving along Polchinski’s paradoxical trajectory (Figures 14.9 and 14.10 at time t = 3:00 P.M.), then there will be a certain quantum mechanical probability—say, 48 percent—for it subsequently to follow trajectory Ca) in Figure 14.10, and a certain probability-say, also 48 percent—for trajectory (b), and a certain (far smaller) probability for each of the infinity of other classically allowed trajectories. In anyone “experiment,” the ball will follow just one of the trajectories that the classical laws allow; but if we perform a huge number of identical billiard ball experiments, in 48 percent of them the ball will follow trajectory (a), in 48 percent trajectory (b), and so forth.
This conclusion is somewhat satisfying. It suggests that the laws of physics might accommodate themselves to time machines fairly nicely. There are surprises, but there seem not to be any outrageous predictions, and there is no sign of any unresolvable paradox. Indeed, the National Enquirer, hearing of this, could easily display a banner headline: PHYSICISTS PROVE TIME MACHINES EXIST. (That kind of outrageous distortion, of course, has been my recurrent fear.)
I n the autumn of 1988, three months after the publication of our paper “Wormholes, Time Machines, and the Weak Energy Condition,” Keay Davidson, a reporter for the San Francisco Examiner, discovered it in Physical Review Letters and broke the story.
It could have been worse. At least the physics community had had three months of quiet in which to absorb our ideas without the blare of sensational headlines.
But the blare was unstoppable. PHYSICISTS INVENT TIME MACHINES, read a typical headline. California magazine, in an article on “The Man Who Invented Time Travel,” even ran a photograph of me doing physics in the nude on Palomar Mountain. I was mortified—not by the photo, but by the totally outrageous claims that I had invented time machines and time travel. If time machines are, in fact, allowed by the laws of physics (and, as will become clear at the end of the chapter, I doubt that they are), then they are probably much farther beyond the human race’s present technological capabilities than space travel was beyond the capabilities of cavemen.
After talking with two reporters, I abandoned all efforts to stem the tide and get the story told accurately, and went into hiding. My besieged administrative assistant, Pat Lyon, had to fend off the press with a firm “Professor Thorne believes it is too early in this research effort to communicate results to the general public. When he feels he has a better understanding of whether or not time machines are forbidden by the laws of physics, he will write an article for the public, explaining.”
With this chapter of this book, I am making good on that promise.
Chronology Protection?
I n February 1989, as the hoopla in the press was beginning to subside, and while Echeverria, Klinkhammer, and I were struggling with Polchinski’s paradox, I flew to Bozeman, Montana, to give a lecture. There I ran into Bill Hiscock, a former student of Charles Misner’s. As I have with so many colleagues, I pressed Hiscock for his views on wormholes and time machines. I was searching for cogent criticisms, new ideas, new viewpoints.
“Maybe you should study electromagnetic vacuum fluctuations,” Hiscock told me. “Maybe they will destroy the wormhole when infinitely advanced beings try to turn it into a time machine.” Hiscock had in mind the thought experiment in which my wife Carolee (assumed to be infinitely advanced) is flying back to Earth in the family spacecraft with one wormhole mouth, while I sit on Earth with the other mouth, and the wormhole is on the verge of becoming a time machine (Figures 14.7 and 14.8 above). Hiscock was speculating that electromagnetic vacuum fluctuations might circulate through the wormhole in the same manner as did bits of radiation in Figure 14.8; and, piling up on themselves, the fluctuations might become infinitely violent and destroy the wormhole.
I was skeptical. A year earlier, on my drive home from Chicago, I had convinced myself that bits of radiation, circulating through the wormhole, will not pile up on themselves, create an infinitely energetic beam, and destroy the wormhole. By defocusing the radiation, the wormhole saves itself. Surely, I thought, the wormhole will also defocus a circulating beam of electromagnetic vacuum fluctuations and thereby save itself.
On the other hand, I thought to myself, time machines are such a radical concept in physics that we must investigate anything which has any chance at all of destroying them. So, despite my skepticism, I set out with a postdoc in my group, Sung-Won Kim, to compute the behavior of circulating vacuum fluctuations.
Though we were helped greatly by mathematical tools and ideas that Hiscock and Deborah Konkowski had developed a few years earlier, Kim and I were hampered by our own ineptness. Neither of us was an expert on the laws that govern the circulating vacuum fluctuations: the laws of quantum fields in curved spacetime (Chapter 13 ). Finally, however, in February 1990, after a full year of false starts and mistakes, our calculations coalesced and gave an answer.
I was surprised and shocked. Despite the wormhole’s attempt to defocus them, the vacuum fluctuations tended to refocus of their own accord (Figure 14.11). Defocused by the wormhole, they splayed out from the mouth on Earth as though they were going to miss the spacecraft; then of their own accord, as though being attracted by some mysterious force, they zeroed in on the wormhole mouth in Carolee’s spacecraft. Returning to Earth through the wormhole, they then splayed out from the mouth on Earth again, and zeroed in once again on the mouth in the spacecraft. Over and over again they repeated this motion, building up an intense beam of fluctuational energy.
Will this beam of electromagnetic vacuum fluctuations be intense enough to destroy the wormhole? Kim and I asked ourselves. For eight months, February to September 1990, we struggled with this question. Finally, after several flip-flops, we concluded (incorrectly) “probably not.” Our reasoning seemed compelling to us and to the several colleagues we ran it past, so we laid it out in a manuscript and submitted it to the Physical Review.
Our reasoning was this: Our calculations had shown that the circulating electromagnetic vacuum fluctuations are infinitely intense only for a vanishingly short period of time. They rise to their peak at precisely the instant when it is first possible to use the wormhole for backward time travel (that is, at the moment when the wormhole first becomes a time machine), and then they immediately start to die out; see Figure 14.12.
Now, the (ill-understood) laws of quantum gravity seem to insist that there is no such thing as a “vanishingly short period of time.” Rather, just as fluctuations of spacetime curvature make the concept of length meaningless on scales smaller than the Planck–Wheeler length, 10 −33 centimeter (Figure 14.3 and associated discussion), so also the curvature fluctuations should make the concept of time meaningless on scales smaller than 10 −43 second (the “Planck-Wheeler time,” which is equal to the Planck–Wheeler length divided by the speed of light). Time intervals shorter than this cannot exist, the laws of quantum gravity seem to insist. The concepts of before and after and evolution with time make no sense during intervals so small.

14.11 As Carolee and I try to convert a wormhole into a time machine by the method of Figure 14.7, electromagnetic vacuum fluctuations zoom between the two mouths and through the wormhole, piling up on themselves and creating a beam of huge fluctuational energy.
Therefore, Kim and I reasoned, the circulating electromagnetic vacuum fluctuations must stop evolving with time, that is, must stop growing, 10 −43 second before the wormhole becomes a time machine; the laws of quantum gravity must cut off the fluctuations’ growth. And the quantum gravity laws will let the fluctuations continue their evolution again only 10 −43 second after the time machine is born, which means after they have begun to die out. In between these times, there is no time and there is no evolution (Figure 14.12). The crucial issue, then, was just how intense has the beam of circulating fluctuations become when quantum gravity cuts off their growth? Our calculations were clear and unequivocal: The beam, when it stops growing, is far too weak to damage the wormhole, and therefore, in the words of our manuscript, it seemed likely that “vacuum fluctuations cannot prevent the formation of or existence of closed time-like curves.” (Closed time-like curves is physicists’ jargon for “time machines”; having been burned by the press, I had stopped using the phrase “time machines” in my papers; and the press, unfamiliar with physicists’ jargon, was now unaware of the new time machine results I was publishing.)
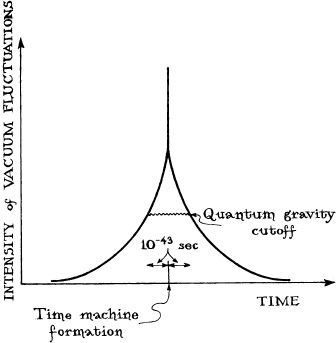
14.12 Evolution of the intensity of the electromagnetic vacuum fluctuations that circulate through a wormhole just before and just after the wormhole becomes a time machine.
I n September 1990, when we submitted our manuscript to the Physical Review, Kim and I sent copies to a number of colleagues, including Stephen Hawking. Hawking read our manuscript with interest—and disagreed. Hawking had no quarrel with our calculation of the beam of circulating vacuum fluctuations (and, in fact, a similar calculation by Valery Frolov in Moscow had by then verified our results). Hawking’s quarrel was with our analysis of quantum gravity’s effects.
Hawking agreed that quantum gravity was likely to cut off the growth of the vacuum fluctuations 10 −43 second before the time machine is created, that is, 10 −43 second before they otherwise would become infinitely strong. “But 10 −43 second as measured by whom? In whose reference frame?” he asked. Time is “relative,” not absolute, Hawking reminded us; it depends on one’s reference frame. Kim and I had assumed that the appropriate reference frame was that of somebody at rest in the wormhole throat. Hawking argued, instead (in effect), for a different choice of reference frame: that of the fluctuations themselves—or, stated more precisely, the reference frame of an observer who circulates, along with the fluctuations, from Earth to spacecraft and through the wormhole so rapidly that he sees the Earth—spacecraft distance contracted from 10 light-years (10 19 centimeters) down to the Planck—Wheeler length (10 −33 centimeter). The laws of quantum gravity can take over and stop the growth of the beam only 10 −43 second before the wormhole becomes a time machine, as seen by such a circulating observer, Hawking conjectured.
Translating back to the viewpoint of an observer at rest in the wormhole (the observer that Kim and I had relied on), Hawking’s conjecture meant that the quantum gravity cutoff occurs 10 −95 second before the wormhole becomes a time machine, not 10 −43 second—and by then, according to our calculations, the vacuum fluctuational beam is strong enough, but just barely so, that it might indeed destroy the wormhole.
H awking’s conjecture about the location of the quantum gravity cutoff was cogent. He might well be right, Kim and I concluded after much contemplation; and we managed to change our paper to say so before it got published.
The bottom line, however, was equivocal. Even if Hawking was right, it was far from clear whether the beam of vacuum fluctuations would destroy the wormhole or not—and to find out for certain would require understanding what quantum gravity does, when it takes hold in the 10 −95 -second interval around the moment of time machine formation.
To put it succinctly, the laws if quantum gravity are hiding from us the answer to whether wormholes can be converted successfully into time machines. To learn the answer, we humans must first become experts on quantum gravity’s laws.
Hawking has a firm opinion on time machines. He thinks that nature abhors them, and he has embodied that abhorence in a conjecture, the chronology protection conjecture, which says that the laws if physics do not allow time machines. (Hawking, in his characteristic off-the-wall humor, describes this as a conjecture that will “keep the world safe for historians.”)
Hawking suspects that the growing beam of vacuum fluctuations is nature’s way of enforcing chronology protection: Whenever one tries to make a time machine, and no matter what kind of device one uses in one’s attempt (a wormhole, a spinning cylinder, 13 a “cosmic string” 14 or whatever), just before one ’s device becomes a time machine, a beam of vacuum fluctuations will circulate through the device and destroy it Hawking seems ready to bet heavily on this outcome.
I am not willing to take the other side in such a bet. I do enjoy making bets with Hawking, but only bets that I have a reasonable chance of winning. My strong gut feeling is that I would lose this one. My own calculations with Kim, and unpublished calculations that Eanna Flanagan (a student of mine) has done more recently, suggest to me that Hawking is likely to be right. Every time machine is likely to self destruct (by means of circulating vacuum fluctuations) at the moment one tries to activate it. However, we cannot know for sure until physicists have fathomed in depth the laws of quantum gravity.
1. I have chosen to write this chapter solely from my own personal viewpoint. It therefore is much less objective than the rest of the book, and represents other people’s research much less fairly and less completely than it does my own.
2. See the “Best Guesses” section of Chapter 13 .
3. In technical language, we say that the exotic material “violates the averaged weak energy condition.”
4. See especially pages 347 , 348 , and 406 of Contact by Carl Sagan. There the exotic condition (negative average energy density as seen by light beams traveling through the wormhole) is expressed in a different, but equivalent way: As seen by someone at rest inside the wormhole, the material must have a large tension, along the radial direction, a tension that is bigger than the material’s energy density.
5. Chapter 13 .
6.
The Planck–Wheeler length is the square root of the Planck–Wheeler area (which entered into the formula for the entropy of a black hole,
Chapter 12
); it is given by the formula
![]() , where
G
= 6.670 × 10
−8
dyne-centimeter
2
/gram
2
is Newton’s gravitation constant, ħ= 1.055 × 10
−27
erg-second is Planck’s quantum mechanical constant, and
c
= 2.998 × 10
10
centimeter/second is the speed of light.
, where
G
= 6.670 × 10
−8
dyne-centimeter
2
/gram
2
is Newton’s gravitation constant, ħ= 1.055 × 10
−27
erg-second is Planck’s quantum mechanical constant, and
c
= 2.998 × 10
10
centimeter/second is the speed of light.
7. I wish that I could draw a simple, clear picture to show how this smooth creation of a wormhole is accomplished; unfortunately, I cannot.
8. This time machine and others described later in this chapter are by no means the first time machine—type solutions to the Einstein field equation that people have found. In 1937, W. J. van Stockum in Edinburgh discovered a solution in which an infinitely long, rapidly spinning cylinder functions as a time machine. Physicists have long objected that nothing in the Universe can be infinitely long, and they have suspected (but nobody has proved) that, if the length of the cylinder were made finite, it would cease to be a time machine. In 1949, Kurt Godel, at the Institute for Advanced Study in Princeton, New Jersey, found a solution to Einstein’s equation that describes a whole universe which spins but does not expand or contract, and in which one can travel backward in time by simply going out to great distances from Earth and then returning. Physicists object, of course, that our real Universe does not at all resemble Godel’s solution: It is not spinning, at least not much, and it is expanding. In 1976 Frank Tipler used the Einstein field equation to prove that, in order to create a time machine in a finite-sized region of space, one must use exotic material as part of the machine. (Since any traversable wormhole must be threaded by exotic material, the wormhole-based time machines described in this chapter satisfy Tipler’s requirement.)
9. In reality, if Carolee were to accelerate up to the speed of light and then back down so quickly, the acceleration would be so great that it would kill her and mutilate her body. However, in the spirit of a physicist’s thought experiment, I shall pretend that her body is made of such strong stuff that she can survive the acceleration comfortably.
10. In most science fiction literature, the term “grandfather paradox” is used rather than “matricide paradox.” Presumably, the chivalrous men who dominate the science fiction writing profession feel more comfortable pushing the murder back a generation and onto a male.
11. I and my four siblings are very respectful and obedient toward our mother; see, for example, Footnote 2 in Chapter 7 . Accordingly, I have sought and received permission from my mother to use this example.
12. Three years later, John Friedman and Mike Morris together managed to prove rigorously that, when waves travel backward in time through a wormhole, there indeed are no unresolvable paradoxes—provided the waves superimpose linearly on themselves in the manner of Box 10.3.
13. See Footnote 8 on page 499 .
14. Recently Richard Gott of Princeton University has discovered that one can make a time machine by taking two infinitely long cosmic strings (hypothetical objects that might or might not exist in the real Universe) and moving them past each other at very high speed.
![]()
an overview of Einstein’s legacy,
past and future,
and an update on several central characters
I t now is nearly a full century since Einstein destroyed Newton’s concept of space and time as absolute, and began laying the foundations for his own legacy. Over the intervening century, Einstein’s legacy has grown to include, among many other things, a warpage of spacetime and a set of exotic objects made wholly and solely from that warpage: black holes, gravitational waves, singularities (clothed and naked), wormholes, and time machines.
At one epoch in history or another, physicists have regarded each of these objects as outrageous.
• We have met, in this book, Eddington’s, Wheeler’s, and even Einstein’s vigorous skepticism about black holes; Eddington and Einstein died before they were firmly proved wrong, but Wheeler became a convert and black-hole advocate.
• During the 1940s and 1950s, a number of physicists, building on mistaken interpretations of the general relativistic mathematics they were studying, were highly skeptical of gravitational waves (ripples of curvature)—but that is a story for another book, and the skepticism long since has vanished.
• It was a horrendous shock to most physicists, and still is to many, to discover that singularities are an inevitable consequence of Einstein’s general relativistic laws. Some physicists derive comfort from faith in Penrose’s cosmic censorship conjecture (that all singularities are clothed; naked singularities are forbidden). But whether cosmic censorship is wrong or right, most physicists have accommodated to singularities and, like Wheeler, expect the ill-understood laws of quantum gravity to tame them—ruling and controlling them in just the same way as Newton’s or Einstein’s laws of gravity rule the planets and control their orbits around the Sun.
• Wormholes and time machines today are regarded as outrageous by most physicists, even though Einstein’s general relativistic laws permit them to exist. Skeptical physicists can take comfort, however, in our newfound knowledge that the existence of wormholes and time machines is controlled not by Einstein’s rather permissive laws, but rather by the more restrictive laws of quantum fields in curved spacetime, and quantum gravity. When we understand those laws better, perhaps they will teach us unequivocally that physical laws always protect the Universe against wormholes and time machines—or at least time machines. Perhaps.
W hat can we expect in the coming century, the second century of Einstein’s legacy?
It seems likely that the revolution in our understanding of space, time, and objects built from spacetime warpage will be no less than in the first century. The seeds for revolution have been laid:
• Gravitational-wave detectors will soon bring us observational maps of black holes, and the symphonic sounds of black holes colliding—symphonies filled with rich, new information about how warped spacetime behaves when wildly vibrating. Supercomputer simulations will attempt to replicate the symphonies and tell us what they mean, and black holes thereby will become objects of detailed experimental scrutiny. What will that scrutiny teach us? There will be surprises.
• Ultimately, in the coming century, most likely sooner rather than later, some insightful physicist will discover and unveil the laws of quantum gravity, in all their intimate detail.
• With those quantum gravity laws in hand, we may figure out precisely how our Universe’s spacetime came into being, how it emerged from the quantum foam and froth of the big bang singularity. We may learn for sure the meaning or the meaninglessness of the oft-asked question, “What preceded the big bang?” We may learn for sure whether quantum foam produces multiple universes with ease, and the full details of how spacetime gets destroyed in the singularity at the core of a black hole or in the big crunch, and how and whether and where spacetime gets re-created again. And we may learn whether the laws of quantum gravity permit or forbid time machines: Must time machines always self-destruct at the moment they are activated?
• The laws of quantum gravity are not the final set of physical laws along the route that has led from Newton to special relativity, to general relativity and quantum theory, and then to quantum gravity. The quantum gravity laws will still have to be married to (unified with) the laws that govern nature’s other fundamental forces: the electromagnetic force, the weak force, and the strong force. We will probably learn the details of that unification in the coming century—and again, most likely sooner rather than later; and that unification may radically alter our view of the Universe. And what then? No human today can foresee beyond that point, I believe—and yet, that point may well come in my own lifetime, and in yours.
In Closing, November 1993
Albert Einstein spent most of his last twenty-five years in a fruitless quest to unify his general relativistic laws of physics with Maxwell’s laws of electromagnetism; he did not know that the most important unification is with quantum mechanics. He died in Princeton, New Jersey, in 1955 at the age of seventy-six.
Subrahmanyan Chandrasekhar, now eighty-three years old, continues to plumb the secrets of Einstein’s field equation, often in collaboration with much younger colleagues. In recent years he has taught us much about pulsations of stars and collisions of gravitational waves.
Fritz Zwicky became less a theorist and more an observational astronomer as he aged; and he continued to generate controversial, prescient ideas, though not on the topics of this book. He retired from his Caltech professorship in 1968 and moved to Switzerland, where he spent his final years promoting his own inside track to knowledge: the “morphological method.” He died in 1974.
Lev Davidovich Landau recovered intellectually, but not emotionally, from his year in prison (1938–39) and then continued on as the dominant figure and most revered teacher among Soviet theoretical physicists. In 1962 he was critically injured in an automobile accident, which left him with brain damage that changed his personality and destroyed his ability to do physics. He died in 1968, but his closest friends said of him afterward, “For me, ‘Dau died in 1962.”
Yakov Borisovich Zel’dovich remained the world’s most influential astrophysicist through the 1970s and into the 1980s. However, in 1978, in a tragic interpersonal explosion, he split off from most of his research group (the most powerful team of theoretical astrophysicists that the world has ever seen). He tried to rebuild with a fresh set of young colleagues, but was only partially successful, and then in the 1980s he became a guru for astrophysicists and cosmologists, worldwide. He died of a heart attack in Moscow in 1987, soon after Gorbachev’s political changes made it possible for him to travel to America for the first time.
Igor Dmitrievich Novikov became the leader of the Zel’dovich/ Novikov research group after the split with Zel’dovich. Through the 1980s he held the group together with the same kind of fire and stimulus as Zel’dovich had mustered in the old days. However, without Zel’dovich, his group was merely among the best in the world, and not far ahead of everyone else, as before. With the collapse of the Soviet Union in 1991, and following a heart operation that made him feel his finiteness, Novikov moved to the University of Copenhagen in Denmark, where he is now creating a new Theoretical Astrophysics Center.
Vitaly Lazarevich Ginzburg, at age seventy-seven, continues to do forefront research in several different branches of physics and astrophysics. During Andrei Sakharov’s exile to Gorky in 1980–86, Ginzburg, as Sakharov’s official “boss” at the Lebedev Institute in Moscow, refused to fire him and acted as a sort of protector. Under Gorbachev’s perestroika, Ginzburg and Sakharov were both elected members of the Chamber of People’s Deputies of the U.S.S.R., where they pushed for reform. Sakharov died of a heart attack in 1989.
J. Robert Oppenheimer, though repudiated by the United States government in his 1954 security clearance hearings, became a hero to the majority of the physics community. He never returned to research, but he remained closely in touch with most all branches of physics, and served as a powerful foil off whom younger physicists could bounce their ideas, until his death from cancer in 1967.
John Wheeler, at age eighty-two, continues his quest to understand the marriage of quantum mechanics and general relativity—and continues to inspire younger generations with his lectures and writings, most notably his recent book A Journey into Gravity and Spacetime (Wheeler, 1990).
Roger Penrose, like Wheeler and many others, is obsessed with the marriage of general relativity and quantum mechanics and with the ill-understood laws of quantum gravity that should spring forth from that marriage. He has written about his unconventional ideas in a book for nonphysicists (The Emperor’s New Mind, Penrose, 1989). Many physicists are skeptical of his views, but Penrose has been right so many times before . . .
Stephen Hawking also continues to be obsessed with the laws of quantum gravity, and most especially with the question of what those laws predict about the origin of the Universe. Like Penrose, he has written a book for nonphysicists, describing his ideas (A Brief History of Time, Hawking, 1988). His health holds strong, despite his ALS
![]()
my debts of gratitude
to friends and colleagues
who influenced this book
E laine Hawkes Watson, by her boundless curiosity about the Universe, inspired me to embark on this book. During my fifteen years of on-and-off writing, I received invaluable encouragement and support from several close friends and family: Linda Thorne, Kares Thorne, Bret Thorne, Alison Thorne, Estelle Gregory, Bonnie Schumaker, and most especially my wife, Carolee Winstein.
I am indebted to a number of my physicist, astrophysicist, and astronomer colleagues, who consented to be interviewed by me on tape about their recollections of the historical events and research efforts described in this book. Their names appear in the list of taped interviews at the beginning of the bibliography.
Four of my colleagues, Vladimir Braginsky, Stephen Hawking. Werner Israel, and Carl Sagan, were kind enough to read the entire manuscript and give me detailed critiques. Many others read individual chapters or several chapters and straightened me out on important historical and scientific details: Vladimir Belinsky, Roger Blandford, Carlton Caves, S. Chandrasekhar, Ronald Drever, Vitaly Ginzburg, Jesse Greenstein, Isaac Khalatnikov, Igor Novikov, Roger Penrose, Dennis Sciama, Robert Serber, Robert Spero, Alexi Starobinsky, Rochus Vogt, Robert Wald, John Wheeler, and Yakov Borisovich Zel’dovich. Without the advice of these colleagues, the book would be far less accurate than it is. However, one should not assume that my colleagues agree with me or approve of all my interpretations of our joint history. Inevitably there have been a few conflicts of viewpoint. In the text, for pedagogy’s sake, I hew to my own viewpoint (often, but not always, significantly influenced by my colleagues’ critiques). In the notes, for historical accuracy, I expose some of the conflicts.
Lynda Obst tore much of the first version of the book to shreds. I thank her. K. C. Cole tore the second version to shreds and then patiently gave me crucial advice on draft after draft, until the presentation was honed. To K. C. I am especially indebted. I also thank Debra Makay for meticulously cleaning up the final manuscript; she is even more of a perfectionist than 1.
The book was significantly improved by critiques from several nonphysicist readers: Ludmila (Lily) Birladeanu, Doris Driicker, Linda Feferman, Rebecca Lewth-waite, Peter Lyman, Deanna Metzger, Phil Richman, Barrie Thorne, Alison Thorne, and Carolee Winstein. I thank them, and I thank Helen Knudsen for locating a number of references and facts—some unbelievably obscure.
I was fortunate to run across Matthew Zimet’s delightful drawings in Heinz Pagel’s book The Cosmic Code, and attract him to illustrate my book as well. His illustrations add so much.
Finally, I wish to thank the Commonwealth Fund Book Program and especially Alexander G. Bearn and Antonina W. Bouis—and also Ed Barber of W.W. Norton and Company—for their support, their patience, and their faith in me as a writer during the years that it took to bring this book to completion.
![]()
a list of characters
who appear significantly
at several different places in the book
N OTE : The following descriptions are meant to serve solely as reminders of and cross-references to each person’s various appearances in this book. These descriptions are not intended as biographical sketches. (Most of these people have made major contributions to science that are not relevant to this book and therefore are not listed here.) The principal criterion for inclusion in this section is not importance of contributions, but rather multiple appearances of the person at several different locations in the book.
Baade, WaIter (1893–1960). German born, American optical astronomer; with Zwicky, developed the concept of a supernova and its connection to neutron stars ( Chapter 5 ); identified the galaxies associated with cosmic radio sources ( Chapter 9 ).
Bardeen, James Maxwell (b. 1939). American theoretical physicist; showed that many or most black holes in our Universe should be rapidly spinning and, with Petterson, predicted the influence of the holes’ spins on surrounding accretion disks (Chapter 9 ); with Carter and Hawking, discovered the four laws of black-hole mechanics (the laws of evolution of black holes) (Chapter 12 ).
Bekenstein, Jacob (b. 1947). Israeli theoretical physicist; student of Wheeler’s; with Hartle, showed that one cannot discern, by any external study of a black hole, what kinds of particles were among the material that formed it (Chapter 7 ); proposed that the surface area of a black hole is its entropy in disguise, and carried on a battle with Hawking over this idea, ultimately winning (Chapter 12 ).
Bohr, Niels Hendrik David (1885–1962). Danish theoretical physicist; Nobel laureate; one of the founders of quantum mechanics; mentor for many of the leading physicists of the middle twentieth century, including Lev Landau and John Wheeler; advised Chandrasekhar in his battle with Eddington (Chapter 4 ); tried to save Landau from prison (Chapter 5 ); with Wheeler developed the theory of nuclear fission (Chapter 6 ).
Braginsky, Vladimir Borisovich (b. 1931). Russian experimental physicist; discovered quantum mechanical limits on the precision of physical measurements, including those of gravitational-wave detectors (Chapter 10 ); inventor of the concept of “quantum nondemolition” devices, which circumvent those quantum limits (Chapter 10 ).
Carter, Brandon (b. 1942). Australian theoretical physicist; student of Dennis Sciama’s in Cambridge, England; later moved to France; elucidated the properties of spinning black holes (Chapter 7 ); with others, proved that a black hole has no hair (Chapter 7 ); with Bardeen and Hawking discovered the four laws of black-hole mechanics (the laws of evolution of black holes) (Chapter 1 2).
Chandrasekhar, Subrahmanyan (b. 1910). Indian born, American astrophysicist; Nobel laureate; proved that there is a maximum mass for white-dwarf stars and fought a battle with Eddington over the correctness of his prediction (Chapter 4 ); developed much of the theory of how black holes respond to small perturbations (Chapter 7 ).
Eddington, Arthur Stanley (1882–1944). British astrophysicist; leading early exponent of Einstein’s laws of general relativity (Chapter 3 ); vigorous opponent of the concept of a black hole and of Chandrasekhar’s conclusion that white dwarfs have a maximum mass (Chapters 3 and 4 ).
Einstein Albert (1879–1955). German born, Swiss/American theoretical physicist; Nobel laureate; formulated the laws of special relativity (Chapter 1 ) and general relativity (Chapter 2 ); showed that light is simultaneously a particle and a wave (Chapter 4 ); opposed the concept of a black hole (Chapter 3 ).
Geroch, Robert (b. 1942). American theoretical physicist; student of Wheeler’s; with others, developed global methods for analyzing black holes (Chapter 13 ); showed that the topology of space can change (for example, when a wormhole forms) only if a time machine is produced in the process (Chapter 14 ); with Wald, gave the first argument suggesting that time machines might be destroyed whenever they try to form (Chapter 14 ).
Giacconi, Riccardo (b. 1931). Italian born, American experimental physicist and astrophysicist; led the team that discovered the first X-ray star, in 1962, using a detector flown on a rocket (Chapter 8 ); led the team that designed and built the Uhuru X-ray satellite, which produced the first strong X-ray evidence that Cygnus X-1 is a black hole (Chapter 8 ).
Ginzburg, Vitaly Lazarevich (b. 1916). Soviet theoretical physicist; invented the LiD fuel for the Soviet hydrogen bomb and then was separated from the bomb project (Chapter 6 ); with Landau, developed an explanation for the origin of superconductivity (Chapters 6 and 9 ); discovered the first evidence that a black hole has no hair (Chapter 7 ); developed the synchrotron radiation explanation for the origin of cosmic radio waves (Chapter 9 ).
Greenstein, Jesse L. (b. 1909). American optical astronomer; colleague of Zwicky’s (Chapter 5 ); with Fred Whipple found it impossible to explain cosmic radio waves (Chapter 9 ); triggered the beginning of America’s research effort in radio astronomy (Chapter 9 ); with Maarten Schmidt, discovered quasars (Chapter 9 ).
Hartle, James B. (b. 1939). Student of Wheeler’s; with Bekenstein, showed that one cannot discern, by any external study of a black hole, what kinds of particles were among the material that formed it (Chapter 7 ); with Hawking, discovered the laws that govern the evolution of a black hole’s horizon (Chapter 12 ); with Hawking, is developing insights into the laws of quantum gravity (Chapter 13 ).
Hawking, Stephen W. (b. 1942). British theoretical physicist; student of Sciama’s; developed key parts of the proof that a black hole has no hair (Chapter 7 ); with Bardeen and Carter, discovered the four laws of black-hole mechanics (the laws of evolution of black holes) (Chapter 12 ); discovered that, if one ignores the laws of quantum mechanics, the surface areas of black holes can only increase, but quantum mechanics makes black holes evaporate and shrink (Chapter 12 ); showed that tiny black holes could have formed in the big bang and, with Page, placed observational limits on such primordial holes based on astronomers not seeing gamma rays produced by their evaporation (Chapter 12 ); developed global (topological) methods for analyzing black holes (Chapter 13 ); with Penrose, proved that the big bang contained a singularity (Chapter 13 ); formulated the chronology protection conjecture and argued that it is enforced by vacuum fluctuations destroying any time machine at the moment it is created (Chapter 14 ); made bets with Kip Thorne over whether Cygnus X-1 is a black hole (Chapter 8 ) and whether naked singularities can form in our Universe (Chapter 13 ).
Israel, Werner (b. 1931). South African born, Canadian theoretical physicist; proved that every nonspinning black hole must be spherical, and gave evidence that a black hole loses its “hair” by radiating it away (Chapter 7 ); discovered that the surface areas of black holes can only increase, but did not realize the significance of this conclusion (Chapter 12 ); with Poisson and Ori, showed that the tidal forces that surround a black hole’s singularity become weaker as the hole ages (Chapter 13 ); developed insights into the early history of black-hole research (Chapter 3 ).
Kerr, Roy P. (b. 1934). New Zealander mathematician; discovered the solution to Einstein’s field equation, which describes a spinning black hole: the “Kerr solution” (Chapter 7 ).
Landau, Lev Davidovich (1908–1968). Soviet theoretical physicist; Nobel laureate; transfused theoretical physics from Western Europe into the U.S.S.R. in the 1930s (Chapters 5 and 13 ); tried to explain stellar heat as produced by stellar material being captured onto a neutron core at the star’s center, and thereby triggered Oppenheimer’s research on neutron stars and black holes (Chapter 5 ); was imprisoned in Stalin’s Great Terror and then released so he could develop the theory of superfluidity (Chapter 5 ); contributed to Soviet nuclear weapons research (Chapter 6 ).
Laplace, Pierre Simon (1749–1827). French natural philosopher; developed and popularized the concept of a dark star (black hole) as governed by Newton’s laws of physics (Chapters 3 and 6 ).
Lorentz, Hendrik Antoon (1853–1928). Dutch theoretical physicist; Nobel laureate; developed key foundations for the laws of special relativity, the most important being the Lorentz–Fitzgerald contraction and time dilation (Chapter 1 ); friend and associate of Einstein when Einstein was developing his general relativistic laws of physics (Chapter 2 ).
Maxwell, James Clerk (1831–1879). British theoretical physicist; developed the laws of electricity and magnetism (Chapter 1 ).
Michell, John (1724–1793). British natural philosopher; developed and popularized the concept of a dark star (black hole) as governed by Newton’s laws of physics (Chapters 3 and 6 ).
Michelson, Albert Abraham (1852–1931). German-born, American experimental physicist; Nobel laureate; invented the techniques of interferometry (Chapter 1 ); used those techniques to discover that the speed of light is independent of one’s velocity through the Universe (Chapter 1 ).
Minkowski, Hermann (1864–1909). German theoretical physicist; teacher of Einstein (Chapter 1 ); discovered that space and time are unified into spacetime (Chapter 2 ).
Misner, Charles W. (b. 1932). American theoretical physicist; student of Wheeler’s; developed an insightful embedding diagram description of how an imploding star produces a black hole (Chapter 6 ); created a research group that contributed significantly to the “golden age” of black-hole research (Chapter 7 ); discovered that electromagnetic and other waves propagating near a spinning black hole can extract rotational energy from the hole and use it to amplify themselves (Chapter 12 ); discovered the oscillatory, “mixmaster” oscillations of tidal gravity near singularities (Chapter 13 ).
Newton, Isaac (1642–1727). British natural philosopher; developed the foundations for the Newtonian laws of physics and for the concept of space and time as absolute (Chapter 1 ); developed the Newtonian laws of gravity (Chapter 2 ).
Novikov, Igor Dmitrievich (b. 1935). Soviet theoretical physicist and astrophysicist; student of Zel’dovich’s; with Doroshkevich and Zel’dovich, developed some of the key initial evidence that a black hole has no hair (Chapter 7 ); with Zel’dovich, proposed the method for astronomical searches for black holes in our galaxy that seems to have finally succeeded (Chapter 8 ); with Thorne, developed the theory of the structures of accretion disks around black holes (Chapter 12 ); with Doroshkevich, predicted that the tidal forces inside a black hole must change as the hole ages (Chapter 13 ); carried out research on whether the laws of physics permit time machines (Chapter 14 ).
Oppenheimer, J. Robert (1904–1967). American theoretical physicist; transfused theoretical physics from Western Europe to the United States in the 1930s (Chapter 5 ); with Serber, disproved Landau’s claim that stars might be kept hot by neutron cores, and with Volkoff, demonstrated that there is a maximum possible mass for neutron stars (Chapter 5 ); with Snyder, demonstrated, in a highly idealized model, that when massive stars die, they must implode to form black holes, and elucidated key features of the implosion (Chapter 6 ); led the American atomic bomb project, opposed the hydrogen bomb project early on and then endorsed it and lost his security clearance (Chapter 6 ); did battle with Wheeler over whether implosion produces black holes (Chapter 6 ).
Penrose, Roger (b. 1931). British mathematician and theoretical physicist; protege of Sciama’s; speculated that black holes lose their hair by radiating it away (Chapter 7 ); discovered that spinning black holes store huge amounts of energy in the swirl of space outside their horizons and that this energy can be extracted (Chapter 7 ); developed the concept of a black hole’s apparent horizon (Chapters 12 and 13 ); discovered that the surface areas of black holes must increase, but did not realize the significance of that conclusion (Chapter 12 ); invented and developed global (topological) methods for analyzing black holes (Chapter 13 ); proved that black holes must have singularities in their cores and, with Hawking, proved that the big bang contained a singularity (Chapter 13 ); proposed the cosmic censorship conjecture, that the laws of physics prevent naked singularities from forming in our Universe (Chapter 13 ).
Press, William H. (b. 1948). American theoretical physicist and astrophysicist; student of Thorne’s; with Teukolsky, proved that black holes are stable against small perturbations (Chapters 7 and 12 ); discovered that black holes can pulsate (Chapter 7 ); organized the funeral for the golden age of black-hole research (Chapter 7 ).
Price, Richard H. (b. 1943). American theoretical physicist and astrophysicist; student of Thorne’s; gave the definitive proof that a black hole loses its hair by radiating the hair away and proved that anything which can be radiated will be radiated away completely (Chapter 7 ); saw evidence that black holes pulsate but did not recognize its significance (Chapter 7 ); with others developed the membrane paradigm for black holes (Chapter 11 ); worried about Thorne’s sanity when Thorne initiated research on time machines (Chapter 14 ).
Rees, Martin (b. 1942). British astrophysicist; student of Sciama’s; developed models that explain the observed features of binary systems in which a black hole accretes gas from a companion star (Chapter 8 ); proposed that the giant lobes of a radio galaxy are powered by beams of energy that travel from the galaxy’s core to the lobes, and with Blandford developed detailed models for the beams (Chapter 9 ); with Blandford and others, developed models that explain how a supermassive black hole can energize radio galaxies, quasars, and active galactic nuclei (Chapter 9 ).
Sakharov, Andrei Dmitrievich (1921–1989). Soviet theoretical physicist; invented key ideas that underlie the Soviet hydrogen bomb (Chapter 6 ); close friend, associate, and competitor of Zel’dovich’s (Chapters 6 and 7 ); later became the leading Soviet dissident and, after glasnost, Soviet saint.
Schwarzschild, Karl (1876–1916). German astrophysicist; discovered the Schwarzschild solution of the Einstein field equation, which describes the spacetime geometry of a nonspinning star that is either static or imploding, and also describes a nonspinning black hole (Chapter 3 ); discovered the solution of the Einstein equation for the interior of a constant-density star—a solution that Einstein used to argue that black holes cannot exist (Chapter 3 ).
Sciama, Dennis (b. 1926). British astrophysicist and mentor for British researchers on black holes (Chapters 7 and 13 ).
Tenkolsky, Sanl A. (b. 1947). South African born, American theoretical physicist; student of Thorne’s; invented and developed the formalism by which perturbations of spinning black holes are analyzed and, with Press, used his formalism to show that black holes are stable against small perturbations (Chapters 7 and 12 ); with Shapiro, discovered evidence that the laws of physics might permit naked singularities to form in our Universe (Chapter 13 ).
Thorne, Kip S. (b. 1940). American theoretical physicist; student of Wheeler’s; proposed the hoop conjecture which describes when black holes can form in an imploding star, and developed evidence for it (Chapter 7 ); made estimates of the gravitational waves from astrophysical sources and contributed to ideas and plans for the detection of those waves (Chapter 10 ); with others, developed the membrane paradigm for black holes (Chapter 11 ); developed ideas about the statistical origin of the entropy of a black hole (Chapter 12 ); probed the laws of physics by means of thought experiments about wormholes and time machines (Chapter 14 ).
Wald, Robert M. (b. 1947). American theoretical physicist; student of Wheeler’s; contributed to the Teukolsky formalism for analyzing perturbations of black holes and its applications (Chapter 7 ); with others, developed an understanding of how electric fields behave outside a black hole—an understanding that underlies the membrane paradigm (Chapter 11 ); contributed to the theory of the evaporation of black holes and its implications for the origin of black-hole entropy (Chapter 12 ); with Geroch, gave the first argument suggesting that time machines might be destroyed whenever they try to form (Chapter 14 ).
Weber, Joseph (b. 1919). American experimental physicist; invented the world’s first gravitational-wave detectors (“bar detectors”) and co-invented interferometric detectors for gravitational waves (Chapter 10 ); universally regarded as the “father” of the field of gravitational-wave detection.
Wheeler, John Archibald (b. 1911). American theoretical physicist; mentor for American researchers on black holes and other aspects of general relativity (Chapters 7); with Harrison and Wakano, developed the equation of state for cold, dead matter and a complete catalog of cold, dead stars, thereby firming up evidence that when massive stars die they must form black holes (Chapter 5 ); with Niels Bohr, developed the theory of nuclear fission (Chapter 6 ); led a team that designed the first American hydrogen bombs (Chapter 6 ); argued in a battle with Oppenheimer that black holes cannot form, then retracted the argument and became the leading proponent of black holes (Chapter 6 ); coined the phrases “black hole” (Chapter 6 ) and “a black hole has no hair” (Chapter 7 ); argued that the “issue of the final state” of gravitationally imploding stars is a key to understanding the marriage between general relativity and quantum mechanics, and in this argument anticipated Hawking’s discovery that black holes can evaporate (Chapters 6 and 13 ); developed foundations for the laws of quantum gravity and, most important, conceived and developed the concept of quantum foam, which we now suspect is the stuff of which singularities are made (Chapter 13 ); developed the concept of the Planck—Wheeler length and area (Chapters 12, 13, 14).
Zel’dovich, Yakov Borisovich (1914–1987). Soviet theoretical physicist and astrophysicist; mentor for Soviet astrophysicists (Chapter 7 ); developed the theory of nuclear chain reactions (Chapter 5 ); invented key ideas that underlie Soviet atomic and hydrogen bombs, and led a bomb design team (Chapter 6 ); with Doroshkevich and Novikov, developed early evidence that a black hole has no hair (Chapter 7 ); invented several methods for astronomical searches for black holes, one of which seems ultimately to have succeeded (Chapter 8 ); independently of Salpeter, proposed that supermassive black holes power quasars and radio galaxies (Chapter 9 ); conceived of the idea that the laws of quantum mechanics might cause spinning black holes to radiate and thereby lose their spin and, with Starobinsky, proved so, but then resisted Hawking’s proof that even nonspinning holes can radiate and evaporate (Chapter 12 ).
Zwicky, Fritz (1898–1974). Swiss-born American theoretical physicist, astrophysicist, and optical astronomer; with Baade, identified supernovae as a class of astronomical objects and proposed that they are powered by energy released when a normal star becomes a neutron star (Chapter 5 ).