![]()
in which black holes are found
to spin and pulsate,
store energy and release it,
and have no hair
T he year was 1975; the place, the University of Chicago on the south side of the city, near the shore of Lake Michigan. There, in a corner office overlooking 56th Street, Subrahmanyan Chandrasekhar was immersed in developing a full mathematical description of black holes. The black holes he was analyzing were radically different beasts from those of the early 1960s, when physicists had begun to embrace the concept of a black hole. The intervening decade had been a golden age of black-hole research, an era that revolutionized our understanding of general relativity’s predictions.
In 1964, at the beginning of the golden age, black holes were thought to be just what their name suggests: holes in space, down which things can fall, out of which nothing can emerge. But during the golden age, one calculation after another, by more than a hundred physicists using Einstein’s general relativity equations, had changed that picture. Now, as Chandrasekhar sat in his Chicago office, calculating, black holes were regarded not as mere quiescent holes in space, but rather as dynamical objects: A black hole should be able to spin, and as it spins it should create a tornado-like swirling motion in the curved spacetime around itself. Stored in that swirl should be enormous energies, energies that nature might tap and use to power cosmic explosions. When stars or planets or smaller holes fall into a big hole, they should set the big hole pulsating. The horizon of the big hole should pulsate in and out, just as the surface of the Earth pulsates up and down after an earthquake, and those pulsations should produce gravitational waves—ripples in the curvature of spacetime that propagate out through the Universe, carrying a symphonic description of the hole.
Perhaps the greatest surprise to emerge from the golden age was general relativity’s insistence that all the properties of a black hole are precisely predictable from just three numbers: the hole’s mass, its rate of spin, and its electric charge. From those three numbers, if one is sufficiently clever at mathematics, one should be able to compute, for example, the shape of the hole’s horizon, the strength of its gravitational pull, the details of the swirl of spacetime around it, and its frequencies of pulsation. Many of these properties were known by 1975, but not all. To compute and thereby learn all the remaining black-hole properties was a difficult challenge, precisely the kind of challenge that Chandrasekhar loved. He took it up, in 1975, as his personal quest.
For nearly forty years, the pain of his 1930s battles with Eddington had smoldered inside Chandrasekhar, impeding him from a return to research on the black-hole fates of massive stars. In those forty years he had laid many of the foundations for modern astrophysics—foundations for the theories of stars and their pulsations, of galaxies, of interstellar gas clouds, and much more. But throughout it all, the fascination of the fates of massive stars had attracted him. Finally, in the golden age, he had overcome his pain and returned.
He returned to a family of researchers who were almost all students and postdocs. The golden age was dominated by youth, and Chandrasekhar, young at heart but middle-aged and conservative in demeanor, was welcomed into their midst. On extended visits to Caltech and Cambridge, he could often be seen in cafeterias, surrounded by brightly and informally bedecked graduate students but himself attired in a conservative dark gray suit—”Chandrasekhar gray” his youthful friends called its color.
The golden age was brief. Caltech graduate student Bill Press had given the golden age its name, and in the summer of 1975, just as Chandrasekhar was embarking on his quest to compute the properties of black holes, Press organized its funeral: a four-day conference at Princeton University to which only researchers under the age of thirty were invited. 1 At the conference, Press and many of his young colleagues agreed that now was the time to move on to other research topics. The broad outlines of black holes as spinning, pulsating, dynamical objects were now in place, and the rapid pace of theoretical discoveries was beginning to slow. All that was left, it seemed, was to fill in the details. Chandrasekhar and a few others could do that handily, while his young (but now aging) friends sought new challenges elsewhere. Chandrasekhar was not pleased.

Top: Subrahmanyan Chandrasekhar at Caltech’s student cafeteria (“the Greasy”) with graduate students Saul Teukolsky (left) and Alan Lightman (right), in autumn 1971. BoUom: The participants in the conference/funeral for the golden age of black-hole research, Princeton University, summer 1975. Front row, left to right: Jacobus Petterson, Philip Yasskin, Bill Press, Larry Smarr, Beverly Berger, Georgia Witt, Bob Wald. Second and third rows, left to right: Philip Marcus, Peter D’Eath, Paul Schechter, Saul Teukolsky, Jim Nester, Paul Wiita, Michael Schull, Bernard Carr, Clifford Will, Tom Chester, Bill Unruh, Steve Christensen. [Top: courtesy Sándor J. Kovács; bottom: courtesy Saul Teukolsky.]

The Mentors: Wheeler, Zel’dovich, Sciama
W ho were these youths who revolutionized our understanding of black holes? Most of them were students, postdocs, and intellectual “grandchildren” of three remarkable master teachers: John Archibald Wheeler in Princeton, New Jersey, U.S.A.; Yakov Borisovich Zel’-dovich in Moscow, Russia, D.S.S.R.; and Dennis Sciama in Cambridge, England, U.K. Through their intellectual progeny, Wheeler, Zel’-dovich, and Sciama put their personal stamps on our modern understanding of black holes.
Each of these mentors had his own style. In fact, styles more different are hard to find. Wheeler was a charismatic, inspirational visionary. Zel’dovich was the hard-driving player/coach of a tightly knit team. Sciama was a self-sacrificing catalyst. We shall meet each of them in turn in the following pages.
H ow well I recall my first meeting with Wheeler. It was September 1962, two years before the advent of the golden age. Wheeler was a recent convert to the concept of a black hole, and I, at twenty-two years of age, had just graduated from Caltech and come to Princeton to pursue graduate study toward a Ph.D. My dream was to work on relativity research under Wheeler’s guidance, so I knocked on his office door that first time with trepidation.
Professor Wheeler greeted me with a warm smile, ushered me into his office, and began immediately (as though I were an esteemed colleague, not a total novice) to discuss the mysteries of stellar implosion. The mood and content of that stirring private discussion are captured in Wheeler’s writings of that era: “There have been few occasions in the history of physics when one could surmise more surely than one does now [in the study of stellar implosion] that he confronts a new phenomenon, with a mysterious nature of its own, waiting to be unravelled.... Whatever the outcome [of future studies], one feels that one has at last [in stellar implosion] a phenomenon where general relativity dramatically comes into its own, and where its fiery marriage with quantum physics will be consummated.” I emerged, an hour later, a convert.
Wheeler gave inspiration to an entourage of five to ten Princeton students and postdocs—inspiration, but not detailed guidance. He presumed that we were brilliant enough to develop the details for ourselves. To each of us he suggested a first research problem—some issue that might yield a bit of new insight about stellar implosion, or black holes, or the “fiery marriage” of general relativity with quantum physics. If that first problem turned out to be too hard, he would gently nudge us in some easier direction. If it turned out easy, he would prod us to extract from it all the insight we possibly could, then write a technical article on the insight, and then move on to a more challenging problem. We soon learned to keep several problems going at once—one problem so hard that it must be visited and revisited time after time over many months or years before it cracked, hopefully with a big payoff; and other problems much easier, with quicker payoffs. Through it all, Wheeler gave just barely enough advice to keep us from totally floundering, never so much that we felt he had solved our problem for us.
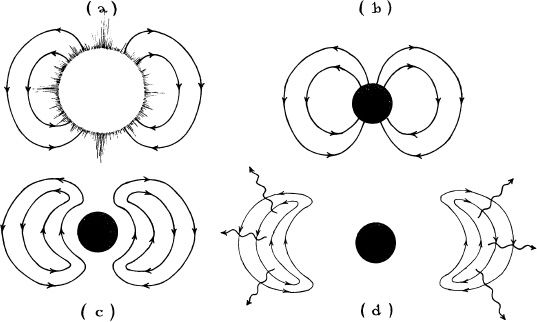
My first problem was a lulu: Take a bar magnet with a magnetic field threading through it and emerging from its two ends. The field consists of field lines, which children are taught to make visible using iron filings on a piece of paper with the magnet below it (Figure 7.1a). Adjacent field lines repel each other. (Their repulsion is felt when one pushes the north poles of two magnets toward each other.) Each magnet’s field lines are held together, despite their mutual repulsion, by the magnet’s iron. Remove the iron, and their repulsion will make the field lines explode (Figure 7.tb). All this was familiar to me from my undergraduate studies. Wheeler reminded me of it in a long, private discussion in his Princeton office. He then described a recent discovery by his friend Professor Mael Melvin at Florida State University in Tallahassee.
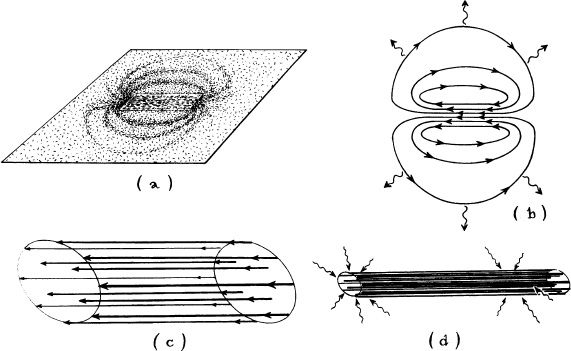
7.1 (a) The magnetic field lines around a bar magnet, made visible by iron filings on a piece of paper with the magnet below it. (b) The same field lines, with the paper and the magnet removed. Pressure between adjacent field lines makes them explode in the directions of the wavy arrows. (c) An infinitely long, cylindrical bundle of magnetic field lines whose field is so intense that its energy creates enough spacetime curvature (gravity) to hold the bundle together, despite the repulsion between field lines. (d) Wheeler’s conjecture that when the bundle of field lines in (c) is squeezed slightly, its gravity would become so strong as to compress the bundle into implosion (wiggly lines).
Melvin had shown, using Einstein’s field equation, that not only can magnetic field lines be held together against explosion by the iron in a bar magnet, they can also be held together by gravity without the aid of any magnet. The reason is simple: The magnetic field has energy, and its energy gravitates. [To see why the energy gravitates, recall that energy and mass are “equivalent” (Box 5.2): It is possible to convert mass of any sort (uranium, hydrogen, or whatever) into energy; and conversely, it is possible to convert energy of any sort (magnetic energy, explosive energy, or whatever) into mass. Thus, in a deep sense, mass and energy are merely different names for the same thing, and this means that, since all forms of mass produce gravity, so must all forms of energy. The Einstein field equation, when examined carefully, insists on it.] Now, if we have an enormously intense magnetic field—a field far more intense than ever encountered on Earth—then the field’s intense energy will produce intense gravity, and that gravity will compress the field; it will hold the field lines together despite the pressure between them (Figure 7.1c). This was Melvin’s discovery.
Wheeler’s intuition told him that such “gravitationally bundled” field lines might be as unstable as a pencil standing on its tip: Push the pencil slightly, and gravity will make it fall. Compress the magnetic field lines slightly, and gravity might overwhelm their pressure, pulling them into implosion (Figure 7.1d). Implosion to what? Perhaps to form an infinitely long, cylindrical black hole; perhaps to form a naked singularity (a singularity without an enshrouding horizon).
It did not matter to Wheeler that magnetic fields in the real Universe are too weak for gravity to hold them together against explosion. Wheeler’s quest was not to understand the Universe as it exists, but rather to understand the fundamental laws that govern the Universe. By posing idealized problems which push those laws to the extreme, he expected to gain new insights into the laws. In this spirit, he offered me my first gravitational research problem: Use the Einstein field equation to try to deduce whether Melvin’s bundle of magnetic field lines will implode, and if so, to what.
For many months I struggled with this problem. The scene of the daytime struggle was the attic of Palmer Physical Laboratory in Princeton, where I shared a huge office with other physics students and we shared our problems with each other, in a camaraderie of verbal give-and-take. The nighttime struggle was in the tiny apartment, in a converted World War 11 army barracks, where I lived with my wife, Linda (an artist and mathematics student), our baby daughter, Kares, and our huge collie dog, Prince. Each day I carried the problem back and forth with me between army barracks and laboratory attic. Every few days I collared Wheeler for advice. I beat at the problem with pencil and paper; I beat at it with numerical calculations on a computer; I beat at it in long arguments at the blackboard with my fellow students; and gradually the truth became clear. Einstein’s equation, pummeled, manipulated, and distorted by my beatings, finally told me that Wheeler’s guess was wrong. No matter how hard one might squeeze it, Melvin’s cylindrical bundle of magnetic field lines will always spring back. Gravity can never overcome the field’s repulsive pressure. There is no implosion.
This was the best possible result, Wheeler explained to me enthusiastically: When a calculation confirms one’s expectations, one merely firms up a bit one’s intuitive understanding of the laws of physics. But when a calculation contradicts expectations, one is on the way toward new insight.
The contrast between a spherical star and Melvin’s cylindrical bundle of magnetic field lines was extreme, Wheeler and I realized: When a spherical star is very compact, gravity inside it overwhelms any and all internal pressure that the star can muster. The implosion of massive, spherical stars is compulsory (Chapter 5 ). By contrast, regardless of how hard one squeezes a cylindrical bundle of magnetic field lines, regardless of how compact one makes the bundle’s circular cross section (Figure 7.1d), the bundle’s pressure will always overcome gravity and push the field lines back outward. The implosion of cylindrical magnetic field lines is forbidden; it can never occur.
Why do spherical stars and a cylindrical magnetic field behave so differently? Wheeler encouraged me to probe this question from every possible direction; the answer might bring deep insight into the laws of physics. But he did not tell me how to probe. I was becoming an independent researcher; it would be best, he believed, for me to develop my own research strategy without further guidance from him. Independence breeds strength.
From 1963 to 1972, through most of the golden age, I struggled to understand the contrast between spherical stars and cylindrical magnetic fields, but only in fits and starts. The question was deep and difficult, and there were other, easier issues to study with most of my effort: the pulsations of stars, the gravitational waves that stars should emit when they pulsate, the effects of spacetime curvature on huge clusters of stars and on their implosion. Amidst those studies, once or twice a year I would pull from my desk drawer the stacks of manila folders containing my magnetic field calculations. Gradually I augmented those calculations with computations of other idealized infinitely long, cylindrical objects: cylindrical “stars” made of hot gas, cylindrical clouds of dust that implode, or that spin and implode simultaneously. Although these objects do not exist in the real Universe, my calculations about them, done in fits and starts, gradually brought understanding.
By 1972 the truth was evident: Only if an object is compressed in all three of its spatial directions, north–south, east–west, and up–down (for example, if it is compressed spherically), can gravity become so strong that it overwhelms all forms of internal pressure. If, instead, the object is compressed in only two spatial directions (for example, if it is compressed cylindrically into a long thin thread), gravity grows strong, but not nearly strong enough to win the battle with pressure. Very modest pressure, whether due to hot gas, electron degeneracy, or magnetic field lines, can easily overwhelm gravity and make the cylindrical object explode. And if the object is compressed in only a single direction, into a very thin pancake, pressure will overwhelm gravity even more easily.
My calculations showed this clearly and unequivocally in the case of spheres, infinitely long cylinders, and infinitely extended pancakes. For such objects, the calculations were manageable. Much harder to compute—indeed, far beyond my talents—were nonspherical objects of finite size. But physical intuition emerging from my calculations and from calculations by my youthful comrades told me what to expect. That expectation I formulated as a hoop conjecture:
Take any kind of object you might wish—a star, a cluster of stars, a bundle of magnetic field lines, or whatever. Measure the object’s mass, for example, by measuring the strength of its gravitational pull on orbiting planets. Compute from that mass the object’s critical circumference (18.5 kilometers times the object’s mass in units of the mass of the Sun). If the object were spherical (which it is not) and were to implode or be squeezed, it would form a black hole when it gets compressed inside this critical circumference. What happens if the object is not spherical? The hoop conjecture purports to give an answer (Figure 7.2).
Construct a hoop with circumference equal to the critical circumference of your object. Then try to place the object at the center of the hoop, and try to rotate the hoop completely around the object. If you succeed, then the object must already have created a black-hole horizon around itself. If you fail, then the object is not yet compact enough to create a black hole.
In other words, the hoop conjecture claims that, if an object (a star, a star cluster, or whatever) gets compressed in a highly nonspherical manner, then the object will form a black hole around itself when, and only when, its circumference in all directions has become less than the critical circumference.
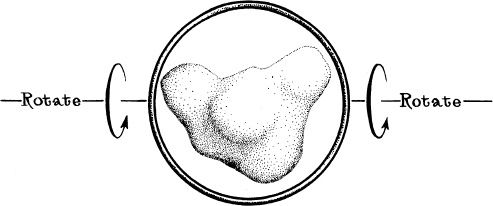
7.2 According to the hoop conjecture, an imploding object forms a black hole when, and only when, a hoop with the critical circumference can be placed around the object and rotated.
I proposed this hoop conjecture in 1972. Since then, I and others have tried hard to learn whether it is correct or not. The answer is buried in Einstein’s field equation, but to extract the answer has proved exceedingly difficult. In the meantime, circumstantial evidence in favor of the hoop conjecture has continued to mount. Most recently, in 1991, Stuart Shapiro and Saul Teukolsky at Cornell University have simulated, on a supercomputer, the implosion of a highly nonspherical star and have seen black holes form around the imploded star precisely when the hoop conjecture predicts it. If a hoop can be slipped over the imploded star and rotated, a black hole forms; if it cannot, there is no black hole. But only a few such stars were simulated and with special nonspherical shapes. We therefore still do not know for certain, nearly a quarter century after I proposed it, whether the hoop conjecture is correct, but it looks promising.
I gor Dmitrievich Novikov in many ways was my Soviet counterpart, just as Yakov Borisovich Zel’dovich was Wheeler’s. In 1962, when I was first meeting Wheeler and embarking on my career under his mentorship, Novikov was first meeting Zel’dovich and becoming a member of his research team.
Whereas I had had a simple and supportive early life—born and reared in a large, tightly knit Mormon family 2 in Logan, Utah—Igor Novikov had had it rough. In 1937, when Igor was two, his father, a high official in the Railway Ministry in Moscow, was entrapped by Stalin’s Great Terror, arrested, and (less lucky than Landau) executed. His mother’s life was spared; she was sent to prison and then exile, and Igor was reared by an aunt. (Such Stalin-era family tragedies were frightfully common among my Russian friends and colleagues.)
In the early 1960s, while I was studying physics as an undergraduate at Caltech, Igor was studying it as a graduate student at Moscow University.
In 1962, when I was preparing to go to Princeton for graduate study and do general relativity research with John Wheeler, one of my Caltech professors warned me against this course: General relativity has little relevance for the real Universe, he warned; one should look elsewhere for interesting physics challenges. (This was the era of widespread skepticism about black holes and lack of interest in them.) At this same time, in Moscow, Igor was completing his kandidat degree (Ph.D.) with a specialty in general relativity, and his wife, Nora, also a physicist, was being warned by friends that relativity was a backwater with no relevance to the real Universe. Her husband, for the sake of his career, should leave it.
While I was ignoring these warnings and pushing onward to Princeton, Nora, worried by the warnings, seized an opportunity at a physics conference in Estonia to get advice from the famous physicist Yakov Borisovich Zel’dovich. She sought Zel’dovich out and asked whether he thought general relativity was of any importance. Zel’dovich, in his dynamic, forceful way, replied that relativity was going to become extremely important for astrophysics research. Nora then described an idea on which her husband was working, the idea that the implosion of a star to form a black hole might be similar to the big-bang origin of our Universe, but with time turned around and run backward. 3 As Nora spoke, Zel’dovich became more and more excited. He himself had developed the same idea and was exploring it.
A few days later, Zel’dovich barged into an office that Igor Novikov shared with many other students at Moscow University’s Shternberg Astronomical Institute, and began grilling Novikov about his research. Though their ideas were similar, their research methods were completely different. Novikov, already a great expert in relativity, had used an elegant mathematical calculation to demonstrate the similarity between the big bang and stellar implosion. Zel’dovich, who knew hardly any relativity, had demonstrated it using deep physical insight and crude calculations. Here was an ideal match of talents, Zel’dovich realized. He was just then emerging from his life as an inventor and designer of nuclear weapons and was beginning to build a new team of researchers, a team to work on his newfound love: astrophysics. Novikov, as a master of general relativity, would be an ideal member of the team.
When Novikov, happy at Moscow University, hesitated to sign up, Zel’dovich exerted pressure. He went to Mstislav Keldysh, the director of the Institute of Applied Mathematics where Zel’dovich’s team was being assembled; Keldysh telephoned 1van Petrovsky, the Rektor (president) of Moscow University, and Petrovsky sent for Novikov. With trepidation Novikov entered Petrovsky’s office, high in the central tower of the University, a place to which Novikov had never imagined venturing. Petrovsky was unequivocal: “Maybe you now don’t want to leave the University to work with Zel’dovich, but you will want to.” Novikov signed up, and despite some difficult times, never regretted it.
Zel’dovich’s style as a mentor for young astrophysicists was the one he had developed while working with his nuclear weapons design team: “Zel’dovich’s sparks [ideas] and his team’s gasoline”—unless, perchance, some other member of the team could compete in inventing ideas (as Novikov usually did, when relativity was involved). Then Zel’dovich would enthusiastically take up his young colleague’s idea and knock it about with the team in a vigorous thrust and parry, bringing the idea quickly to maturity and making it the joint property of himself and its inventor.
Novikov has described Zel’dovich’s style vividly. Calling his mentor by first name plus abbreviated patronymic (a form of Russian address that is simultaneously respectful and intimate), Novikov says: “Yakov Boris’ch would often awaken me by telephone at five or six in the morning. T have a new idea! a new idea! Come to my apartment! Let’s talk!’ I would go, and we would talk for a long, long time. Yakov Boris’ch thought we all could work as long as he. He would work with his team from six in the morning to, say, ten, on one subject. Then a new subject until lunch. After lunch we would take a small walk or exercise or a short nap. Then coffee and more interaction until five or six. In the evening we were freed to calculate, think, or write, in preparation for the next day.”
Coddled in his weapons design days, Zel’dovich continued to demand that the world adjust to him: follow his schedule, start work when he started, nap when he napped. (In 1968, John Wheeler, Andrei Sakharov, and I spent an afternoon discussing physics with him in a hotel room in the deep south of the Soviet Union. After several hours of intense discussion, Zel’dovich abruptly announced that it was time to nap. He then laid down and slept for twenty minutes, while Wheeler, Sakharov, and I relaxed and read quietly in our respective corners of the room, waiting for him to awaken.)
Impatient with perfectionists like me, who insist on getting all the details of a calculation right, Zel’dovich cared only about the main concepts. Like Oppenheimer, he could scatter irrelevant details to the winds and zero in, almost unerringly, on the central issues. A few arrows and curves on the blackboard, an equation not longer than half a line, a few sentences of vivid prose, with these he would bring his team to the heart of a research problem.
He was quick to judge an idea or a physicist’s worth, and slow to change his judgments. He could retain faith in a wrong snap judgment for years, thereby blinding himself to an important truth, as when he rejected the idea that tiny black holes can evaporate (Chapter 12 ). But when (as was usually the case) his snap judgments were right, they enabled him to move forward across the frontiers of knowledge at a tremendous pace, faster than anyone I have ever met.
The contrast between Zel’dovich and Wheeler was stark: Zel’dovich whipped his team into shape with a firm hand, a constant barrage of his own ideas, and joint exploitation of his team’s ideas. Wheeler offered his fledglings a philosophical ambience, a sense that there were exciting ideas all around, ready for the plucking; but he rarely pressed an idea, in concrete form, onto a student, and he absolutely never joined his students in exploiting their ideas. Wheeler’s paramount goal was the education of his fledglings, even if that slowed the pace of discovery. Zel’dovich—still infused with the spirit of the race for the superbomb—sought the fastest pace possible, whatever the expense.
Zel’dovich was on the telephone at ungodly hours of the morning, demanding attention, demanding interaction, demanding progress. Wheeler seemed to us, his fledglings, the busiest man in the world; far too busy with his own projects to demand our attention. Yet he was always available at our request, to give advice, wisdom, encouragement.

left: John Archibald Wheeler, ca. 1970. right: Igor Dmitrievich Novikov and Yakov Borisovich Zel’dovich in 1962. [left: courtesy Joseph Henry Laboratories, Princeton University; right: courtesy S. Chandrasekhar;]

Dennis Sciama in 1955. [courtesy Dennis W. Sciama.]
D ennis Sciama, the third great mentor of the era, had yet another style. He devoted the 1960s and early 1970s almost exclusively to providing an optimal environment for his Cambridge University students to grow in. Because he relegated his own personal research and career to second place, after those of his students, he was never promoted to the august position of “Professor” at Cambridge (a position much higher than being a professor in America). It was his students, far more than he, who reaped the rewards and the kudos. By the end of the 1970s two of his former students, Stephen Hawking and Martin Rees, were Cambridge Professors.
Sciama was a catalyst; he kept his students closely in touch with the most important new developments in physics, worldwide. Whenever an interesting discovery was published, he would assign a student to read and report on it to the others. Whenever an interesting lecture was scheduled in London, he would take or send his entourage of students down on the train to hear it. He had exquisitely good sense about what ideas were interesting, what issues were worth pursuing, what one should read in order to get started on any research project, and whom one should go to for technical advice.
Sciama was driven by a desperate desire to know how the Universe is made. He himself described this drive as a sort of metaphysical angst. The Universe seemed so crazy, bizarre, and fantastic that the only way to deal with it was to try to understand it, and the best way to understand it was through his students. By having his students solve the most challenging problems, he could move more quickly from issue to issue than if he paused to try to solve them himself.
Black Holes Have No Hair
A mong the discoveries of the golden age, one of the greatest was that “a black hole has no hair.” (The meaning of this phrase will become clear gradually in the coming pages.) Some discoveries in science are made quickly, by individuals; others emerge slowly, as a result of diverse contributions from many researchers. The hairlessness of black holes was of the second sort. It grew out of research by the intellectual progeny of all three great mentors, Zel’dovich, Wheeler, and Sciama, and out of research by many others. In the following pages, we shall watch as this myriad of researchers struggles step by step, bit by bit, to formulate the concept of a black hole’s hairlessness, prove it, and grasp its implications.
The first hints that “a black hole has no hair” came in 1964, from Vitaly Lazarevich Ginzburg, the man who had invented the LiD fuel for the Soviet hydrogen bomb, and whose wife’s alleged complicity in a plot to kill Stalin had freed him from further bomb design work (Chapter 6 ). Astronomers at Caltech had just discovered quasars, enigmatic, explosive objects in the most distant reaches of the Universe, and Ginzburg was trying to understand how quasars might be powered (Chapter 9 ). One possibility, Ginzburg thought, might be the implosion of a magnetized, supermassive star to form a black hole. The magnetic field lines of such a star would have the shape shown in the upper part of Figure 7.3a—the same shape as the Earth’s magnetic field lines. As the star implodes, its field lines might become strongly compressed and then explode violently, releasing huge energy, Ginzburg speculated; and this might help to explain quasars.

Left: Vitaly Lazarevich Ginzburg (ca. 1962), the person who produced the first evidence for the “no-hair conjecture.” Right: Werner Israel (in 1964), the person who devised the first rigorous proof that the “no-hair conjecture” is correct. [Left: courtesy Vitaly Ginzburg; right: courtesy Werner Israel.]
To test this speculation by computing the full details of the star’s implosion would have been exceedingly difficult, so Ginzburg did the second best thing. Like Oppenheimer in his first crude exploration of what happens when a star implodes (Chapter 6 ), Ginzburg examined a sequence of static stars, each one more compact than the previous one, and all with the same number of magnetic field lines threading through their interiors. This sequence of static stars should mimic a single imploding star, Ginzburg reasoned. Ginzburg derived a formula that described the shapes of the magnetic field lines for each of the stars in his sequence—and found a great surprise. When a star was nearly at its critical circumference and beginning to form a black hole around itself, its gravity sucked its magnetic field lines down onto its surface, plastering them there tightly. When the black hole was formed, the plastered-down field lines were all inside its horizon. No field lines remained, sticking out of the hole (Figure 7.3a). This did not bode well for Ginzburg’s idea of how to power quasars, but it did suggest an intriguing possibility: When a magnetized star implodes to form a black hole, the hole might well be born with no magnetic field whatsoever.
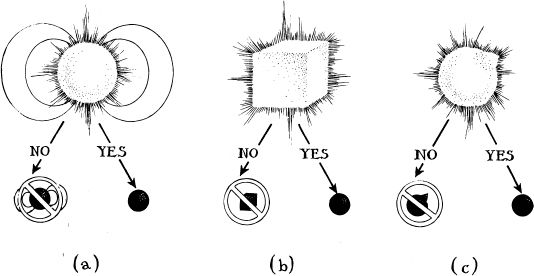
7.3 Some examples of the “no-hair conjecture”: (a) When a magnetized star implodes, the hole it forms has no magnetic field. (b) When a square star implodes, the hole it forms is round, not square. (c) When a star with a mountain on its surface implodes, the hole it forms has no mountain.
At about the time that Ginzburg was making this discovery, only a few kilometers away in Moscow Zel’dovich’s team—with Igor Novikov and Andrei Doroshkevich taking the lead—began to ask themselves, “Since a round star produces a round hole when it implodes, will a deformed star produce a deformed hole?” As an extreme example, will a square star produce a square hole? (Figure 7.3b). To compute the implosion of a hypothetical square star would be exceedingly difficult, so Doroshkevich, Novikov, and Zel’dovich focused on an easier example: When a nearly spherical star implodes with a tiny mountain sticking out of its surface, will the hole it forms have a mountain-like protrusion on its horizon? By asking about nearly spherical stars with tiny mountains, the Zel’dovich team could simplify their calculations greatly; they could use mathematical techniques called perturbation methods that John Wheeler and a postdoc, Tullio Regge, had pioneered a few years earlier. These perturbation methods, which are explained a bit in Box 7.1, were carefully designed for the study of any small “perturbation” (any small disturbance) of an otherwise spherical situation. The gravitational distortion due to a tiny mountain on the Zel’dovich team’s star was just such a perturbation.
Doroshkevich, Novikov, and Zel’dovich simplified their calculation still further by the same trick that Oppenheimer and Ginzburg used: Instead of simulating the full, dynamical implosion of a mountain-endowed star, they examined only a sequence of static, mountainous stars, each one more compact than the one before. With this trick, and with perturbation techniques, and with intensive give-and-take amongst themselves, Doroshkevich, Novikov, and Zel’dovich quickly discovered a remarkable result: When a static, mountain-endowed star is small enough to form a black hole around itself, the hole’s horizon must be precisely round, with no protrusion (Figure 7.3c).
Similarly, it was tempting to conjecture that if an imploding square star were to form a black hole, its horizon would also be round, not square (Figure 7.3b). If this conjecture was correct, then a black hole should bear no evidence whatsoever of whether the star that created it was square, or round, or mountain-endowed, and also (according to Ginzburg) no evidence of whether the star was magnetized or free of magnetism.
A few years later, as this conjecture was gradually turning out to be correct, John Wheeler invented a pithy phrase to describe it: A black hole has no hair- —the hair being anything that might stick out of the hole to reveal the details of the star from which it was formed.
Box 7.1
An Explanation of Perturbation Methods, for Readers Who Like Algebra
In algebra one learns to compute the square of a sum of two numbers, a and b, from the formula
(a + b) 2 = a 2 + 2ab + b 2 .
Suppose that a is a huge number, for example 1000, and that b is very small by comparison, for example 3. Then the third term in this formula, b 2 , will be very small compared to the other two and thus can be thrown away without making much error:
| (1000+ 3) 2 | = | 1000 2 + 2 × 1000 × 3 + 3 2 = 1,006,009 |
| 1000 2 + 2 × 1000 × 3 = 1,006,000. |
Perturbation methods are based on this approximation. The a = 1000 is like a precisely spherical star, b = 3 is like the star’s tiny mountain, and (a + b) 2 is like the spacetime curvature produced by the star and mountain together. In computing that curvature, perturbation methods keep only effects that are linear in the mountain’s properties (effects like 2ab = 6000, which is linear in b = 3); these methods throw away all other effects of the mountain (effects like b 2 = 9). So long as the mountain remains small compared to the star, perturbation methods are highly accurate. However, if the mountain were to grow as big as the rest of the star (as it would need to do to make the star square rather than round), then perturbation methods would produce serious errors—errors like those in the above formulas with a = 1000 and b = 1000:
| (1000+1000) 2 | = | 1000 2 + 2 × 1000 × 1000 + 1000 2 = 4,000,000 |
| 1000 2 + 2 × 1000 × 1000 = 3,000,000. |
These two results differ significantly.
It is hard for most of Wheeler’s colleagues to believe that this conservative, highly proper man was aware of his phrase’s prurient interpretation. But I suspect otherwise; I have seen his impish streak, in private, on rare occasion. 4 Wheeler’s phrase quickly took hold, despite resistance from Simon Pasternak, the editor-in-chief of the Physical Review, the journal in which most Western black-hole research is published. When Werner Israel tried to use the phrase in a technical paper in late 1969, Pasternak fired off a peremptory note that under no circumstances would he allow such obscenities in his journal. But Pasternak could not hold back for long the flood of “no-hair” papers. In France and the U.S.S.R., where the French- and Russian-language translations of Wheeler’s phrase were also regarded as unsavory, the resistance lasted longer. By the late 1970s, however, Wheeler’s phrase was being used and published by physicists worldwide, in all languages, without even a flicker of a childish grin.
I t was the winter of 1964–65 by the time Ginzburg, and Dorosh-kevich, Novikov, and Zel’dovich, had invented their no-hair conjecture and mustered their evidence for it. Once every three years, experts on general relativity gathered somewhere in the world for a one-week scientific conference to exchange ideas and show each other the results of their researches. The fourth such conference would be held in London in June.
Nobody on Zel’dovich’s team had ever traveled beyond the borders of the Communist bloc of nations. Zel’dovich himself would surely not be allowed to go; his contact with weapons research was much too recent. Novikov, however, was too young to have been involved in the hydrogen bomb project, his knowledge of general relativity was the best of anyone on the team (which is why Zel’dovich had recruited him onto the team in the first place), he was now the team’s captain (Zel’-dovich was the coach), and his English was passable though far from fluent. He was the logical choice.
This was a good period in East–West relations. Stalin’s death a dozen years earlier had triggered a gradual resumption of correspondence and visits between Soviet scientists and their Western colleagues (though not nearly so free a correspondence or visits as in the 1920s and early 1930s before Stalin’s iron curtain descended). As a matter of course, the Soviet Union was now sending a small delegation of scientists to every major international conference; such delegations were important not only for maintaining the strength of Soviet science, but also for demonstrating the Soviets’ strength to Western scientists. Since the time of the tsars, Russian bureaucrats have had an inferiority complex with respect to the West; it is very important for them to be able to hold their heads up in Western public view and show with pride what their nation can do.
Thus it was that Zel’dovich, having arranged an invitation from London for Novikov to give one of the major lectures of the Relativity Conference, found it easy to convince the bureaucrats to include his young colleague in the Soviet delegation. Novikov had many impressive things to report; he would create a very positive impression of the strength of Soviet physics.
In London, Novikov presented a one-hour lecture to an audience of three hundred of the world’s leading relativity physicists. His lecture was a tour de force. The results on the gravitational implosion of a mountain-endowed star were but one small part of the lecture; the remainder was a series of equally major contributions to our understanding of relativistic gravity, neutron stars, stellar implosion, black holes, the nature of quasars, gravitational radiation, and the origin of the Universe. As I sat there in London listening to Novikov, I was stunned by the breadth and power of the Zel’dovich team’s research. I had never before seen anything like it.
After Novikov’s lecture, I joined the enthusiastic crowd around him and discovered, much to my pleasure, that my Russian was slightly better than his English and that I was needed to help with translating the discussion. As the crowd thinned, Novikov and I went off together to continue our discussion privately. Thus began one of my finest friendships.
I t was not possible for me or anyone else to absorb fully in London the details of the Zel’dovich team’s no-hair analysis. The details were too complex. We had to await a written version of the work, one in which the details were spelled out with care.
The written version arrived in Princeton in September 1965, in Russian. Once again I was thankful for the many boring hours I had spent in Russian class as an undergraduate. The written analysis contained two pieces. The first piece, clearly the work of Doroshkevich and Novikov, was a mathematical proof that, when a static star with a tiny mountain is made more and more compact, there are just two possible outcomes. Either the star creates a precisely spherical hole around itself, or else the mountain produces such enormous spacetime curvature, as the star nears its critical circumference, that the mountain’s effects are no longer a “small perturbation”; the method of calculation then fails, and the outcome of the implosion is unknown. The second piece of the analysis was what I soon learned to identify as a “typical Zel’dovich” argument: If the mountain initially is tiny, it is intuitively obvious that the mountain cannot produce enormous curvature as the star nears its critical circumference. We must discard that possibility. The other possibility must be the truth: The star must produce a precisely spherical hole.
What was intuitively obvious to Zel’dovich (and would ultimately turn out to be true) was far from obvious to most Western physicists. Controversy began to swirl.
The power of a controversial research result is enormous. It attracts physicists like picnics attract ants. Thus it was with the Zel’dovich team’s no-hair evidence. The physicists, like ants, came one by one at first, but then in droves.
T he first was Werner Israel, born in Berlin, reared in South Africa, trained in the laws of relativity in Ireland, and now struggling to start a relativity research group in Edmonton, Canada. In a mathematical tour de force, Israel improved on the first, Doroshkevich–Novikov, part of the Soviet proof: He treated not just tiny mountains, as had the Soviets, but mountains of any size and shape. In fact, his calculations worked correctly for any implosion, no matter how nonspherical, even a square one, and they allowed the implosion to be dynamical, not just an idealized sequence of static stars. Equally remarkable was Israel’s conclusion, which was similar to the Doroshkevich–Novikov conclusion, but far stronger: A highly nonspherical implosion can have only two outcomes: either it produces no black hole at all, or else it produces a black hole that is precisely spherical For this conclusion to be true, however, the imploding body had to have two special properties: It must be completely devoid of any electric charge, and it must not spin at all. The reasons will become clear below.
Israel first presented his analysis and results on 8 February 1967, at a lecture at Kings College in London. The title of the lecture was a little enigmatic, but Dennis Sciama in Cambridge urged his students to journey down to London and hear it. As George Ellis, one of the students, recalls, “It was a very, very interesting lecture. Israel proved a theorem that came totally out of the blue; it was totally unexpected; nothing remotely like it had ever been done before.” When Israel brought his lecture to a close, Charles Misner (a former student of Wheeler’s) rose to his feet and offered a speculation: What happens if the imploding star spins and has electric charge? Might there again be just two possibilities: no hole at all, or a hole with a unique form, determined entirely by the imploding star’s mass, spin, and charge? The answer would ultimately turn out to be yes, but not until after Zel’dovich’s intuitive insight had been tested.
Z el’dovich, Doroshkevich, and Novikov, you will recall, had studied not highly deformed stars, but rather nearly spherical stars, with small mountains. Their analysis and Zel’dovich’s claims triggered a plethora of questions:
If an imploding star has a tiny mountain on its surface, what is the implosion’s outcome? Does the mountain produce enormous spacetime curvature, as the star nears its critical circumference (the outcome rejected by Zel’dovich’s intuition)? Or does the mountain’s influence disappear, leaving behind a perfectly spherical black hole (the outcome Zel’dovich favored)? And if a perfectly spherical hole is formed, how does the hole manage to rid itself of the mountain’s gravitational influence? What makes the hole become spherical?
As one of Wheeler’s students, I pondered these questions. However, I pondered them not as a challenge for myself, but rather as a challenge for my own students. It was now 1968; I had completed my Ph.D. at Princeton and had returned to my alma mater, Caltech, first as a postdoc and now as a professor; and I was beginning to build around myself an entourage of students similar to Wheeler’s at Princeton.
Richard Price, a rough-bearded, two-hundred-pound, physically powerful young man from Brooklyn with a black belt in karate, had already worked with me on several small research projects, including one using the kind of mathematical methods needed to answer these questions: perturbations methods. He was now mature enough to tackle a more challenging project. The test of Zel’dovich’s intuition looked ideal, but for one thing. It was a hot topic; others elsewhere were struggling with it; the ants were beginning to attack the picnic in droves. Price would have to move fast.
He didn’t. Others beat him to the answers. He got there third, after Novikov and after Israel, but he got there more firmly, more completely, with deeper insight.
Price’s insight was immortalized by Jack Smith, a humorous columnist for the Los Angeles Times. In the 27 August 1970 issue of the Times, Smith described a visit the previous day to Caltech: “After luncheon at the Faculty Club I walked alone around the campus. I could feel the deep thought in the air. Even in summer it stirs the olive trees. I looked in a window. A blackboard was covered with equations, thick as leaves on a walk, and three sentences in English: Price’s Theorem: Whatever can be radiated is radiated Schutz’s Obseroation: Whatever is radiated can be radiated Things can be radiated if and only if they are radiated. I walked on, wondering how it will affect Caltech this fall when they let girls in as freshmen for the first time. I don’t think they’ll do the place a bit of harm ... I have a hunch they’ll radiate.”
This quote requires some explanation. “Schutz’s observation” was facetious, but Price’s theorem, “Whatever can be radiated is radiated,” was a serious confirmation of a 1969 speculation by Roger Penrose.
Price’s theorem is illustrated by the implosion of a mountain-endowed star. Figure 7.4 depicts the implosion. The left half of this figure is a spacetime diagram of the type introduced in Figure 6.7 of Chapter 6 ; the right side is a sequence of snapshots of the star’s and horizon’s shape as time passes, with the earliest times at the bottom and the latest at the top.
As the star implodes (bottom two snapshots in Figure 7.4), its mountain grows larger, producing a growing, mountain-shaped distortion in the star’s spacetime curvature. Then, as the star sinks inside its critical circumference and creates a black hole horizon around itself (middle snapshot), the distorted spacetime curvature deforms the horizon, giving it a mountain-like protrusion. The horizon’s protrusion, however, cannot live long. The stellar mountain that generated it is now inside the hole, so the horizon can no longer feel the mountain’s influence. The horizon is no longer being forced, by the mountain, to keep its protrusion. The horizon ejects the protrusion in the only way it can: It converts the protrusion into ripples of spacetime curvature (gravitational waves—Chapter 10 ) that propagate away in all directions (top two snapshots). Some of the ripples go down the hole, others fly out into the surrounding Universe, and as they fly away, the ripples leave the hole with a perfectly spherical shape
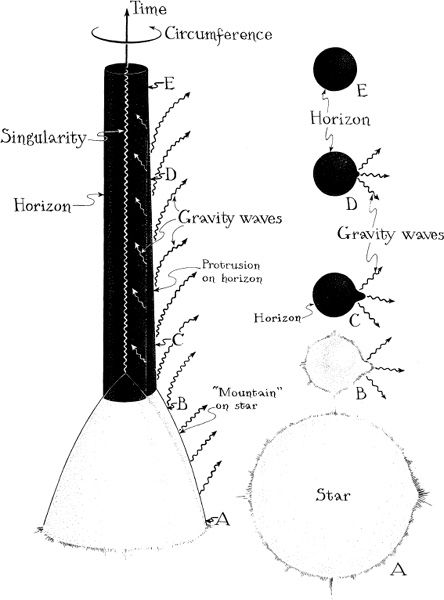
7.4 Spacetime diagram ( left ) and a sequence of snapshots (right) showing the implosion of a mountain-endowed star to form a black hole.
A familiar analogue is the plucking of a violin string. So long as one’s finger holds the string in a deformed shape, it remains deformed; so long as the mountain is protruding out of the hole, it keeps the newborn horizon deformed. When one removes one’s finger from the string, the string vibrates, sending sound waves out into the room; the sound waves carry away the energy of the string’s deformation, and the string settles down into an absolutely straight shape. Similarly, when the mountain sinks inside the hole, it can no longer keep the horizon deformed, so the horizon vibrates, sending off gravitational waves; the waves carry away the energy of the horizon’s deformation, and the horizon settles down into an absolutely spherical shape.
How does this mountain-endowed implosion relate to Price’s theorem? According to the laws of physics, the horizon’s mountain-like protrusion can be converted into gravitational radiation (ripples of curvature). Price’s theorem tells us, then, that the protrusion must be converted into gravitational waves, and that this radiation must carry the protrusion completely away. This is the mechanism that makes the hole hairless.
Price’s theorem tells us not only how a deformed hole loses its deformation, but also how a magnetized hole loses its magnetic field (Figure 7.5). (The mechanism, in this case, was already clear before Price’s theorem from a computer simulation by Werner Israel and two of his Canadian students, Vicente de la Cruz and Ted Chase.) The magnetized hole is created by the implosion of a magnetized star. Before the horizon engulfs the imploding star (Figure 7.5a), the magnetic field is firmly anchored in the star’s interior; electric currents inside the star prevent the field from escaping. After the star is swallowed by the horizon (Figure 7.5b), the field can no longer feel the star’s electric currents; they no longer anchor it. The field now threads the horizon, rather than the star, but the horizon is a worthless anchor. The laws of physics permit the field to turn itself into electromagnetic radiation (ripples of magnetic and electric force), and Price’s theorem therefore demands that it do so (Figure 7.5c). The electromagnetic radiation flies away, partly down the hole and partly away from it, leaving the hole unmagnetized (Figure 7.5d).
7.5 A sequence of snapshots showing the implosion of a magnetized star (a) to form a black hole (b). The hole at first inherits the magnetic field from the star. However, the hole has no power to hold on to the field. The field slips off it (c), is converted into electromagnetic radiation, and flies away(d).
If, as we have seen, mountains can be radiated away and magnetic fields can be radiated away, then what is left? What cannot be turned into radiation? The answer is simple: Among the laws of physics there is a special set of laws called conservation laws. According to these conservation laws, there are certain quantities that can never oscillate or vibrate in a radiative manner, and that therefore can never be converted into radiation and be ejected from a black hole’s vicinity. These conserved quantities are the gravitational pull due to the hole’s mass, the swirl of space due to the hole’s spin (discussed below), and radially pointing electric field lines, that is, electric fields that point directly outward (discussed below) due to the hole’s electric charge. 5
Thus, according to Price’s theorem, the influences of the hole’s mass, spin, and charge are the only things that can remain behind when all the radiation has cleared away. All of the hole’s other features will be gone, carried away by the radiation. This means that no measurement one might ever make of the properties of the final hole can possibly reveal any features of the star that imploded to form it, except the star’s mass, spin, and charge. From the hole’s properties one cannot even discern (according to calculations by James Rartle and Jacob Beken stein, both Wheeler students) whether the star that formed the hole was made of matter or antimatter, of protons and electrons, or of neutrinos and antineutrinos. In Wheeler’s words, made more precise, a black hole has almost no hair; its only “hair” is its mass, its spin, and its electric charge.
T he firm, ultimate proof that a black hole has no hair (except its mass, spin, and electric charge) was actually not Price’s. Price’s analysis was restricted to imploding stars that are very nearly spherical, and that spin, if at all, only very slowly. The perturbation methods he used required this restriction. To learn the ultimate fate of a highly deformed, rapidly spinning, imploding star required a set of mathematical techniques very different from perturbation methods.
Dennis Sciama’s students at Cambridge University were masters of the required techniques, but the techniques were difficult; extremely so. It took fifteen years for Sciama’s students and their intellectual descendants, using those techniques, to produce a firm and complete proof that black holes have no hair—that even if a hole spins fast and is strongly deformed by its spin, the hole’s final properties (after all radiation has flown away) are uniquely fixed by the hole’s mass, spin, and charge. The lion’s share of the credit for the proof goes to two of Sciama’s students, Brandon Carter and Stephen Hawking, and to Werner Israel; but major contributions came also from David Robinson, Gary Bunting, and Pavel Mazur.
I n Chapter 3 , I commented on the great difference between the laws of physics in our real Universe and the society of ants in T. H. White’s epic novel The Once and Future King. White’s ants were governed by the motto “Everything not forbidden is compulsory,” but the laws of physics violate that motto flagrantly. Many things allowed by physical law are so highly improbable that they never occur. Price’s theorem is a remarkable exception. It is one of the few situations I have ever encountered in physics where the ants’ motto holds sway: If physical law does not forbid a black hole to eject something as radiation, then ejection is compulsory.
Equally unusual are the implications of a black hole’s resulting “hairless” state. Normally we physicists build simplified theoretical or computer models to try to understand the complicated Universe around us. As an aid to understanding weather, atmospheric physicists build computer models of the Earth’s circulating atmosphere. As an aid to understanding earthquakes, geophysicists build simple theoretical models of slipping rocks. As an aid to understanding stellar implosion, Oppenheimer and Snyder in 1939 built a simple theoretical model: an imploding cloud of matter that was perfectly spherical, perfectly homogeneous, and completely devoid of pressure. And as we physicists build all these models, we are intensely aware of their limitations. They are but pale images of the complexity that abounds “out there,” in the “real” Universe.
Not so for a black hole—or, at least, not so once the radiation has flown away, carrying off all the hole’s “hair.” Then the hole is so exceedingly simple that we can describe it by precise, simple mathematical formulas. We need no idealizations at all. Nowhere else in the macroscopic world (that is, on scales larger than a subatomic particle) is this true. Nowhere else is our mathematics expected to be so precise. Nowhere else are we freed from the limitations of idealized models.
Why are black holes so different from all other objects in the macroscopic Universe? Why are they, and they alone, so elegantly simple? If I knew the answer, it would probably tell me something very deep about the nature of physical laws. But I don’t know. Perhaps the next generation of physicists will figure it out.
Black Holes Spin and Pulsate
W hat are the properties of the hairless holes, which are described so perfectly by the mathematics of general relativity?
If a black hole is idealized as having absolutely no electric charge and no spin, then it is precisely the spherical hole that we met in previous chapters. It is described, mathematically? by Karl Schwarz-schild’s 1916 solution to Einstein’s field equation (Chapters 3 and 6 ).
When electric charge is dropped into such a hole, then the hole acquires just one new feature: electric field lines, which stick out of it radially like quills out of a hedgehog. If the charge is positive, then these electric field lines push protons away from the hole and attract electrons; if it is negative, then the field lines push electrons away and attract protons. Such a charge-endowed hole is described mathematically, with perfect precision, by a solution to Einstein’s field equation found by the German and Dutch physicists Hans Reissner in 1916 and Gunnar Nordstrom in 1918. However, nobody understood the physical meaning of Reissner’s and Nordström’s solution until 1960, when two of Wheeler’s students, John Graves and Dieter Brill, discovered that it describes a charged black hole.
Box 7.2
The Organization of Soviet and Western Science: Contrasts and Consequences
As I and my young physicist colleagues struggled to develop the hoop conjecture and to prove that black holes have no hair and to discover how they lose their hair, we also were discovering how very differently physics was organized in the U.S.S.R. than in Britain and America, and what profound effects those differences have. The lessons we learned may have some value in planning for the future, especially in the former Soviet Union, where all state institutions—scientific as well as governmental and economic—are now (1993) struggling to reorganize along Western lines. The Western model is not completely perfect, and the Soviet system was not uniformly bad!
In America and Britain there is a constant flow of young talent through a research group such as Wheeler’s or Sciama’s. Undergraduates may join the group for their last, senior year, but they then are sent away for graduate study. Graduate students join it for three to five years, and then are sent elsewhere for postdoctoral study. Postdocs join it for two or three years and then are sent away and expected either to start a research group of their own elsewhere (as I did at Caltech) or to join a small, struggling group elsewhere. Almost nobody in Britain or America, no matter how talented, is allowed to stay on in the nest of his or her mentor.
In the U.S.S.R., by contrast, outstanding young physicists (such as Novi-kov) usually remained in the nest of their mentor for ten, twenty, and sometimes even thirty or forty years. A great Soviet mentor like Zel’-dovich or Landau usually worked in an Institute of the Academy of Sciences, rather than in a university, so his teaching load was small or nonexistent; by keeping his best former students, he built around himself a permanent team of full-time researchers, which became tightly knit and extremely powerful, and which might even stay with him until the end of his career.
Some of my Soviet friends attributed this difference to the failings of the British/American system: Almost all great British or American physicists work at universities, where research is often subservient to teaching and where there are inadequate numbers of permanent positions available to permit building up a strong, lasting group of researchers. As a result, there have been no theoretical physics research groups in Britain or America that can pretend to be the equal of Landau’s group in the 1930s through 1950s, or of Zel’dovich’s group in the 1960s and 1970s. The West, in this sense, had no hope of competing with the Soviet Union.
Some of my American friends attributed the difference to the failings of the Soviet system: It was very difficult, logistically, to move from institute to institute and city to city in the U.S.S.R., so young physicists were forced to remain with their mentors; they had no opportunity to get out and start independent groups of their own. The result, the critics asserted, was a feudal system. The mentor was like a lord and his team like serfs, indentured for most of their careers. The lord and serfs were interdependent in a complex way, but there was no question who was boss. If the lord was a master craftsman like Zel’dovich or Landau, the lord/serf team could be richly productive. If the lord was authoritarian and not so outstanding (as was commonly the case), the result could be tragic: a waste of human talent and a miserable life for the serfs.
In the Soviet system, each great mentor such as Zel’dovich produced just one research team, albeit a tremendously powerful one, one unequaled anywhere in the West. By contrast, great American or British mentors like Wheeler and Sciama produce as their progeny many smaller and weaker research groups, scattered throughout the land, but those groups can have a large cumulative impact on physics. The American and British mentors have a constant influx of new, young people to help keep their minds and ideas fresh. In those rare cases where Soviet mentors wanted to start over afresh, they had to break their ties with their old team in a manner which could be highly traumatic.
This, in fact, was destined to happen to Zel’dovich: He began building his astrophysics team in 1961; by 1964 it was superior to any other theoretical astrophysics team anywhere in the world; then in 1978, soon after the golden age ended, came a traumatic, explosive split in which almost everybody in Zel’dovich’s team went one way and he went another, psychologically wounded but free from encumbrances, free to begin building afresh. Sadly, his rebuilding would not be successful. Never again would he surround himself with a team so talented and powerful as that which he, with Novikov’s assistance, had led. But Novikov, now an independent researcher, would come into his own in the 1980s as the talented leader of a reconstructed team.
We can depict the curvature of space around a charged black hole, and the hole’s electric field lines, using an embedding diagram (left half of Figure 7.6). This diagram is essentially the same as the one in the lower right of Figure 3.4, but with the star (black portion of Figure 3.4) removed because the star is inside the black hole and thus no longer has contact with the external Universe. Stated more carefully, this diagram depicts the equatorial “plane”—a two-dimensional piece of the hole’s space—outside the black hole, embedded in a flat, three-dimensional hyperspace. (For a discussion of the meaning of such diagrams, see Figure 3.3 and the accompanying text.) The equatorial “plane” is cut off at the hole’s horizon, so we are seeing only the hole’s exterior, not its interior. The horizon, which in reality is the surface of a sphere, looks like a circle in the diagram because we are seeing only its equator. The diagram shows the hole’s electric field lines sticking radially out of the horizon. If we look down on the diagram from above (right side of Figure 7.6), then we do not see the curvature of space, but we do see the electric field lines more clearly.
7.6 Electric field lines emerging from the horizon of an electrically charged black hole. Left: Embedding diagram. Right: View of the embedding diagram from above.
The effects of spin on a black hole were not understood until the late 1960s. The understanding came largely from Brandon Carter, one of Dennis Sciama’s students at Cambridge University.
When Carter joined Sciama’s group in autumn 1964, Sciama immediately suggested, as his first research problem, a study of the implosion of realistic, spinning stars. Sciama explained that all previous calculations of implosion had dealt with idealized, nonspinning stars, but that the time and tools now seemed right for an assault on the effects of spin. A New Zealander mathematician named Roy Kerr had just published a paper giving a solution of Einstein’s field equation that seemed to describe the spacetime curvature outside a spinning star. This was the first solution for a spinning star that anyone had ever found. Unfortunately, Sciama explained, it was a very special solution; it surely could not describe all spinning stars. Spinning stars have lots of “hair” (lots of properties such as complicated shapes and complicated internal motions of their gas), and Kerr’s solution did not have much “hair” at all: The shapes of its spacetime curvature were very smooth, very simple; too simple to correspond to typical spinning stars. Nevertheless, Kerr’s solution of Einstein’s field equation was a place to start.
Left: Roy Kerr ca. 1975. Right: Brandon Carter lecturing about black holes at a summer school in the French Alps in June 1972. [Left: courtesy Roy Kerr; right: photo by Kip Thorne.]
Few research problems have the immediate payoff that this one did: Within a year Carter had shown mathematically that Kerr’s solution describes not a spinning star, but rather a spinning black hole. (This discovery was also made, independently, by Roger Penrose in London, and by Robert Boyer in Liverpool and Richard Lindquist, a former student of Wheeler’s who was working at Wesleyan University in Middletown, Connecticut.) By the mid-1970s, Carter and others had gone on to show that Kerr’s solution describes not just one special type of spinning black hole, but rather every spinning black hole that can possibly exist.
The physical properties of a spinning black hole are embodied in the mathematics of Kerr’s solution, and Carter, by plumbing that mathematics, discovered just what those properties should be. One of the most interesting is a tornado-like swirl that the hole creates in the space around itself.
7.7 An embedding diagram showing the “tornado-like swirl” of space created by the spin of a black hole.
This swirl is depicted in the embedding diagram of Figure 7.7. The trumpet-horn-shaped surface is the hole’s equatorial sheet (a two-dimensional piece of the hole’s space), as embedded in a flat, three-dimensional hyperspace. The hole’s spin grabs hold of its surrounding space (the trumpet-horn surface) and forces it to rotate in a tornado-like manner, with speeds proportional to the lengths of the arrows on the diagram. Far from a tornado’s core the air rotates slowly, and, similarly, far from the hole’s horizon space rotates slowly. Near the tornado’s core the air rotates fast, and, similarly, near the horizon space rotates fast. At the horizon, space is locked tightly onto the horizon: It rotates at precisely the same rate as the horizon spins.
This swirl of space has an inexorable influence on the motions of particles that fall into the hole. Figure 7.8 shows the trajectories of two such particles, as viewed in the reference frame of a static, external observer—that is, in the frame of an observer who does not fall through the horizon and into the hole.
The first particle (Figure 7.Ba) is dropped gently into the hole. If the hole were not spinning, this particle, like the surface of an imploding star, would move radially inward faster and faster at first; but then, as observed by the static, external observer, it would slow its infall and become frozen right at the horizon. (Recall the “frozen stars” of Chapter 6 .) The hole’s spin changes this in a very simple way: The spin makes space swirl, and the swirl of space makes the particle, as it nears the horizon, rotate in lockstep with the horizon itself. The particle thereby becomes frozen onto the spinning horizon and, as seen by the static, external observer, it circles around and around with the horizon forever. (Similarly, when a spinning star implodes to form a spinning hole, as seen by a static, external observer the star’s surface “freezes” onto the spinning horizon, circling around and around with it forever.)
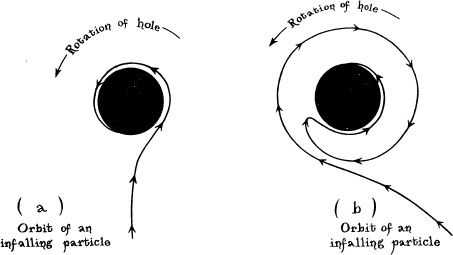
7.8 The trajectories in space of two particles that are thrown toward a black hole. (The trajectories are those that would be measured in a static, external reference frame.) Despite their very different initial motions, both particles are dragged, by the swirl of space, into precisely the same lockstep rotation with the hole as they near the horizon.
Though external observers see the particle of Figure 7.Ba freeze onto the spinning horizon and stay there forever, the particle itself sees something quite different. As the particle nears the horizon, gravitational time dilation forces the particle’s time to flow more and more slowly, compared with the time of a static, external reference frame. When an infinite amount of external time has passed, the particle has experienced only a finite and very small amount of time. In that finite time, the particle has reached the hole’s horizon, and in the next few moments of its time, it plunges right on through the horizon and down toward the hole’s center. This enormous difference between the particle’s infall as seen by the particle and as seen by external observers is completely analogous to the difference between a stellar implosion as seen on the star’s surface (rapid plunge through the horizon) and as seen by external observers (freezing of the implosion; last part of Chapter 6 ).
The second particle (Figure 7.Bb) is thrown toward the hole on an inspiraling trajectory that rotates oppositely to the hole’s spin. However, as the particle spirals closer and closer to the horizon, the swirl of space grabs hold of it and reverses its rotational motion. Like the first particle, it is forced into lockstep rotation with the horizon, as seen by external observers.
B esides creating a swirl in space, the spin of a black hole also distorts the hole’s horizon, in much the same way as the spin of the Earth distorts the Earth’s surface. Centrifugal forces push the spinning Earth’s equator outward a distance of 22 kilometers relative to its poles. Similarly, centrifugal forces make a black hole’s horizon bulge out at its equator in the manner depicted in Figure 7.9. If the hole does not spin, its horizon is spherical (left half of figure). If the hole spins rapidly, its horizon bulges out strongly (right half of figure).
If the hole were to spin extremely rapidly, centrifugal forces would tear its horizon apart much like they fling water out of a bucket when the bucket spins extremely rapidly. Thus, there is some maximum spin rate at which the hole can survive. The hole on the right half of Figure 7.9 is spinning at 58 percent of this maximum.
Is it possible to spin a hole up beyond its maximum allowed rate, and thereby destroy the horizon and catch a glimpse of what is inside? Unfortunately not. In 1986, a decade after the golden age, Werner Israel showed that, if one tries to make the hole spin faster than its maximum by any method at all, one will always fail. For example, if one tries to speed up a maximally spinning hole by throwing fast-spinning matter into it, centrifugal forces will prevent the fast-spinning matter from reaching the horizon and entering the hole. More to the point, perhaps, any tiny random interaction of a maximally spinning hole with the surrounding Universe (for example, the gravitational pull of distant stars) acts to slow the spin a bit. The laws of physics, it seems, don’t want to let anyone outside the hole peek into its interior and discover the quantum gravity secrets locked up in the hole’s central singularity (Chapter 13 ).
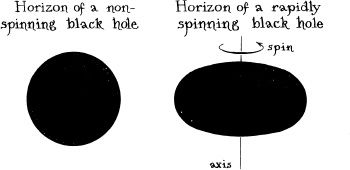
7.9 The shapes of the horizons of two black holes, one ( left) not spinning, and the other (right) spinning with a spin rate 58 percent of the maximum. The effect of the spin on the horizon shape was discovered in 1973 by Larry Smarr, a student at Stanford University who was inspired by Wheeler.
For a hole with the mass of the Sun, the maximum spin rate is one revolution each 0.000062 second (62 microseconds). Since the hole’s circumference is about 18.5 kilometers, this corresponds to a spin speed of about (18.5 kilometers)/(0.000062 second), which is about the speed of light, 299,792 kilometers per second (not entirely a coincidence!). A hole whose mass is 1 million Suns has a 1 million times larger circumference than a l-solar-mass hole, so its maximum spin rate (the rate which makes it spin at about the speed of light) is 1 million times smaller, one revolution each 62 seconds.
I n 1969, Roger Penrose (about whom we shall learn much in Chapter 13 ) made a marvelous discovery. By manipulating the equations of Kerr’s solution to the Einstein field equation, he discovered that a spinning black hole stores rotational energy in the swirl of space around itself, and because the swirl’s energy is outside the hole’s horizon and not inside, this energy can actually be extracted and used to power things. Penrose’s discovery was marvelous because (as Demetrios Christodoulou later showed) the hole’s rotational energy is huge. If the hole spins at its maximum possible rate, its efficiency at storing and releasing energy is 48 times higher than the efficiency of all the Sun’s nuclear fuel. If it were to burn all its nuclear fuel (actually, it will not burn all), the Sun would only be able to convert a fraction 0.006 of its mass into heat and light. If one were to extract all of a fast-spinning hole’s rotational energy (thereby halting its spin), one would get out 48 × 0.006 = 29 percent of the hole’s mass as usable energy.
Amazingly, physicists had to search for seven years before they discovered a practical method by which nature might extract a hole’s spin energy and put it to use. Their search led the physicists through one crazy method after another, all of which would work in principle but none of which showed much practical promise, before they finally discovered nature’s cleverness. In Chapter 9 I shall describe this search and discovery, and its payoff: a black-hole “machine” for powering quasars and gigantic jets.
I f, as we have seen, electric charge produces electric field lines that stick radially out of a hole’s horizon, and spin produces a swirl in space around the hole, a distortion of the horizon’s shape, and a storage of energy, then what happens when a hole has both charge and spin? Unfortunately, the answer is not terribly interesting; it contains little new. The hole’s charge produces the usual electric field lines. The hole’s spin creates the usual swirl of the hole’s space, it stores the usual rotational energy, and it makes the horizon’s equator bulge out in the usual manner. The only things new are a few rather uninteresting magnetic field lines, created by the swirl of space as it flows through the electric field. (These field lines are not a new form of “hair” on the hole; they are merely a manifestation of the interaction of the old, standard forms of hair: the interaction of the spin-induced swirl with the charge-induced electric field.) All the properties of a spinning, charged black hole are embodied in an elegant solution to the Einstein field equation derived in 1965 by Ted Newman at the University of Pittsburgh and a bevy of his students: Eugene Couch, K. Chinnapared, Albert Exton, A. Prakash, and Robert Torrence.
N ot only can black holes spin; they can also pulsate. Their pulsations, however, were not discovered mathematically until nearly a decade after their spin; the discovery was impeded by a powerful mental block.
For three years (1969–71) John Wheeler’s progeny “watched” black holes pulsate, and didn’t know what they were seeing. The progeny were Richard Price (my student, and thus Wheeler’s intellectual grandson), C. V. Vishveshwara and Lester Edelstein (students of Charles Misner’s at the University of Maryland, and thus also Wheeler’s intellectual grandsons), and Frank Zerilli (Wheeler’s own student at Princeton). Vishveshwara, Edelstein, Price, and Zerilli watched black holes pulsate in computer simulations and in pencil-and-paper calculations. What they thought they were seeing was gravitational radiation (ripples of spacetime curvature) bouncing around in the vicinity of a hole, trapped there by the hole’s own spacetime curvature. The trapping was not complete; the ripples would gradually leak out of the hole’s vicinity, and fly away. This was sort of cute, but not terribly interesting.
In autumn 1971, Bill Press, a new graduate student in my group, realized that the ripples of spacetime curvature bouncing around near a hole could be thought of as pulsations of the black hole itself. After all, as seen from outside its horizon, the hole consists of nothing but space-time curvature. The ripples of curvature were thus nothing more nor less than pulsations of the hole’s curvature, and therefore pulsations of the hole itself.
This change of viewpoint had a huge impact. If we think of black holes as able to pulsate, then it is natural to ask whether there are any similarities between their pulsations and the pulsations (“ringing”) of a bell, or the pulsations of a star. Before Press’s insight, such questions weren’t asked. Afterwards, such questions were obvious.
A bell and a star have natural frequencies at which they like to pulsate. (The bell’s natural frequencies produce its pure ringing tone.) Are there similarly natural frequencies at which a black hole likes to pulsate? Yes, Press discovered, using computer simulations. This discovery triggered Chandrasekhar, together with Steven Detweiler (an intellectual great-grandson of Wheeler’s), to embark on a project of cataloging all of a black hole’s natural frequencies of pulsation. We shall return to those frequencies, the bell-like tones of a black hole, in Chapter 10 .
When a rapidly spinning automobile wheel is slightly out of alignment, it can begin to vibrate, and its vibrations can begin to extract energy from the spin and use that energy to grow stronger and stronger. The vibrations can grow so strong, in fact, that in extreme cases they can even tear the wheel off the car. Physicists describe this by the phrase “the wheel’s vibrations are unstable.” Bill Press was aware of this and of an analogous behavior of spinning stars, so it was natural for him to ask, when he discovered that black holes can pulsate, “If a black hole spins rapidly, will its pulsations be unstable? Will they extract energy from the hole’s spin and use that energy to grow stronger and stronger, and can the pulsations grow so strong that they tear the hole apart?” Chandrasekhar (who was not yet deeply immersed in black-hole research) thought yes. I thought no. In November 1971, we made a bet.
The tools did not yet exist for resolving the bet. What kinds of tools were needed? Since the pulsations would begin weak and only gradually grow strong (if they grew at all), they could be regarded as small “perturbations” of the hole’s spacetime curvature—just as the vibrations of a ringing wine glass are small perturbations of the glass’s shape. This meant that the hole’s pulsations could be analyzed using the perturbation methods whose spirit was described in Box 7.1 above. However, the specific perturbation methods which Price, Press, Vish-veshwara, Chandrasekhar, and others were using in the autumn of 1971 would work only for perturbations of nonspinning, or very slowly spinning, black holes. What they needed were entirely new perturbation methods, methods for perturbations of rapidly spinning holes.
The effort to devise such perturbation methods became a hot topic in 1971 and 1972. My students, Misner’s students, Wheeler’s students, and Chandrasekhar with his student John Friedman all worked on it, as did others. The competition was stiff. The winner was Saul Teu-kolsky, a student of mine from South Africa.
Teukolsky recalls vividly the scene when the equations of his method fell into place. “Sometimes when you play with mathematics, your mind starts picking out patterns,” he says. “I was sitting at the kitchen table in our apartment in Pasadena one May evening in 1972, playing with the mathematics; and my wife Roz was making crepes in a Teflon pan, which was supposed not to stick. The crepes kept sticking. Everytime she poured the batter in she would bang the pan on the countertop. She was cursing and banging, and 1 was yelling at her to be quiet because 1 was getting excited; the mathematical terms were starting to cancel each other in my formulas. Everything was canceling! The equations were falling into place! As I sat there staring at my amazingly simple equations, I was filled with this feeling of how dumb I had been; I could have done it six months earlier; all I had to do was collect the right terms together.”

A party at Mama Kovacs’s home in New York City, December 1972. Left to right: Kip Thorne, Margaret Press, Bill Press, Roselyn Teukolsky, and Saul Teukolsky . [Courtesy Sándor J. Kovács.]
Using Teukolsky’s equations, one could analyze all sorts of problems: the natural frequencies of black-hole pulsations, the stability of a hole’s pulsations, the gravitational radiation produced when a neutron star gets swallowed by a black hole, and more. Such analyses, and extensions of Teukolsky’s methods, were immediately undertaken by a small army of researchers: Alexi Starobinsky (a student of Zel’dovich’s), Bob Wald (a student of Wheeler’s), Jeff Cohen (a student of Dieter Brill’s, who was a student of Wheeler’s), and many others. Teukolsky himself, with Bill Press, commanded the most important problem: the stability of black-hole pulsations.
Their conclusion, derived by a mixture of computer calculations and calculations with formulas, was disappointing: No matter how fast a black hole spins, its pulsations are stable. 6 The hole’s pulsations do extract rotational energy from the hole, but they also radiate energy away as gravitational waves; and the rate at which they radiate energy is always greater than the rate they extract it from the hole’s spin. Their pulsational energy thus always dies out. It never grows, and the hole therefore cannot be destroyed by its, pulsations.
Chandrasekhar, dissatisfied with this Press—Teukolsky conclusion because of its crucial reliance on computer calculations, refused to concede our bet. Only when the entire proof could be done directly with formulas would he be fully convinced. Fifteen years later Bernard Whiting, a former postdoc of Hawking’s (and thus an intellectual grandson of Sciama’s), gave such a proof, and Chandrasekhar threw in the towe1. 7
C handrasekhar is even more of a perfectionist than 1. He and Zel’-dovich are at opposite ends of the perfectionist spectrum. So in 1975, when the youths of the golden age declared the golden age finished and exited from black-hole research en masse, Chandrasekhar was annoyed. These youths had carried Teukolsky’s perturbation methods far enough to prove that black holes are probably stable, but they had not brought the methods into a form where other physicists could automatically compute all details of any desired black-hole perturbation—be it a pulsation, the gravitational waves from an infalling neutron star, a black-hole bomb, or whatever. This incompleteness was rankling.
Thus Chandrasekhar, in 1975 at age sixty-five, turned the full force of his mathematical prowess onto Teukolsky’s equations. With unfailing energy and mathematical insight, he drove forward, through the complex mathematics, organizing it into a form that has been characterized as “rococo: splendorous, joyful, and immensely ornate.” Finally in 1983, at age seventy-three, he completed his task and published a treatise entitled The Mathematical Theory of Black Holes —a treatise that will be a mathematical handbook for black-hole researchers for decades to come, a handbook from which they can extract methods for solving any black-hole perturbation problem that catches their fancy.
1. As Saul Teukolsky, a compatriot of Bill Press’s, recalls it, “This conference was Bill’s response to what he considered a provocation. There was another conference going on, to which none of us had been invited. But all the gray eminences were attending, so Bill decided to have a conference only for young people.”
2. In the late 1980s, at my mother’s suggestion, the entire family requested excommunication from the Mormon Church in response to the Church’s suppression of the rights of women.
3. This idea, while correct, has not yet produced any big payoffs, so I shall not discuss it in this book.
4. I have seen it unleashed in public only once. In 1971, on the occasion of his sixtieth birthday, Wheeler happened to be at an elegant banquet in a castle in Copenhagen—a banquet in honor of an international conference, not in honor of him. To celebrate his birthday, Wheeler set off a string of firecrackers behind his banquet chair, creating chaos amongst the nearby diners.
5. In the late 1980s it became clear that the laws of quantum mechanics can give rise to additional conserved quantities, associated with “quantum fields” (a type of field discussed in Chapter 12 ); and since these quantities, like a hole’s mass, spin, and electric charge, cannot be radiated, they will remain as “quantum hair” when a black hole is born. Although this quantum hair might strongly influence the final fate of a microscopic, evaporating black hole ( Chapter 12 ), it is of no consequence for the macroscopic holes (holes weighing more than the Sun) of this and the next few chapters, since quantum mechanics is generally unimportant on macroscopic scales.
6. A significant, mathematical piece of the proof of stability was provided, independently, by Steven Detweiler and James Ipser at Chicago, and a missing piece of the proof was supplied a year later by James Hartle and Dan Wilkins at the University of California at Santa Barbara.
7. Chandrasekhar was supposed to give me a subscription to Playboy as my reward, but my feminist mother and sisters made me feel so guilty that I requested instead a subscription to The Listener
![]()
in which a method to search
for black holes in the sky
is proposed and pursued
and succeeds (probably)
The Method
I magine yourself as J. Robert Oppenheimer. It is 1939; you have just convinced yourself that massive stars, when they die, must form black holes (Chapters 5 and 6 ). Do you now sit down with astronomers and plan a search of the sky for evidence that black holes truly exist? No, not at all. If you are Oppenheimer, then your interests are in fundamental physics; you may offer your ideas to astronomers, but your own attention is now fixed on the atomic nucleus—and on the outbreak of World War 11, which soon will embroil you in the development of the atomic bomb. And what of the astronomers; do they take up your idea? No, not at all. There is a conservatism abroad in the astronomical community, except for that “wild man” Zwicky, pushing his neutron stars (Chapter 5 ). The worldview that rejected Chandrasekhar’s maximum mass for a white-dwarf star (Chapter 4 ) still holds sway.
Imagine yourself as John Archibald Wheeler. It is 1962; you are beginning to be convinced, after mighty resistance, that some massive stars must create black holes when they die (Chapters 6 and 7 ). Do you now sit down with astronomers and plan a search for them? No, not at all. If you are Wheeler, then your interest is riveted on the fiery marriage of general relativity with quantum mechanics, a marriage that may take place at the center of a black hole (Chapter 13 ). You are preaching to physicists that the endpoint of stellar implosion is a great crisis, from which deep new understanding may emerge. You are not preaching to astronomers that they should search for black holes, or even neutron stars. Of searches for black holes you say nothing; of the more promising idea to search for a neutron star, you echo in your writings the conservative view of the astronomical community: “Such an object will have a diameter of the order of 30 kilometers. . . . it will cool rapidly. . . . There is about as little hope of seeing such a faint object as there is of seeing a planet belonging to another star” (in other words, no hope at all).
Imagine yourself as Yakov Borisovich Zel’dovich. It is 1964; Mikhail Podurets, a member of your old hydrogen bomb design team, has just finished his computer simulations of stellar implosion including the effects of pressure, shock waves, heat, radiation, and mass ejection (Chapter 6 ). The simulations produced a black hole (or, rather, a computer’s version of one). You are now fully convinced that some massive stars, when they die, must form black holes. Do you next sit down with astronomers and plan a search for them? Yes, by all means. If you are Zel’dovich, then you have little sympathy for Wheeler’s obsession with the endpoint of stellar implosion. The endpoint will be hidden by the hole’s horizon; it will be invisible. By contrast, the horizon itself and the hole’s influence on its surroundings might well be observable; you just need to be clever enough to figure out how. Understanding the observable part of the Universe is your obsession, if you are Zel’dovich; how could you possibly resist the challenge of searching for black holes?
Where should your search begin? Clearly, you should begin in our own Milky Way galaxy—our disk-shaped assemblage of 10 12 stars. The other big galaxy nearest to our own, Andromeda, is 2 million light-years away, 20 times farther than the size of the Milky Way; see Figure 8.1. Thus, any star or gas cloud or other object in Andromeda will appear 20 times smaller and 400 times dimmer than a similar one in the Milky Way. Therefore, if black holes are hard to detect in the Milky Way, they will be 400 times harder to detect in Andromeda—and enormously harder still in the 1 billion or so large galaxies beyond Andromeda.
8.1 A sketch of the structure of our Universe.
If searching nearby is so important, then why not search in our own solar system, the realm stretching from the Sun out to the planet Pluto? Might there be a black hole here, among the planets, unnoticed because of its darkness? No, clearly not. The gravitational pull of such a hole would be greater than that of the Sun; it would totally disrupt the orbits of the planets; no such disruption is seen. The nearest hole, therefore, must be far beyond the orbit of Pluto.
How far beyond Pluto? You can make a rough estimate. If black holes are formed by the deaths of massive stars, then the nearest hole is not likely to be much closer than the closest massive star, Sirius, at 8 light-years from Earth; and it almost certainly won’t be closer than the closest of all stars (aside from the Sun), Alpha Centauri, at 4 light-years distance.
How could an astronomer possibly detect a black hole at such a great distance? Could an astronomer just watch the sky for a moving, dark object which blots out the light from stars behind it? No. With its circumference of roughly 50 kilometers and its distance of at least 4 light-years, the hole’s dark disk will subtend an angle no larger than 10 −7 arc second. That is roughly the thickness of a human hair as seen from the distance of the Moon, and 10 million times smaller than the resolution of the world’s best telescopes. The moving dark object would be invisibly tiny.
If one could not see the hole’s dark disk as the hole goes in front of a star, might one see the hole’s gravity act like a lens to magnify the star’s light (Figure 8.2) ? Might the star appear dim at first, then brighten as the hole moves between Earth and the star, then dim again as the hole moves on? No, this method of search also will fail. The reason it will fail depends on whether the star and the hole are orbiting around each other and thus are close together, or are separated by typical interstellar distances. If they are close together, then the tiny hole will be like a hand-held magnifying glass placed upright on a windowsill on the eighty-ninth floor of the Empire State Building, and then viewed from several kilometers distance. Of course, the tiny magnifying glass has no power to magnify the building’s appearance, and similarly the hole has no effect on the star’s appearance.
8.2 A black hole’s gravity should act like a lens to change the apparent size and shape of a star as seen from Earth. In this figure the hole is precisely on the line between the star and the Earth, so light rays from the star can reach the Earth equally well by going over the top of the hole, or under the bottom, or around the front, or around the back. All the light rays reaching Earth move outward from the star on a diverging cone; as they pass the hole they get bent down toward Earth; they then arrive at Earth on a converging cone. The resulting image of the star on the Earth’s sky is a thin ring. This ring has far larger surface area, and hence far larger total brightness, than the star’s image would have if the black hole were absent. The ring is too small to be resolved by a telescope, but the star’s total brightness can be increased by a factor of 10 or 100 or more.
If the star and the hole are far apart as in Figure 8.2, however, the strength of the focusing can be large, an increase of 10 or 100 or more in stellar brightness. But interstellar distances are so vast that the necessary Earth–hole–star lineup would be an exceedingly rare event, so rare that to search for one would be hopeless. Moreover, even if such a lensing were observed, the light rays from star to Earth would pass the hole at so large a distance (Figure 8.2) that there would be room for an entire star to sit at the hole’s location and act as the lens. An astronomer on Earth thus could not know whether the lens was a black hole or merely an ordinary, but dim, star.
Zel’dovich must have gone through a chain of reasoning much like this as he sought a method to observe black holes. His chain led finally to a method with some promise (Figure 8.3): Suppose that a black hole and a star are in orbit around each other (they form a binary system). When astronomers train their telescopes on this binary, they will see light from only the star; the hole will be invisible. However, the star’s light will give evidence of the hole’s presence: As the star moves around the hole in its orbit, it will travel first toward the Earth and then away. When it is traveling toward us, the Doppler effect should shift the star’s light toward the blue, and when moving away, toward the red. Astronomers can measure such shifts with high precision, since the star’s light, when sent through a spectrograph (a sophisticated form of prism), exhibits sharp spectral lines, and a slight change in the wavelength (color) of such a line stands out clearly. From a measurement of the shift in wavelength, astronomers can infer the velocity of the star toward or away from Earth, and by monitoring the shift as time passes, they can infer how the star’s velocity changes with time. The magnitude of those changes might typically be somewhere between 10 and 100 kilometers per second, and the accuracy of the measurements is typically 0.1 kilometer per second.
What does one learn from such high-precision measurements of the star’s velocity? One learns something about the mass of the hole: The more massive is the hole, the stronger is its gravitational pull on the star, and thus the stronger must be the centrifugal forces by which the star resists getting pulled into the hole. To acquire strong centrifugal forces, the star must move rapidly in its orbit. Thus, large orbital velocity goes hand in hand with large black-hole mass.
To search for a black hole, then, astronomers should look for a star whose spectra show a telltale periodic shift from red to blue to red to blue. Such a shift is an unequivocal sign that the star has a companion. The astronomers should measure the star’s spectra to infer the velocity of the star around its companion, and from that velocity they should infer the companion’s mass. If the companion is very massive and no light is seen from it at all, then the companion might well be a black hole. This was Zel’dovich’s proposal.
8.3 Zel’dovich’s proposed method of searching for a black hole. (a) The hole and a star are in orbit around each other. If the hole is heavier than the star, then its orbit is smaller than the star’s as shown (that is, the hole moves only a little while the star moves a lot). If the hole were lighter than the star, then its orbit would be the larger one (that is, the star would move only a little while the hole moves a lot). When the star is moving away from Earth, as shown, its light is shifted toward the red (toward longer wavelength). (b) The light, upon entering a telescope on Earth, is sent through a spectrograph to form a spectrum. Here are shown two spectra, the top recorded when the star is moving away from Earth, the bottom a half orbit later when the star is moving toward Earth. The wavelengths of the sharp lines in the spectra are shifted relative to each other. (c) By measuring a sequence of such spectra, astronomers can determine how the velocity of the star toward and away from the Earth changes with time, and from that changing velocity, they can determine the mass of the object around which the star orbits. If the mass is larger than about 2 Suns and no light is seen from the object, then the object might be a black hole.
Although this method was vastly superior to any previous one, it nevertheless is fraught with many pitfalls, of which I shall discuss just two: First, the weighing of the dark companion is not straightforward. The star’s measured velocity depends not only on the companion’s mass, but also on the mass of the star itself, and on the inclination of the binary’s orbital plane to our line of sight. While the star’s mass and the inclination may be inferred from careful observations, one cannot do so with ease or with good accuracy. As a result, one can readily make large errors (say, a factor of 2 or 3) in one’s estimate of the mass of the dark companion. Second, black holes are not the only kind of dark companions that a star might have. For example, a neutron-star companion would also be dark. To be certain the companion is not a neutron star, one needs to be very confident that it is much heavier than the maximum allowed for a neutron star, about 2 solar masses. Two neutron stars in a tight orbit around each other could also be dark and could weigh as much as 4 Suns. The dark companion might be such a system; or it might be two cold white dwarfs in a tight orbit with total mass as much as 3 Suns. And there are other kinds of stars that, while not completely dark, can be rather massive and abnormally dim. One must look very carefully at the measured spectra to be certain there is no sign of tiny amounts of light from such stars.
Astronomers had worked hard over the preceding decades to observe and catalog binary star systems, so it was not necessary for Zel’dovich to conduct his search directly in the sky; he could search the astronomers’ catalogs instead. However, he had neither the time nor the patience to comb through the catalogs himself, nor did he have the expertise to avoid all the pitfalls. Therefore, as was his custom in such a situation, he commandeered the time and the talents of someone else—in this case, Oktay Guseinov, an astronomy graduate student who already knew much about binary stars. Together, Guseinov and Zel’dovich found five promising black-hole candidates among the many hundreds of well-documented binary systems in the catalogs.
Over the next few years, astronomers paid little attention to these five black-hole candidates. I was rather annoyed at the astronomers’ lack of interest, so in 1968 I enlisted Virginia Trimble, a Caltech astronomer, to help me revise and extend the Zel’dovich-Guseinov list. Trimble, though only months past her Ph.D., had already acquired a formidable knowledge of the lore of astronomy. She knew all the pitfalls we might encounter—those described above and many more—and she could gauge them accurately. By searching through the catalogs ourselves, and by collating all the published data we could find on the most promising binaries, we came up with a new list of eight black-hole candidates. Unfortunately, in all eight cases, Trimble could invent a semi-reasonable non–black-hole explanation for why the companion was so dark. Today, a quarter century later, none of our candidates has survived. It now seems likely that none of them is truly a black hole.
Z el’dovich knew, when he conceived it, that this binary star method of search was a gamble, by no means assured of success. Fortunately, his brainstorming on how to search for black holes produced a second idea—an idea conceived simultaneously and independently, in 1964, by Edwin Salpeter, an astrophysicist at Cornell University in Ithaca, New York.
Suppose that a black hole is traveling through a cloud of gas—or, equivalently, as seen by the hole a gas cloud is traveling past it (Figure 8.4). Then streams of gas, accelerated to near the speed of light by the hole’s gravity, will fly around opposite sides of the hole and come crashing together at the hole’s rear. The crash, in the form of a shock front (a sudden, large increase in density), will convert the gas’s huge energy of infall into heat, causing it to radiate strongly. In effect, then, the black hole will serve as a machine for converting some of the mass of infalling gas into heat and then radiation. This “machine” could be highly efficient, Zel’dovich and Salpeter deduced—far more efficient, for example, than the burning of nuclear fuel.
8.4 The Salpeter–Zel’dovich proposal for how to detect a black hole.
Zel’dovich and his team mulled over this idea for two years, looking at it first from this direction and then that, searching for ways to make it more promising. However, it was but one of dozens of ideas about black holes, neutron stars, supernovae, and the origin of the Universe that they were pursuing, and it got only a little attention. Then, one day in 1966, in an intense discussion, Zel’dovich and Novikov together realized they could combine the binary star idea with the infalling gas idea (Figure 8.5).
Strong winds of gas (mostly hydrogen and helium) blow off the surfaces of some stars. (The Sun emits such a wind, though only a weak one.) Suppose that a black hole and a wind-emitting star are in orbit around each other. The hole will capture some of the wind’s gas, heat it in a shock front, and force it to radiate. At the one-meter-square black-board in Zel’dovich’s Moscow apartment, he and Novikov estimated the temperature of the shocked gas: several million degrees.

8.5 The Zel’dovich-Novikov proposal of how to search for a black hole. A wind, blowing off the surface of a companion star, is captured by the hole’s gravity. The wind’s streams of gas swing around the hole in opposite directions and collide in a sharp shock front, where they are heated to millions of degrees temperature and emit X-rays. Optical telescopes should see the star orbiting around a heavy, dark companion. X-ray telescopes should see X-rays from the companion.
Gas at such a temperature does not emit much light. It emits X-rays instead. Thus, Zel’dovich and Novikov realized, among those black holes which orbit around stellar companions, a few (though not most) might shine brightly with X-rays.
To search for black holes, then, one could use a combination of optical telescopes and X-ray telescopes. The black-hole candidates would be binaries in which one object is an optically bright but X-ray-dark star, and the other is an optically dark but X-ray-bright object (the black hole). Since a neutron star could also capture gas from a companion, heat it in shock fronts, and produce X-rays, the weighing of the optically dark but X-ray-bright object would be crucial. One must be sure it is heavier than 2 Suns and thus not a neutron star.
There was but one problem with this search strategy. In 1966, X-ray telescopes were extremely primitive.
The Search
T he trouble with X-rays, if you are an astronomer, is that they cannot penetrate the Earth’s atmosphere. (If you are a human, that is a virtue, since X-rays cause cancer and mutations.)
Fortunately, experimental physicists with vision, led by Herbert Friedman of the D.S. Naval Research Laboratory (NRL), had been working since the 1940s to lay the groundwork for space-based X-ray astronomy. Friedman and his colleagues had begun, soon after World War 11, by flying instruments to study the Sun on captured German V-2 rockets. Friedman has described their first flight, on 28 June 1946, which carried in the rocket’s nose a spectrograph for studying the Sun’s far ultraviolet radiation. (Far ultraviolet rays, like X-rays, cannot penetrate the Earth’s atmosphere.) After soaring above the atmosphere briefly and collecting data, “the rocket returned to Earth, nose down, in streamlined flight and buried itself in an enormous crater some 80 feet in diameter and 30 feet deep. Several weeks of digging recovered just a small heap of unidentifiable debris; it was as if the rocket had vaporized on impact.”
From this inauspicious beginning, the inventiveness, persistence, and hard work of Friedman and others brought ultraviolet and X-ray astronomy step by step to fruition. By 1949 Friedman and his colleagues were flying Geiger counters on V-2 rockets to study X-rays from the Sun. By the late 1950s, now flying their counters on American-made Aerobee rockets, Friedman and colleagues were studying ultraviolet radiation not only from the Sun, but also from stars. X-rays, however, were another matter. Each second the Sun dumped 1 million X-rays onto a square centimeter of their Geiger counter, so detecting the Sun with X-rays was relatively easy. Theoretical estimates, however, suggested that the brightest X-ray stars would be 1 billion times fainter than the Sun. To detect so faint a star would require an X-ray detector 10 million times more sensitive than those that Friedman was flying in 1958. Such an improvement was a tall order, but not impossible.
By 1962, the detectors had been improved 10,OOO-fold. With just another factor of a thousand to go, other research groups, impressed by Friedman’s progress, were beginning to compete with him. One, a team led by Riccardo Giacconi, would become a formidable competitor.
In a peculiar way, Zel’dovich may have shared responsibility for Giacconi’s success. In 1961, the Soviet Union unexpectedly abrogated a mutual Soviet/American three-year moratorium on the testing of nuclear weapons, and tested the most powerful bomb ever exploded by humans—a bomb designed by Zel’dovich’s and Sakharov’s teams at the Installation (Chapter 6 ). In panic, the Americans prepared new bomb tests of their own. These would be the first American tests in the era of Earth-orbiting spacecraft. For the first time it would be possible to measure, from space, the X-rays, gamma rays, and high-energy particles emerging from nuclear explosions. Such measurements would be crucial for monitoring future Soviet bomb tests. To make such measurements on the impending series of American tests, however, would require a crash program. The task of organizing and leading it went to Giacconi, a twenty-eight-year-old experimental physicist at American Science and Engineering (a private Cambridge, Massachusetts, company), who had recently begun to design and fly X-ray detectors like Friedman’s. The U.S. Air Force gave Giacconi all the money he needed, but little time. In less than a year, he augmented his six-person X-ray astronomy team by seventy new people, designed, built, and tested a variety of weapons-blast monitoring instruments, and flew them with a 95 percent success rate in twenty-four rockets and six satellites. This experience molded the core members of his group into a loyal, dedicated, and highly skilled team, ideally primed to beat all competitors in the creation of X-ray astronomy.
Left: Herbert Friedman, with payload from an Aerobee rocket, in 1968. Right: Riccardo Giacconi with the Uhuru X-ray detector, ca. 1970. [Left: courtesy U.S. Naval Research Laboratory; right: courtesy R. Giacconi.]
Giacconi’s seasoned team took its first astronomical step with a search for X-rays from the Moon, using a detector patterned after Friedman’s, and like Friedman, flying it on an Aerobee rocket. Their rocket, launched from White Sands, New Mexico, at one minute before midnight on 18 June 1962, climbed quickly to an altitude of 230 kilometers, then fell back to Earth. For 350 seconds it was high enough above the Earth’s atmosphere to detect the Moon’s X-rays. The data, telemetered back to the ground, were puzzling; the X-rays were far stronger than expected. When examined more closely, the data were even more surprising. The X-rays seemed to be coming not from the Moon, but from the constellation Scorpius (Figure 8.6b). For two months, Giacconi and his team members (Herbert Gursky, Frank Paolini, and Bruno Rossi) sought errors in their data and apparatus. When none could be found, they announced their discovery: The first X-ray star ever detected, 5000 times brighter than theoretical astrophysicists had predicted Ten months later, Friedman’s team confirmed the discovery, and the star was given the name Sco X-1 (1 for “the brightest,” X for “X-ray source,” Sco for “in the constellation Scorpius”).
8.6 The improving technology and performance of X-ray astronomy’s tools, 1962–1978. (a) Schematic design of the Geiger counter used by Giacconi’s team in their 1962 discovery of the first X-ray star. (b) The data from that Geiger counter, showing that the star was not at the location of the Moon; note the very poor angular resolution (large error box), 90 degrees. (c) The 1970 Uhuru X-ray detector: A vastly improved Geiger counter sits inside the box, and in front of the counter one sees venetian-blind slats that prevent the counter from detecting an X-ray unless it arrives nearly perpendicular to the counter’s window. (d) Uhuru’s measurements of X-rays from the black-hole candidate Cygnus X-t. (e) Schematic diagram and (I) photograph of the mirrors that focus X-rays in the 1978 X-ray telescope Einstein. (g, h) Photographs made by the Einstein telescope of two black-hole candidates, Cygnus X-1 and SS-433. [Individual drawings and pictures courtesy R. Giacconi.]
How had the theorists gone wrong? How had they underestimated by a factor of 5000 the strengths of cosmic X-rays? They had presumed, wrongly, that the X-ray sky would be dominated by objects already known in the optical sky—objects like the Moon, planets, and ordinary stars that are poor emitters of X-rays. However, Sco X-1 and other X-ray stars soon to be discovered were not a type of object anyone had ever seen before. They were neutron stars and black holes, capturing gas from normal-star companions and heating it to high temperatures in the manner soon to be proposed by Zel’dovich and Novikov (Figure 8.5 above). To deduce that this was indeed the nature of the observed X-ray stars, however, would require another decade of hand-in-hand hard work by experimenters like Friedman and Giacconi and theorists like Zel’dovich and Novikov.
G iacconi’s 1962 detector was exceedingly simple (Figure 8.6a): an electrified chamber of gas, with a thin window in its top face. When an X-ray passed through the window into the chamber, it knocked electrons off some of the gas’s atoms; and those electrons were pulled by an electric field onto a wire, where they created an electric current that announced the X-ray’s arrival. (Such chambers are sometimes called Geiger counters and sometimes proportional counters.) The rocket carrying the chamber was spinning at two rotations per second and its nose slowly swung around from pointing up to pointing down. These motions caused the chamber’s window to sweep out a wide swath of sky, pointing first in one direction and then another. When pointed toward the constellation Scorpius, the chamber recorded many X-ray counts. When pointed elsewhere, it recorded few. However, because X-rays could enter the chamber from a wide range of directions, the chamber’s estimate of the location of Sco X-1 on the sky was highly uncertain. It could report only a best-guess location, and a surrounding 90-degree-wide error box indicating how far wrong the best guess was likely to be (see Figure 8.6b).
To discover that Sco X-1 and other X-ray stars soon to be found were in fact neutron stars and black holes in binary systems would require error boxes (uncertainties in position on the sky) a few minutes of arc in size or smaller. That was a very tall order: a 1000-fold improvement in angular accuracy.
The needed improvement, and much more, came step by step over the next sixteen years, with several teams (Friedman’s, Giacconi’s, and others) competing at each step of the way. A succession of rocket flights by one team after another with continually improving detectors was followed, in December 1970, by the launch of Uhuru, the first X-ray satellite (Figure 8.6c). Built by Giacconi’s team, Uhuru contained a gas-filled, X-ray counting chamber one hundred times larger than the one they flew on their 1962 rocket. In front of the chamber’s window were slats, like venetian blinds, to prevent the chamber from seeing X-rays from any direction except a few degrees around the perpendicular (Figure 8.6d). Uhuru, which discovered and cataloged 339 X-ray stars, was followed by several other similar but special-purpose X-ray satellites, built by American, British, and Dutch scientists. Then in 1978 Giacconi’s team flew a grand successor to Uhuru: Einstein, the world’s first true X-ray telescope. Because X-rays penetrate right through any object that they strike perpendicularly, even a mirror, the Einstein telescope used a set of nested mirrors along which the X-rays slide, like a tobogan sliding down an icy slope (Figures 8.6e,f). These mirrors focused the X-rays to make images of the X-ray sky 1 arc second in size-images as accurate as those made by the world’s best optical telescopes (Figures 8.6g,h).
From Giacconi’s rocket to the Einstein telescope in just sixteen years (1962 to 1978), a 300,000-fold improvement of angular accuracy had been achieved, and in the process our understanding of the Universe had been revolutionized: The X-rays had revealed neutron stars, black-hole candidates, hot diffuse gas that bathes galaxies when they reside in huge clusters, hot gas in the remnants of supernovae and in the coronas (outer atmospheres) of some types of stars, and particles with ultra-high energies in the nuclei of galaxies and quasars.
O f the several black-hole candidates discovered by X-ray detectors and X-ray telescopes, Cygnus X-1 (Cyg X-1 for short) was one of the most believable. In 1974, soon after it became a good candidate, Stephen Hawking and I made a bet; he wagered that it is not a black hole, I that it is.
Carolee Winstein, whom I married a decade after the bet was made, was mortified by the stakes (Penthouse magazine for me if I win; Private Eye magazine for Stephen if he wins). So were my siblings and mother. But they didn’t need to worry that I would actually win the Penthouse subscription (or so I thought in the 1980s); our information about the nature of Cyg X-1 was improving only very slowly. By 1990, in my view, we could be only 95 percent confident it was a black hole, still not confident enough for Stephen to concede. Evidently Stephen read the evidence differently. Late one night in June 1990, while I was in Moscow working on research with Soviet colleagues, Stephen and an entourage of family, nurses, and friends broke into my office at Caltech, found the framed bet, and wrote a concessionary note on it with validation by Stephen’s thumbprint.

Right: The bet between Stephen Hawking and me as to whether Cygnus X-1 is a black hole. Left: Hawking lecturing at the University of Southern California in June 1990, just two hours before breaking into my office and signing off on our bet. [Hawking photo courtesy Irene Fertik, University of Southern California.]
The evidence that Cyg X-l contains a black hole is of just the sort that Zel’dovich and Novikov envisioned when they proposed the method of search: Cyg X-l is a binary made of an optically bright and X-ray-dark star orbiting around an X-ray-bright and optically dark companion, and the companion has been weighed to make sure it is too heavy to be a neutron star and thus is probably a black hole.
The evidence that this is the nature of eyg X-1 was not developed easily. It required a cooperative, massive, worldwide effort carried out in the 1960s and 1970s by hundreds of experimental physicists, theoretical astrophysicists, and observational astronomers.
The experimental physicists were people like Herbert Friedman, Stuart Bowyer, Edward Byram, and Talbot Chubb, who discovered eyg X-1 in a rocket flight in 1964; Harvey Tananbaum, Edwin Kellog, Herbert Gursky, Stephen Murray, Ethan Schrier, and Riccardo Giacconi, who used Uhuru in 1971 to produce a 2-arc-minute-sized error box for the position of Cyg X-1 (Figure 8.7); and many others who discovered and studied violent, chaotic fluctuations of the X-rays and their energies—fluctuations that are what one would expect from hot, turbulent gas around a black hole.
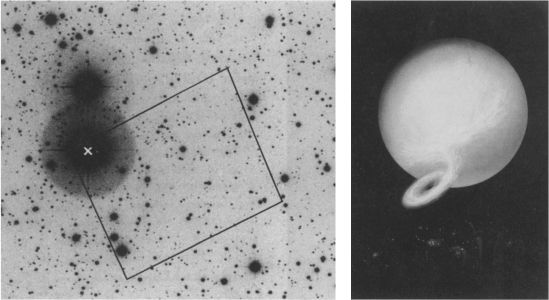
8.7 Left: A negative print of a photograph taken with the 5-meter (200-inch) optical telescope at Palomar Mountain by Jerome Kristian in 1971. The black rectangle outlines the error box in which Uhuru’s 1971 data say that Cygnus X-1 lies. The white x marks the location of a radio flare, measured by radio telescopes, which coincided with a sudden change in the X-rays from Cyg X-1. The x coincides with the optical star HOE 226868, and thus identifies it as a binary companion of Cyg X-1. In 1978 the X-ray telescope Einstein confirmed this identification; see Figure 8.6g. Right: Artist’s conception of Cyg X-1 and HDE 226868, based on all the optical and X-ray data. [Left: photo courtesy Dr. Jerome Kristian, Carnegie Observatories; right: painting by Victor J. Kelley, courtesy the National Geographic Society.]
The observational astronomers contributing to the worldwide effort were people like Robert Hjellming, Cam Wade, Luc Braes, and George Miley, who discovered in 1971 a flare of radio waves in Uhuru’s Cyg X-1 error box simultaneous with a huge, Uhuru-measured change in Cyg X-1’s X-rays, and thereby pinned down the location of Cyg X-1 to within 1 second of arc (Figures 8.6d and 8.7); Louise Webster, Paul Murdin, and Charles Bolton, who discovered with optical telescopes that an optical star, HDE 226868, at the location of the radio flare is orbiting around a massive, optically dark but X-ray-bright companion (Cyg X-1); and a hundred or so other optical astronomers who made painstaking measurements of HDE 226868 and other stars in its vicinity, measurements crucial to avoiding severe pitfalls in estimating the mass of Cyg X-1.
The theoretical astrophysicists contributing to the effort included people like Zel’dovich and Novikov, who proposed the method of search; Bohdan Paczynski, Yoram Avni, and John Bahcall, who developed complex but reliable ways to circumvent the mass-estimate pitfalls; Geoffrey Burbidge and Kevin Prendergast, who realized that the hot, X-ray-emitting gas should form a disk around the hole; and Nikolai Shakura, Rashid Sunyaev, James Pringle, Martin Rees, Jerry Ostriker, and many others, who developed detailed theoretical models of the X-ray-emitting gas and its disk, for comparison with the X-ray observations.
By 1974 this massive effort had led, with roughly 80 percent confidence, to the picture of Cyg X-1 and its companion star HDE 226868 that is shown in an artist’s sketch in the right half of Figure 8.7. It was just the kind of picture that Zel’dovich and Novikov had envisioned, but with far greater detail: The black hole at the center of Cyg X-1 has a mass definitely greater than 3 Suns, probably greater than 7 Suns, and most likely about 16; its optically bright but X-ray-dark companion HDE 226868 has a mass probably greater than 20 Suns and most likely about 33, and it is roughly 20 times larger in radius than the Sun; the distance from the star’s surface to the hole is about 20 solar radii (14 million kilometers); and the binary is about 6000 light-years from Earth. Cyg X-l is the second brightest object in the X-ray sky; HDE 226868, while very bright in comparison with most stars seen by a large telescope, is nevertheless too dim to be seen by the naked eye.
In the two decades since 1974, our confidence in this picture of Cyg X-l has increased from roughly 80 percent to, say, 95 percent. (These are my personal estimates.) Our confidence is not 100 percent because, despite enormous efforts, no unequivocal signature of a black hole has yet been found in Cyg X-l. No signal, in X-rays or light, cries out at astronomers saying unmistakably, “I come from a black hole.” It is still possible to devise other, non-black-hole explanations for all the observations, though those explanations are so contorted that few astronomers take them seriously.
By contrast, some neutron stars, called pulsars, produce an unequivocal “I am a neutron star” cry: Their X-rays, or in some cases radio waves, come in sharp pulses that are very precisely timed. The timing is as precise, in some cases, as the ticking of our best atomic clocks. Those pulses can only be explained as due to beams of radiation shining off a neutron star’s surface and swinging past Earth as the star rotates—the analogue of a rotating light beacon at an airport or in a lighthouse. Why is this the only possible explanation? Such precise timing can come only from the rotation of a massive object with massive inertia and thus massive resistance to erratic forces that would make the timing erratic; of all the massive objects ever conceived by the minds of astrophysicists, only neutron stars and black holes can spin at the enormous rates (hundreds of rotations per second) of some pulsars; and only neutron stars, not black holes, can produce rotating beams, because black holes cannot have “hair.” (Any source of such a beam, attached to the hole’s horizon, would be an example of the type of “hair” that a black hole cannot hang on to. 1
An unequivocal black-hole signature, analogous to a pulsar’s pulses, has been sought by astronomers in Cyg X-1 for twenty years, to no avail. An example of such a signature (suggested in 1972 by Rashid Sunyaev, a member of Zel’dovich’s team) is pulsar-like pulses of radiation produced by a swinging beam that originates in a coherent lump of gas orbiting around the hole. If the lump were close to the hole and held itself together for many orbits until it finally began to plunge into the horizon, then the details of its gradually shifting interval between pulses might provide a clear and unambiguous “I am a black hole” signature. Unfortunately, such a signature has never been seen. There seem to be several reasons: (1) The hot, X-ray-emitting gas moves around the black hole so turbulently and chaotically that coherent lumps may hold themselves together for only one or a few orbits, not many. (2) If a few lumps do manage to hold themselves together for a long time and produce a black-hole signature, the turbulent X-rays from the rest of the turbulent gas evidently bury their signature. (3) If Cyg X-1 is indeed a black hole, then mathematical simulations show that most of the X-rays should come from far outside its horizon—from circumferences roughly 10 times critical or more, where there is much more volume from which X-rays can be emitted than near the horizon. At such large distances from the hole, the gravitational predictions of general relativity and Newton’s theory of gravity are approximately the same, so if there were pulses from orbiting lumps, they would not carry a strongly definitive black-hole signature.
For reasons similar to these, astronomers might never find any kind of definitive black-hole signature in any electromagnetic waves produced from the vicinity of a black hole. Fortunately, the prospects are excellent for a completely different kind of black-hole signature: one carried by gravitational radiation. To this we shall return in Chapter 10 .
![]()
T he golden age of theoretical black-hole research (Chapter 7 ) coincided with the observational search for black holes and the discovery of Cyg X-1 and deciphering of its nature. Thus, one might have expected the youths who dominated the golden age (Penrose, Hawking, Novikov, Carter, Israel, Price, Teukolsky, Press, and others) to play key roles in the black-hole search. Not so, except for Novikov. The talents and knowledge that those youths had developed, and the remarkable discoveries they were making about black-hole spin, pulsation, and hairlessness, were irrelevant to the search and to deciphering Cyg X-1. It might have been different if Cyg X-1 had had an unequivocal black-hole signature. But there was none.
These youths and other theoretical physicists like them are sometimes called relativists, because they spend so much time working with the laws of general relativity. The theorists who did contribute to the search (Zel’dovich, Paczynski, Sunyaev, Rees, and others) were a very different breed called astrophysicists. For the search, these astrophysicists needed to master only a tiny amount of general relativity—just enough to be confident that curved spacetime was quite irrelevant, and that a Newtonian description of gravity would be quite sufficient for modeling an object like Cyg X-1. However, they needed enormous amounts of other knowledge, knowledge that is part of the standard tool kit of an astrophysicist. They needed a mastery of extensive astronomical lore about binary star systems, and about the structures and evolutions and spectra of the companion stars of black-hole candidates, and about the reddening of starlight by interstellar dust—a key tool in determining the distance to Cyg X-1. They also needed to be experts on such issues as the flow of hot gas, shock waves formed when streams of hot gas collide, turbulence in the gas, frictional forces in the gas caused by turbulence and by chaotic magnetic fields, violent breaking and reconnection of magnetic field lines, the formation of X-rays in hot gas, the propagation of X-rays through the gas, and much much more. Few people could be masters of all this and, simultaneously, be masters of the intricate mathematics of curved spacetime. Human limitations forced a split in the community of researchers. Either you specialized in the theoretical physics of black holes, in deducing from general relativity the properties that black holes ought to have, or you specialized in the astrophysics of binary systems and hot gas falling onto black holes and radiation produced by the gas. You were either a relativist or an astrophysicist
Some of us tried to be both, with only modest success. Zel’dovich, the consummate astrophysicist, had occasional new insights about the fundamentals of black holes. I, as a somewhat talented relativist, tried to build general relativistic models of flowing gas near the black hole in Cyg X-1 But Zel’dovich didn’t understand relativity deeply, and I didn’t understand the astronomical lore very well. The barrier to cross over was enormous. Of all the researchers I knew in the golden age, only Novikov and Chandrasekhar had one foot firmly planted in astrophysics and the other in relativity.
Experimental physicists like Giacconi, who designed and flew X-ray detectors and satellites, faced a similar barrier. But there was a difference. Relativists were not needed in the search for black holes, whereas experimental physicists were essential. The observational astronomers and the astrophysicists, with their mastery of the tools for understanding binaries, gas flow, and X-ray propagation, could do nothing until the experimental physicists gave them detailed X-ray data. The experimental physicists often tried to decipher what their own data said about the gas flow and the possible black hole producing it, before turning the data over to the astronomers and astrophysicists, but with only modest success. The astronomers and astrophysicists thanked them very kindly, took the data, and then interpreted them in their own, more sophisticated and reliable ways.
This dependence of the astronomers and astrophysicists on the experimental physicists is but one of many interdependencies that were crucial to success in the search for black holes. Success, in fact, was a product of joint, mutually interdependent efforts by six different communities of people. Each community played an essential role. Relativists deduced, using the laws of general relativity, that black holes must exist. Astrophysicists proposed the method of search and gave crucial guidance at several steps along the way. Observational astronomers identified HDE 226868, the companion of Cyg X-l; they used periodically shifting spectral lines from it to weigh Cyg X-l; and they made extensive other observations to firm up their estimate of its weight. Experimental physicists created the instruments and techniques that made possible the search for X-ray stars, and they carried out the search that identified Cyg X-l. Engineers and managers at NASA created the rockets and spacecraft that carried the X-ray detectors into Earth orbit. And, not least in importance, American taxpayers provided the funds, several hundreds of millions of dollars, for the rockets, spacecraft, X-ray detectors and X-ray telescopes, and the salaries of the engineers, managers, and scientists who worked with them.
Thanks to this remarkable teamwork, we now, in the 1990s, are almost 100 percent sure that black holes exist not only in Cyg X-l, but also in a number of other binaries in our galaxy.
1. Chapter 7 . The electric field hair of a charged black hole is evenly distributed around the hole’s spin axis and thus cannot produce a concentrated beam.
![]()
in which astronomers are forced to conclude,
without any prior predictions,
that black holes a millionfold heavier than the Sun
inhabit the cores of galaxies (probably)
Radio Galaxies
I f, in 1962 (when theoretical physicists were just beginning to accept the concept of a black hole), anyone had asserted that the Universe contains gigantic black holes, millions or billions of times heavier than the Sun, astronomers would have laughed. Nevertheless, astronomers unknowingly had been observing such gigantic holes since 1939, using radio waves. Or so we strongly suspect today.
Radio waves are the opposite extreme to X-rays. X-rays are electromagnetic waves with extremely short wavelengths, typically 10,000 times shorter than the wavelength of light (Figure P.2 in the Prologue). Radio waves are also electromagnetic, but they have long wavelengths, typically a few meters from wave crest to wave crest, which is a million times longer than the wavelength of light. X-rays and radio waves are also opposites in terms of wave/particle duality (Box 4.1)—the propensity of electromagnetic waves to behave sometimes like a wave and sometimes like a particle (a photon). X-rays typically behave like high-energy particles (photons) and thus are most easily detected with Geiger counters in which the X-ray photons hit atoms, knocking electrons off them (Chapter 8 ). Radio waves almost always behave like waves of electric and magnetic force, and thus are most easily detected with wire or metal antennas in which the waves’ oscillating electric force pushes electrons up and down, thereby creating oscillating signals in a radio receiver attached to the antenna.
Cosmic radio waves (radio waves coming from outside the Earth) were discovered serendipitously in 1932 by Karl Jansky, a radio engineer at the Bell Telephone Laboratories in Holmdel, New Jersey. Fresh out of college, Jansky had been assigned the task of identifying the noise that plagued telephone calls to Europe. In those days, telephone calls crossed the Atlantic by radio transmission, so Jansky constructed a special radio antenna, made of a long array of metal pipes, to search for sources of radio static (Figure 9.1a). Most of the static, he soon discovered, came from thunderstorms, but when the storms were gone, there remained a faint, hissing static. By 1935 he had identified the source of the hiss; it was coming, mostly, from the central regions of our Milky Way galaxy. When the central regions were overhead, the hiss was strong; when they sank below the horizon, the hiss weakened but did not entirely disappear.
This was an amazing discovery. Anyone who had ever thought about cosmic radio waves had expected the Sun to be the brightest source of radio waves in the sky, just as it is the brightest source of light. After all, the Sun is a billion (10 9 ) times closer to us than most other stars in the Milky Way, so its radio waves ought to be roughly 10 9 × 10 9 = 10 18 times brighter than those from other stars. Since there are only 10 12 stars in our galaxy, the Sun should be brighter than all the others put together by a factor of roughly 10 18 /10 12 = 10 6 (a million). How could this argument fail? How could the radio waves from the distant central regions of the Milky Way be so much brighter than those from the nearby Sun?
As amazing as this mystery might be, it is even more amazing, in retrospect, that astronomers paid almost no attention to the mystery. In fact, despite extensive publicity by the Bell Telephone Company, only two astronomers seem to have taken any interest at all in Jansky’s discovery. It was doomed to near oblivion by the same astronomical conservatism that Chandrasekhar was encountering with his claims that no white dwarf can be heavier than 1.4 Suns (Chapter 4 ).
The two exceptions to this general lack of interest were a graduate student, Jesse Greenstein, and a lecturer, Fred Whipple, in Harvard University’s astronomy department. Greenstein and Whipple, pondering Jansky’s discovery, showed that, if the then-current ideas about how cosmic radio waves might be generated were correct, it was impossible for our Milky Way galaxy to produce radio waves as strong as Jansky was seeing. Despite this apparent impossibility, Greenstein and Whipple believed Jansky’s observations; they were sure the problem lay with astrophysical theory, not with Jansky. But with no hints as to where the theory was going wrong, and since, as Greenstein recalls, “I never met anybody else [in the 1930s] who had any interest in the subject, not one astronomer,” they turned their attention elsewhere.
By 1935 (about the time that Zwicky was inventing the concept of a neutron star; Chapter 5 ), Jansky had learned everything about the galactic hiss that his primitive antenna would allow him to discover. In a quest to learn more, he proposed to Bell Telephone Laboratories the construction of the world’s first real radio telescope: a huge metal bowl, 100 feet (30 meters) in diameter, which would reflect incoming radio waves up to a radio antenna and receiver in much the same way that an optical reflecting telescope reflects light from its mirror up to an eyepiece or a photographic plate. The Bell bureaucracy rejected the proposal; there was no profit in it. Jansky, ever the good employee, acquiesced. He abandoned his study of the sky, and in the shadow of the approach of World War 11, turned his efforts toward radio-wave communication at shorter wavelengths.
S o uninterested were professional scientists in Jansky’s discovery that the only person to build a radio telescope during the next decade was Grote Reber, an eccentric bachelor and ham radio operator in Wheaton, Illinois, call number W9GFZ. Having read of Jansky’s radio hiss in the magazine Popular Astronomy, Reber set out to study its details. Reber had a very poor education in science, but that was unimportant. What mattered was his good training in engineering and his strong practical streak. Using enormous ingenuity and his own modest savings, he designed and constructed with his own hands, in his mother’s backyard, the world’s first radio telescope, a 30-foot (that is, 9-meter)diameter dish (Figure 9.1c); and with it, he made radio maps of the sky (Figure 9.1d). In his maps one can see clearly not only the central region of our Milky Way galaxy, but also two other radio sources, later called Cyg A and Cas A—A for the “brightest radio sources,” Cyg and Cas for “in the constellations Cygnus and Cassiopeia.” Four decades of detective work would ultimately show, with high probability, that Cyg A and many other radio sources discovered in the ensuing years are powered by gigantic black holes.

9.1 (a) Karl Jansky and the antenna with which he discovered, in 1932, cosmic radio waves from our galaxy. (b) Grote Reber, ca 1940. (c) The world’s first radio telescope, constructed by Reber in his mother’s backyard in Wheaton, Illinois. (d) A map of radio waves from the sky constructed by Reber with his backyard radio telescope. [(a) Photo by Bell Telephone Laboratories, courtesy AIP Emilio Segrè Visual Archives; (b) and (c) courtesy Grote Reber; (d) is adapted from Reber (1944).]
The story of this detective work will be the central thread of this chapter. I have chosen to devote a whole chapter to the story for several reasons:
First, this story illustrates a mode of astronomical discovery quite different from that illustrated in Chapter 8 . In Chapter 8 , Zel’dovich and Novikov proposed a concrete method to search for black holes; experimental physicists, astronomers, and astrophysicists implemented that method; and it paid off. In this chapter, gigantic black holes are already being observed by Reber in 1939, long before anyone ever thought to look for them, but it will take forty years for the mounting observational evidence to force astronomers to the conclusion that black holes are what they are seeing.
Second, Chapter 8 illustrated the powers of astrophysicists and relativists; this chapter shows their limitations. The types of black holes discovered in Chapter 8 were predicted to exist a quarter century before anyone ever went searching for them. They were the Oppenheimer–Snyder holes: a few times heavier than the Sun and created by the implosion of heavy stars. The gigantic black holes of this chapter, by contrast, were never predicted to exist by any theorist. They are thousands or millions of times heavier than any star that any astronomer has ever seen in the sky, so they cannot possibly be created by the implosion of such stars. Any theorist predicting these gigantic holes would have tarnished his or her scientific reputation. The discovery of these holes was serendipity in its purest form.
Third, this chapter’s story of discovery will illustrate, even more clearly than Chapter 8 , the complex interactions and interdependencies of four communities of scientists: relativists, astrophysicists, astronomers, and experimental physicists.
Fourth, it will turn out, late in this chapter, that the spin and the rotational energy of gigantic black holes play central roles in explaining the observed radio waves. By contrast, a hole’s spin was of no importance for the observed properties of the modest-sized holes in Chapter 8 .
I n 1940, having made his first radio scans of the sky, Reber carefully wrote up a technical description of his telescope, his measurements, and his map, and mailed it to Subrahmanyan Chandrasekhar, who was now the editor of the Astrophysical Journal at the University of Chicago’s Yerkes Observatory, on the shore of Lake Geneva in Wisconsin. Chandrasekhar circulated Reber’s remarkable manuscript among the Yerkes astronomers. Bemused by the manuscript and skeptical of this completely unknown amateur, several of the astronomers drove down to Wheaton, Illinois, to look at his instrument. They returned, impressed. Chandrasekhar approved the paper for publication.
Jesse Greenstein, who had become an astronomer at Yerkes after completing his Harvard graduate studies, made a number of trips down to Wheaton over the next few years and became a close friend of Reber’s. Greenstein describes Reber as “the ideal American inventor. If he had not been interested in radio astronomy, he would have made a million dollars.”
Enthusiastic about Reber’s research, Greenstein tried, after a few years, to move him to the University of Chicago. “The University didn’t want to spend a dime on radio astronomy,” Greenstein recalls. But Otto Struve, the director of the University’s Yerkes Observatory, agreed to a research appointment provided the money to pay Reber and support his research came from Washington. Reber, however, “was an independent cuss,” Greenstein says. He refused to explain to the bureaucrats in any detail how the money for new telescopes would be spent. The deal fell through.
In the meantime, World War II had ended, and scientists who had done technical work in the war effort were looking for new challenges. Among them were experimental physicists who had developed radar for tracking enemy aircraft during the war. Since radar is nothing but radio waves that are sent out from a radio-telescope-like transmitter, bounce off an airplane, and return back to the transmitter, these experimental physicists were ideally poised to give life to the new field of radio astronomy—and some of them were eager to do so; the technical challenges were great, and the intellectual payoffs promising. Of the many who tried their hand at it, three teams quickly came to dominate the field: Bernard Lovell’s team at Jodrell Bank/Manchester University in England; Martin Ryle’s team at Cambridge University in England; and a team put together by J. L. Pawsey and John Bolton in Australia. In America there was little effort of note; Grote Reber continued his radio astronomy research virtually alone.
Optical astronomers (astronomers who study the sky with light, 1 the only kind of astronomer that existed in those days) paid little attention to the experimental physicists’ feverish activity. They would remain uninterested until radio telescopes could measure a source’s position on the sky accurately enough to determine which light-emitting object was responsible for the radio waves. This would require a 100-fold improvement in resolution over that achieved by Reber, that is, a 100-fold improvement in the accuracy with which the positions, sizes, and shapes of the radio sources were measured.
Such an improvement was a tall order. An optical telescope, or even a naked human eye, can achieve a high resolution with ease, because the waves it works with (light) have very short wavelengths, less than 10 −6 meter. By contrast, human ears cannot distinguish very accurately the direction from which a sound comes because sound waves have wavelengths that are long, roughly a meter. Similarly, radio waves, with their meter-sized wavelengths, give poor resolution—unless the telescope one uses is enormously larger than a meter. Reber’s telescope was only modestly larger; hence, its modest resolution. To achieve a 100-fold improvement in resolution would require a telescope 100 times larger, roughly a kilometer in size, and/or the use of shorter wavelength radio waves, for example, a few centimeters instead of one meter.
The experimental physicists actually achieved this l00-fold improvement in 1949, not by brute force, but by cleverness. The key to their cleverness can be understood by analogy with something very simple and familiar. (This is just an analogy; it in fact is a slight cheat, but it gives an impression of the general idea.) We humans can see the three-dimensionality of the world around us using just two eyes, not more. The left eye sees around an object a little bit on the left side, and the right eye sees around it a bit on the right side. If we turn our heads over on their sides we can see around the top of the object a bit and around the bottom of the object a bit; and if we were to move our eyes farther apart (as in effect is done with the pair of cameras that make 3-D movies with exaggerated three-dimensionality), we would see somewhat farther around the object. However, our three-dimensional vision would not be improved enormously by having a huge number of eyes, covering the entire fronts of our faces. We would see things far more brightly with all those extra eyes (we would have a higher sensitivity), but we would gain only modestly in three-dimensional resolution.
Now a huge, 1-kilometer radio telescope (left half of Figure 9.2) would be somewhat like our face covered with eyes. The telescope would consist of a 1-kilometer-sized bowl covered with metal that reflects and focuses the radio waves up to a wire antenna and radio receiver. If we were to remove the metal everywhere except for a few spots widely scattered over the bowl, it would be like removing most of those extra eyes from our face, and keeping only a few. In both cases, there is a modest loss of resolution, but a large loss of sensitivity. What the experimental physicists wanted most was an improved resolution (they wanted to find out where the radio waves were coming from and what the shapes of the radio sources were), not an improved sensitivity (not an ability to see more, dimmer radio sources-at least not for now). Therefore, they needed only a spotty bowl, not a fully covered bowl.
9.2 The principle of a radio interferometer. Left: In order to achieve good angular resolution, one would like to have a huge, say, l-kilometer, telescope. However, it would be sufficient if only a few spots (solid) on the radio-wave-reflecting bowl are actually covered with metal and reflect. Right: It is not necessary for the radio waves reflected from those spots to be focused to an antenna and radio receiver at the huge bowl’s center. Rather, each spot can focus its waves to its own antenna and receiver, and the resulting radio signals can then be carried by wire from all the receivers to a central receiving station, where they are combined in the same manner as they would have been at the huge telescope’s receiver. The result is a network of small radio telescopes with linked and combined outputs, a radio interferometer.
A practical way to make such a spotty bowl was by constructing a network of small radio telescopes connected by wires to a central radio receiving station (right half of Figure 9.2). Each small telescope was like a spot of metal on the big bowl, the wires carrying each small telescope’s radio signal were like radio beams reflected from the big bowl’s spots, and the central receiving station which combines the signals from the wires was like the big bowl’s antenna and receiver, which combine the beams from the bowl’s spots. Such networks of small telescopes, the centerpieces of the experimental physicists’ efforts, were called radio interferometers, because the principle behind their operation was interferometry: By “interfering” the outputs of the small telescopes with each other in a manner we shall meet in Box 10.3 of Chapter 10 , the central receiving station constructs a radio map or picture of the sky.
T hrough the late 1940s, the 1950s, and into the 1960s, the three teams of experimental physicists (Jodrell Bank, Cambridge, and Australia) competed with each other in building ever larger and more sophisticated radio interferometers, with ever improving resolutions. The first crucial benchmark, the 100-fold improvement necessary to begin to stir an interest among optical astronomers, came in 1949, when John Bolton, Gordon Stanley, and Bruce Slee of the Australian team produced 10-arc-minute-sized error boxes for the positions of a number of radio sources; that is, when they identified 10-arc-minutesized regions on the sky in which the radio sources must lie. (Ten arc minutes is one-third the diameter of the Sun as seen from Earth, and thus much poorer resolution than the human eye can achieve with light, but it is a remarkably good resolution when working with radio waves.) When the error boxes were examined with optical telescopes, some, including Cyg A, showed nothing bright of special note; finer radio resolution would be needed to reveal which of the plethora of optically dim objects in these error boxes might be the true sources of the radio waves. In three of the error boxes, however, there was an unusually bright optical object: one remnant of an ancient supernova, and two distant galaxies.
As difficult as it may have been for astrophysicists to explain the radio waves that Jansky had discovered emanating from our own galaxy, it was even more difficult to understand how distant galaxies could emit such strong radio signals. That some of the brightest radio sources in the sky might be objects so extremely distant was too incredible for belief (though it ultimately would turn out to be true). Therefore, it seemed a good bet (but those who made the bet would lose) that each error box’s radio signals were coming not from the distant galaxy, but rather from one of the plethora of optically dim but nearby stars in the error box. Only better resolution could tell for sure. The experimental physicists pushed forward, and a few optical astronomers began to watch with half an eye, mildly interested.
By summer 1951, Ryle’s team at Cambridge had achieved a further 10-fold improvement of resolution, and Graham Smith, a graduate student of Ryle’s, used it to produce a i-are-minute error box for Cyg A—a box small enough that it could contain only a hundred or so optical objects (objects seen with light). Smith airmailed his best-guess position and its error box to the famous optical astronomer Walter Baade at the Carnegie Institution in Pasadena. (Baade was the man who seventeen years earlier, with Zwicky, had identified supernovae and proposed that neutron stars power them—Chapter 5 .) The Carnegie Institution owned the 2.5-meter (100-inch) optical telescope on Mount Wilson, until recently the world’s largest; Caltech, down the street in Pasadena, had just finished building the larger 5-meter (200-inch) telescope on Palomar Mountain; and the Carnegie and Caltech astronomers shared their telescopes with each other. At his next scheduled observing session on the Palomar 5-meter (Figure 9.3a), Baade photographed the error box on the sky where Smith said Cyg A lies. (This spot on the sky, like most spots, had never before been examined through a large optical telescope.) When Baade developed the photograph, he could hardly believe his eyes. There, in the error box, was an object unlike any ever before seen. It appeared to be two galaxies colliding with each other (center of Figure 9.3d). (We now know, thanks to observations with infrared telescopes in the 1980s, that the galaxy collision was an optical illusion. Cyg A is actually a single galaxy with a band of dust running across its face. The dust absorbs light in just such a way as to make the single galaxy look like two galaxies in collision.) The whole system, central galaxy plus radio source, would later come to be called a radio galaxy.
Astronomers were convinced for two years that the radio waves were being produced by a galactic collision. Then, in 1953, came another surprise. R. C. Jennison and M. K. Das Gupta of Lovell’s Jodrell Bank team studied Cyg A using a new interferometer consisting of two telescopes, one fixed to the ground and the other moving around the countryside on a truck so as to cover, one after another, a number of “spots” on the “bowl” of an imaginary 4-kilometer-square telescope (see left half of Figure 9.2). With this new interferometer (Figures 9.3b, c), they discovered that the Cyg A radio waves were not coming from the “colliding galaxies,” but rather from two giant, roughly rectangular regions of space, about 200,000 light-years in size and 200,000 light-years apart, on opposite sides of the “colliding galaxies.” These radio-emitting regions, or lobes as they are called, are shown as rectangles in Figure 9.3d, together with Baade’s optical photograph of the “colliding galaxies.” Also shown in the figure is a more detailed map of the lobes’ radio emission, constructed sixteen years later using more sophisticated interferometers; this map is shown as thin lined contours that exhibit the brightness of the radio emission in the same way as the contours of a topographic map exhibit the height of the land. These contours confirm the 1953 conclusion that the radio waves come from gigantic lobes of gas on either side of the “colliding galaxies.” How both of these enormous lobes can be powered by a single, gigantic black hole will become a major issue later in this chapter.

9.3 The discovery that Cyg A is a distant radio galaxy: (a) The 5-meter optical telescope used in 1951 by Baade to discover that Cyg A is connected with what appeared to be two colliding galaxies. (b) The radio interferometer at Jodrell Bank used in 1953 by Jennison and Das Gupta to show that the radio waves are coming from two giant lobes outside the colliding galaxies. The interferometer’s two antennas (each an array of wires on a wooden framework) are shown here side by side. In the measurements, one was put on a truck and moved around the countryside, while the other remained behind, at rest on the ground. (c) Jennison and Das Gupta, inspecting the radio data in the control room of their interferometer. (d) The two giant lobes of radio emission (rectangles) as revealed in the 1953 measurements, shown together with Baade’s optical photograph of the “colliding galaxies.” Also shown in (d) is a high-resolution contour map of the lobes’ radio emission (thin solid contours), produced in 1969 by Ryle’s group at Cambridge. [(a) Courtesy Palomar Observatory/California Institute of Technology; (b) and (c) courtesy Nuffield Radio Astronomy Laboratories, University of Manchester; (d) adapted from Mitton and Ryle (1969), Baade and Minkowski (1954), Jennison and Das Gupta (1953).]
T hese discoveries were startling enough to generate, at long last, strong interest among optical astronomers. Jesse Greenstein was no longer the only one paying serious attention.
For Greenstein himself, these discoveries were the final straw. Having failed to push into radio work right after the war, Americans were now bystanders in the greatest revolution to hit astronomy since Galileo invented the optical telescope. The rewards of the revolution were being reaped in Britain and Australia, and not in America.
Greenstein was now a professor at Caltech. He had been brought there from Yerkes to build an astronomy program around the new 5-meter optical telescope, so naturally, he now went to Lee DuBridge, the Caltech president, and urged that Caltech build a radio interferometer to be used hand in hand with the 5-meter in exploring distant galaxies. DuBridge, having been director of the American radar effort during the war, was sympathetic, but cautious. To swing DuBridge into action, Greenstein organized an international conference on the future of radio astronomy in Washington, D.C., on 5 and 6 January 1954.
In Washington, after the representatives from the great British and Australian radio observatories had described their remarkable discoveries, Greenstein posed his question: Must the United States continue as a radio astronomy wasteland? The answer was obvious.
With strong backing from the National Science Foundation, American physicists, engineers, and astronomers embarked on a crash program to construct a National Radio Astronomy Observatory in Greenbank, West Virginia; and DuBridge approved Greenstein’s proposal for a state-of-the-art Caltech radio inteferometer, to be built in Owens Valley, California, just southeast of Yosemite National Park. Since nobody at Caltech had the expertise to build such an instrument, Greenstein lured John Bolton from Australia to spearhead the effort.
Quasars
B y the late 1950s, the Americans were competitive. Radio telescopes at Greenbank were coming into operation, and at Caltech, Tom Mathews, Per Eugen Maltby, and Alan Moffett on the new Owens Valley radio interferometer were working hand in hand with Baade, Greenstein, and others on the Palomar 5-meter optical telescope to discover and study large numbers of radio galaxies.
In 1960 this effort brought another surprise: Tom Mathews at Caltech received word from Henry Palmer that, according to Jodrell Bank measurements, a radio source named 3C48 (the 48th source in the third version of a catalog constructed by Ryle’s group at Cambridge) was extremely small, no more than 1 arc second in diameter (1/2,000 of the angular size of the Sun). So tiny a source would be something quite new. However, Palmer and his Jodrell Bank colleagues could not provide a tight error box for the source’s location. Mathews, in exquisitely beautiful work with Caltech’s new radio interferometer, produced an error box just 5 seconds of arc in size, and gave it to Allan Sandage, an optical astronomer at the Carnegie Institution in Pasadena. On his next observing run on the 5-meter optical telescope, Sandage took a photograph centered on Mathews’s error box and found, to his great surprise, not a galaxy, but a single, blue point of light; it looked like a star. “I took a spectrum the next night and it was the weirdest spectrum I’d ever seen,” Sandage recalls. The wavelengths of the spectral lines were not at all like those of stars or of any hot gas ever manufactured on Earth; they were unlike anything ever before encountered by astronomers or physicists. Sandage could not make any sense at all out of this weird object.
Over the next two years a half-dozen similar objects were discovered by the same route, each as puzzling as 3C48. All the optical astronomers at Caltech and Carnegie began photographing them, taking spectra, struggling to understand their nature. The answer should have been obvious, but it was not. A mental block held sway. These weird objects looked so much like stars that the astronomers kept trying to interpret them as a type of star in our own galaxy that had never before been seen, but the interpretations were horrendously contorted, not really believable.
The mental block was broken by Maarten Schmidt, a thirty-two-year-old Dutch astronomer who had recently joined the Caltech faculty. For months he had struggled to understand a spectrum he had taken of 3C273, one of the weird objects. On 5 February 1963, as he sat in his Caltech office carefully sketching the spectrum for inclusion in a manuscript he was writing, the answer suddenly hit him. The four brightest lines in the spectrum were the four standard “Balmer lines” produced by hydrogen gas—the most famous of all spectral lines, the first lines that college physics students learned about in their courses on quantum mechanics. However, these four lines did not have their usual wavelengths. Each was shifted to the red by 16 percent. 3C273 must be an object containing a massive amount of hydrogen gas and moving away from the Earth at 16 percent of the speed of light—enormously faster than any star that any astronomer had ever seen.
Schmidt flew out into the hall, ran into Greenstein, and excitedly described his discovery. Greenstein turned, headed back to his office, pulled out his spectrum of 3C48, and stared at it for a while. Balmer lines were not present at any redshift; but lines emitted by magnesium, oxygen, and neon were there staring him in the face, and they had a redshift of 37 percent. 3C48 was, at least in part, a massive amount of gas containing magnesium, oxygen, and neon, and moving away from Earth at about 37 percent of the speed of light.
What was producing these high speeds? If, as everyone had thought, these weird objects (which would later be named quasars) were some type of star in our own Milky Way galaxy, then they must have been ejected from somewhere, perhaps the Milky Way’s central nucleus, with enormous force. This was too incredible to believe, and a close examination of the quasars’ spectra made it seem extremely unlikely. The only reasonable alternative, Greenstein and Schmidt argued (correctly), was that these quasars are very far away in our Universe, and move away from Earth at high speed as a result of the Universe’s expansion.

Left: Jesse L. Greenstein with a drawing of the Palomar 5-meter optical telescope, ca. 1955. Right: Maarten Schmidt, with an instrument for measuring spectra made by the 5-meter telescope, ca. 1963. [Courtesy the Archives, California Institute of Technology.]
Recall that the expansion of the Universe is like the expansion of the surface of a balloon that is being blown up. If a number of ants are standing on the balloon’s surface, each ant will see all the other ants move away from him as a result of the balloon’s expansion. The farther away another ant is, the faster the first ant will see it move. Similarly, the farther away a distant object is from Earth, the faster we on Earth will see it move as a result of the Universe’s expansion. In other words, the object’s speed is proportional to its distance. Therefore, from the speeds of 3C273 and 3C48, Schmidt and Greenstein could infer their distances: 2 billion light-years and 4.5 billion light-years, respectively.
These were enormous distances, nearly the largest distances ever yet recorded. This meant that, in order for 3C273 and 3C48 to be as bright as they appear in the 5-meter telescope, they had to radiate enormous amounts of power: 100 times more power than the most luminous galaxies ever seen.
3C273, in fact, was so bright that, along with many other objects near it on the sky, it had been photographed more than 2000 times since 1895 using modest-sized telescopes. Upon learning of Schmidt’s discovery, Harlan Smith of the University of Texas organized a close examination of this treasure trove of photographs, archived largely at Harvard, and discovered that 3C273 had been fluctuating in brightness during the past seventy years. Its light output had changed substantially within periods as short as a month. This means that a large portion of the light from 3C273 must come from a region smaller than the distance light travels in a month, that is, smaller than 1 “light-month.” (If the region were larger, then there would be no way that any force, traveling, of course, at a speed less than or equal to that of light, could make the emitting gas all brighten up or dim out simultaneously to within an accuracy of a month.)
The implications were extremely hard to believe. This weird quasar, this 3C273, was shining 100 times more brightly than the brightest galaxies in the Universe; but whereas galaxies produce their light in regions 100,000 light-years in size, 3C273 produces its light in a region at least a million times smaller in diameter and 10 18 times smaller in volume: just a light-month or less. The light must come from a massive, compact, gaseous object that is heated by an enormously powerful engine. The engine would ultimately turn out to be, with high but not complete confidence, a gigantic black hole, but strong evidence for this was still fifteen years into the future.
I f explaining Jansky’s radio waves from our own Milky Way galaxy was difficult, and explaining the radio waves from distant radio galaxies was even more difficult, then the explanation for radio waves from these superdistant quasars would have to be superdifficult.
The difficulty, it turned out, was an extreme mental block. Jesse Greenstein, Fred Whipple, and all other astronomers of the 1930s and 1940s had presumed that cosmic radio waves, like light from stars, are emitted by the heat-induced jiggling of atoms, molecules, and electrons. Astronomers of the thirties and forties could not conceive of any other way for nature to create the observed radio waves, even though their calculations showed unequivocally that this way can’t work.
Another way, however, had been known to physicists since the early twentieth century: When an electron, traveling at high speed, encounters a magnetic field, the field’s magnetic force twists the electron’s motion into a spiral. The electron is forced to spiral around and around the magnetic field lines (Figure 9.4), and as it spirals, it emits electromagnetic radiation. Physicists in the 1940s began to call this radiation synchrotron radiation, because it is produced by spiraling electrons in the particle accelerators called “synchrotrons” that they were then building. Remarkably, in the 1940s, despite physicists’ considerable interest in synchrotron radiation, astronomers paid no attention to it. The astronomers’ mental block held sway.
9.4 Cosmic radio waves are produced by near-light-speed electrons that spiral around and around in magnetic fields. The magnetic field forces an electron to spiral instead of moving on a straight line, and the electron’s spiraling motion produces the radio waves.
In 1950 Karl Otto Kiepenheuer in Chicago and Vitaly Lazarevich Ginzburg in Moscow (the same Ginzburg who had invented the LiD fuel for the Soviet hydrogen bomb, and who had discovered the first hint that black holes have no hair 2 ) broke the mental block. Building on seminal ideas of Hans Alfven and Nicolai Herlofson, Kiepenheuer and Ginzburg proposed (correctly) that Jansky’s radio waves from our own galaxy are synchrotron radiation produced by near-light-speed electrons spiraling around magnetic field lines that fill interstellar space (Figure 9.4).
A few years later, when the giant radio-emitting lobes of radio galaxies and then quasars were discovered, it was natural (and correct) to conclude that their radio waves were also produced by electrons spiraling around magnetic field lines. From the physical laws governing such spiraling and the properties of the observed radio waves, Geoffrey Burbidge at the University of California in San Diego computed how much energy the lobes’ magnetic field and high-speed electrons must have. His startling answer: In the most extreme cases, the radio-emitting lobes must have about as much magnetic energy and high-speed (kinetic) energy as one would get by converting all the mass of 10 million (10 7 ) Suns into pure energy with 100 percent efficiency.
T hese energy requirements of quasars and radio galaxies were so staggering that they forced astrophysicists, in 1963, to examine all conceivable sources of power in search of an explanation.
Chemical power (the burning of gasoline, oil, coal, or dynamite), which is the basis of human civilization, was clearly inadequate. The chemical efficiency for converting mass into energy is no larger than 1 part in a billion (1 part in 10 9 ). To energize a quasar’s radio-emitting gas would therefore require 10 9 × 10 7 = 10 16 solar masses of chemical fuel—100,000 times more fuel than is contained in our entire Milky Way galaxy. This seemed totally unreasonable.
Nuclear power, the basis of the hydrogen bomb and of the Sun’s heat and light, looked only marginal as a way to energize a quasar. Nuclear fuel’s efficiency for mass-to-energy conversion is roughly 1 percent (1 part in 10 2 ), so a quasar would need 10 2 × 10 7 = 10 9 (1 billion) solar masses of nuclear fuel to energize its radio-emitting lobes. And this 1 billion solar masses would be adequate only if the nuclear fuel were burned completely and the resulting energy were converted completely into magnetic fields and kinetic energy of high-speed electrons. Complete burning and complete energy conversion seemed highly unlikely. Even with carefully contrived machines, humans rarely achieve better than a few percent conversion of fuel energy into useful energy, and nature without careful designs might well do worse. Thus, 10 billion or 100 billion solar masses of nuclear fuel seemed more reasonable. Now, this is less than the mass of a giant galaxy, but not a lot less, and how nature might achieve the conversion of the fuel’s nuclear energy into magnetic and kinetic energy was very unclear. Thus, nuclear fuel was a possibility, but not a likely one.
The annihilation of matter with antimatter 3 could give 100 percent conversion of mass to energy, so 5 million solar masses of antimatter annihilating with 5 million solar masses of matter could satisfy a quasar’s energy needs. However, there is no evidence that any antimatter exists in our Universe, except tiny bits created artifically by humans in particle accelerators and tiny bits created by nature in collisions between matter particles. Moreover, even if so much matter and antimatter were to annihilate in a quasar, their annihilation energy would go into very high energy gamma rays, and not into magnetic energy and electron kinetic energy. Thus, matter/antimatter annihilation appeared to be a very unsatisfactory way to energize a quasar.
One other possibility remained: gravity. The implosion of a normal star to form a neutron star or a black hole might, conceivably, convert 10 percent of the star’s mass into magnetic and kinetic energy—though precisely how was unclear. If it managed to do so, then the implosions of 10 × 10 7 = 10 8 (100 million) normal stars might provide a quasar’s energy, as would the implosion of a single, hypothetical, supermassive star 100 million times heavier than the Sun. [The correct idea, that the gigantic black hole produced by the implosion of such a supermassive star might itself be the engine that powers the quasar, did not occur to anybody in 1963. Black holes were but poorly understood. Wheeler had not yet coined the phrase “black hole” (Chapter 6 ). Salpeter and Zel’dovich had not yet realized that gas falling toward a black hole could heat and radiate with high efficiency (Chapter 8 ). Penrose had not yet discovered that a black hole can store up to 29 percent of its mass as rotational energy, and release it (Chapter 7 ). The golden age of black-hole research had not yet begun.]
The idea that the implosion of a star to form a black hole might energize quasars was a radical departure from tradition. This was the first time in history that astronomers and astrophysicists had felt a need to appeal to effects of general relativity to explain an object that was being observed. Previously, relativists had lived in one world and astronomers and astrophysicists in another, hardly communicating. Their insularity was about to end.
To foster dialogue between the relativists and the astronomers and astrophysicists, and to catalyze progress in the study of quasars, a conference of three hundred scientists was held on 16–18 December 1963, in Dallas, Texas. In an after-dinner speech at this First Texas Symposium on Relativistic Astrophysics, Thomas Gold of Cornell University described the situation, only partially with tongue in cheek: “[The mystery of the quasars] allows one to suggest that the relativists with their sophisticated work are not only magnificent cultural ornaments but might actually be useful to science! Everyone is pleased: the relativists who feel they are being appreciated and are experts in a field they hardly knew existed, the astrophysicists for having enlarged their domain, their empire, by the annexation of another subject—general relativity. It is all very pleasing, so let us all hope that it is right. What a shame it would be if we had to go and dismiss all the relativists again.”
Lectures went on almost continuously from 8:30 in the morning until 6 in the evening with an hour out for lunch, plus 6 P.M. until typically 2 A.M. for informal discussions and arguments. Slipped in among the lectures was a short, ten-minute presentation by a young New Zealander mathematician, Roy Kerr, who was unknown to the other participants. Kerr had just discovered his solution of the Einstein field equation—the solution which, one decade later, would turn out to describe all properties of spinning black holes, including their storage and release of rotational energy (Chapters 7 and 11 ); the solution which, as we shall see below, would ultimately become a foundation for explaining the quasars’ energy. However, in 1963 Kerr’s solution seemed to most scientists only a mathematical curiosity; nobody even knew it described a black hole—though Kerr speculated it might somehow give insight into the implosion of rotating stars.
The astronomers and astrophysicists had come to Dallas to discuss quasars; they were not at all interested in Kerr’s esoteric mathematical topic. So, as Kerr got up to speak, many slipped out of the lecture hall and into the foyer to argue with each other about their favorite theories of quasars. Others, less polite, remained seated in the hall and argued in whispers. Many of the rest catnapped in a fruitless effort to remedy their sleep deficits from late-night science. Only a handful of relativists listened, with rapt attention.
This was more than Achilles Papapetrou, one of the world’s leading relativists, could stand. As Kerr finished, Papapetrou demanded the floor, stood up, and with deep feeling explained the importance of Kerr’s feat. He, Papapetrou, had been trying for thirty years to find such a solution of Einstein’s equation, and had failed, as had many other relativists. The astronomers and astrophysicists nodded politely, and then, as the next speaker began to hold forth on a theory of quasars, they refocused their attention, and the meeting picked up pace.
T he 1960s marked a turning point in the study of radio sources. Previously the study was totally dominated by observational astron?mers—that is, optical astronomers and the radio-observing experimental physicists, who were now being integrated into the astronomical community and called radio astronomers. Theoretical astrophysicists, by contrast, had contributed little, because the radio observations were not yet detailed enough to guide their theorizing very much. Their only contributions had been the realization that the radio waves are produced by high-speed electrons spiraling around magnetic field lines in the giant radio-emitting lobes, and their calculation of how much magnetic and kinetic energy this entails.
In the 1960s, as the resolutions of radio telescopes continued to improve and optical observations began to reveal new features of the radio sources (for example, the tiny sizes of the light-emitting cores of quasars), this growing body of information became grist for the minds of astrophysicists. From this rich information, the astrophysicists generated dozens of detailed models to explain radio galaxies and quasars, and then one by one their models were disproved by accumulating observational data. This, at last, was how science was supposed to work!
One key piece of information was the radio astronomers’ discovery that radio galaxies emit radio waves not only from their giant double lobes, one on each side of the central galaxy, but also from the core of the central galaxy itself. In 1971, this suggested to Martin Rees, a recent student of Dennis Sciama’s in Cambridge, a radically new idea about the powering of the double lobes. Perhaps a single engine in the galaxy’s core was responsible for all the galaxy’s radio waves. Perhaps this engine was directly energizing the core’s radio-emitting electrons and magnetic fields, perhaps it was also beaming up power to the giant lobes, to energize their electrons and fields, and perhaps this engine in the cores of radio galaxies was of the same sort (whatever that might be) that powers quasars.
Rees initially suspected that the beams that carry power from the core to the lobes were made of ultra-Iow-frequency electromagnetic waves. However, theoretical calculations soon made it clear that such electromagnetic beams cannot penetrate through the galaxy’s interstellar gas, no matter how hard they try.
As is often the case, Rees’s not quite correct idea stimulated a correct one. Malcolm Longair, Martin Ryle, and Peter Scheuer in Cambridge took the idea and modified it in a simple way: They kept Rees’s beams, but made them of hot, magnetized gas rather than electromagnetic waves. Rees quickly agreed that this kind of gas jet would do the job, and with his student Roger Blandford he computed the properties that the gas jets should have.
A few years later, this prediction, that the radio-emitting lobes are powered by jets of gas emerging from a central engine, was spectacularly confirmed using huge new radio interferometers in Britain, Holland, and America—most notably the American VLA (very large array) on the plains of St. Augustin in New Mexico (Figure 9.5). The interferometers saw the jets, and the jets had just the predicted properties. They reached from the galaxy’s core to the two lobes, and they could even be seen ramming into gas in the lobes and being slowed to a halt.
The VLA uses the same “spots on the bowl” technique as the radio interferometers of the 1940s and 1950s (Figure 9.2), but its bowl is much larger and it uses many more spots (many more linked radio telescopes). It achieves resolutions as good as 1 arc second, about the same as the world’s best optical telescopes—a tremendous achievement when one contemplates the crudeness of Jansky’s and Reber’s original instruments forty years earlier. But the improvements did not stop there. By the early 1980s, pictures of the cores of radio galaxies and quasars, with resolutions 1000 times better than optical telescopes, were being produced by very long baseline inteiferometers (VLBIs) composed of radio telescopes on opposite sides of a continent or the world. (The output of each telescope in a VLBI is recorded on magnetic tape, along with time markings from an atomic clock, and the tapes from all the telescopes are then played into a computer where they are “interfered” with each other to make the pictures.)

9.5 The VLA radio interferometer on the plains of St. Augustin in New Mexico. [courtesy NRAO/AUI.]
A picture of the radio emission from the radio galaxy Cygnus A made with the VLA by R. A. Perley, J.W. Dreyer, and JJ. Cowan. The jet that feeds the right-hand radio lobe is quite clear; the jet feeding the left lobe is much fainter. Notice the enormous improvement in resolution of this radio-wave picture compared with Reber’s 1944 contour map which did not show the double lobes at all (Figure 9.1d), and with Jennison and Das Gupta’s 1953 radio map which barely revealed the existence of the lobes (two rectangles in Figure 9.3d), and with Ryle’s 1969 contour map (Figure 9.3d). [courtesy NRAO/AUI.]
These VLBI pictures showed, in the early 1980s, that the jets extend right into the innermost few light-years of the core of a galaxy or quasar—the very region in which resides, in the case of some quasars such as 3C273, a brilliantly luminous, light-emitting object no larger than a light-month in size. Presumably the central engine is inside the light-emitting object, and it is powering not only that object, but also the jets, which then feed the radio lobes.
The jets gave yet another clue to the nature of the central engine. Some jets were absolutely straight over distances of a million light-years or more. If the source of such jets were turning, then, like a rotating water nozzle on a sprinkler, it would produce bent jets. The observed jets’ straightness thus meant that the central engine had been firing its jets in precisely the same direction for a very long time. How long? Since the jets’ gas cannot move faster than the speed of light, and since some straight jets were longer than a million light-years, the firing direction must -have been steady for more than a million years. To achieve such steadiness, the engine’s “nozzles,” which eject the jets, must be attached to a superbly steady object—a long-lived gyroscope of some sort. (Recall that a gyroscope is a rapidly spinning object that holds the direction of its spin axis steadily fixed over a very long time. Such gyroscopes are key components of inertial navigation systems for airplanes and missiles.)
Of the dozens of ideas that had been proposed by the early 1980s to explain the central engine, only one entailed a superb gyroscope with a long life, a size less than a light-month, and an ability to generate powerful jets. That unique idea was a gigantic, spinning black hole.
Gigantic Black Holes
T he idea that gigantic black holes might power quasars and radio galaxies was conceived by Edwin Salpeter and Yakov Borisovich Zel’dovich in 1964 (the first year of the golden age—Chapter 7 ). This idea was an obvious application of the Salpeter–Zel’dovich discovery that gas streams, falling toward a black hole, should collide and radiate (see Figure 8.4).
A more complete and realistic description of the fall of gas streams toward a black hole was devised in 1969 by Donald Lynden-Bell, a British astrophysicist in Cambridge. Lynden-Bell argued, convincingly, that after the gas streams collide, they will join together, and then centrifugal forces will make them spiral around and around the hole many times before falling in; and as they spiral, they will form a disk-shaped object, much like the rings around the planet Saturn—san accretion disk Lynden-Bell called it, since the gas is “accreting” onto the hole. (The right half of Figure 8.7 shows an artist’s conception of such an accretion disk around the modest-sized hole in Cygnus X-l.) In the accretion disk, adjacent gas streams will rub against each other, and intense friction from that rubbing will heat the disk to high temperatures.
In the 1980s, astrophysicists realized that the brilliant light-emitting object at the center of 3C273, the object 1 light-month or less in size, was probably Lynden-Bell’s friction-heated accretion disk.
We normally think of friction as a poor source of heat. Recall the unfortunate Boy Scout who tries to start a fire by rubbing two sticks together! However, the Boy Scout is limited by his meager muscle power, while an accretion disk’s friction feeds off gravitational energy. Since the gravitational energy is enormous, far larger than nuclear energy, the friction is easily up to the task of heating the disk and making it shine 100 times more brightly than the most luminous galaxies.
H ow can a black hole act as a gyroscope? James Bardeen and Jacobus Petterson of Yale University realized the answer in 1975: If the black hole spins rapidly, then it behaves precisely like a gyroscope. Its spin direction remains always firmly fixed and unchanging, and the swirl of space near the hole created by the spin (Figure 7.7) remains always firmly oriented in the same direction. Bardeen and Petterson showed by a mathematical calculation that this near-hole swirl of space must grab the inner part of the accretion disk and hold it firmly in the hole’s equatorial plane—and must do so no matter how the disk is oriented far from the hole (Figure 9.6). As new gas from interstellar space is captured into the distant part of the disk, it may change the distant disk’s orientation, but it can never change the disk’s orientation near the hole. The hole’s gyroscopic action prevents it. Near the hole the disk remains always in the hole’s equatorial plane.
Without Kerr’s solution to the Einstein field equation, this gyroscopic action would have been unknown, and it might have been impossible to explain quasars. With Kerr’s solution in hand, astrophysicists in the mid-1970s were arriving at a clear and elegant explanation. For the first time, the concept of a black hole as a dynamical body, more than just a “hole in space,” was playing a central role in explaining astronomers’ observations.
How strong will the swirl of space be near the gigantic hole? In other words, how fast will gigantic holes spin? James Bardeen deduced the answer: He showed mathematically that gas accreting into the hole from its disk should gradually make the hole spin faster and faster. By the time the hole has swallowed enough inspiraling gas to double its mass, the hole should be spinning at nearly its maximum possible rate—the rate beyond which centrifugal forces prevent any further speedup (Chapter 7 ). Thus, gigantic holes should typically have near-maximal spins.

9.6 The spin of a black hole produces a swirl of space around the hole, and that swirl holds the inner part of the accretion disk in the hole’s equatorial plane.
H ow can a black hole and its disk produce two oppositely pointed jets? Amazingly easily, Blandford, Rees, and Lynden-Bell at Cambridge University recognized in the mid-1970s. There are four possible ways to produce jets; anyone of them might do the job.
First, Blandford and Rees realized, the disk may be surrounded by a cool gas cloud (Figure 9.7a). A wind blowing off the upper and lower faces of the disk (analogous to the wind that blows off the Sun’s surface) may create a bubble of hot gas inside the cool cloud. The hot gas may then punch orifices in the cool cloud’s upper and lower faces and flow out of them. Just as a nozzle on a garden hose collimates outflowing water to form a fast, thin stream, so the orifices in the cool cloud should collimate the outflowing hot gas to form thin jets. The directions of the jets will depend on the locations of the orifices. The most likely locations, if the cool cloud spins about the same axis as the black hole, are along the common spin axis, that is, perpendicular to the plane of the inner part of the accretion disk—and the orifices at these locations will produce jets whose direction is anchored to the black hole’s gyroscopic spin.
Second, because the disk is so hot, its internal pressure is very high, and this pressure might puff the disk up until it becomes very thick (Figure 9.7b). In this case, Lynden-Bell pointed out, the orbital motion of the disk’s gas will produce centrifugal forces that create whirlpool-like funnels in the top and bottom faces of the disk. These funnels are precisely analogous to the vortex that sometimes forms when water swirls down the drainhole of a bathtub. The black hole is like the drainhole, and the disk’s gas is like the water. The faces of the vortex-like funnels should be so hot, because of friction in the gas, that they blow a strong wind off themselves, and the funnels might then collimate this wind into jets, Lynden-Bell reasoned. The jets’ directions will be the same as the funnels’, which in turn are firmly anchored to the hole’s gyroscopic spin axis.
Third, Blandford realized, magnetic field lines anchored in the disk and sticking out of it will be forced, by the disk’s orbital motion, to spin around and around (Figure 9.7c). The spinning field lines will assume an outward and upward (or outward and downward) spiraling shape. Electrical forces should anchor hot gas (plasma) onto the spinning field lines; the plasma can slide along the field lines but not across them. As the field lines spin, centrifugal forces should fling the plasma outward along them to form two magnetized jets, one shooting outward and upward, the other outward and downward. Again the jets’ directions will be firmly anchored to the hole’s spin.
9.7 Four methods by which a black hole or its accretion disk could power twin jets. (a) A wind from the disk blows a bubble in a surrounding, spinning gas cloud; the bubble’s hot gas punches orifices through the cloud, along its spin axis; and jets of hot gas shoot out the orifices. (b) The disk is puffed up by the pressure of its great internal heat, and the surface of the puffed, rotating disk forms two funnels that collimate the disk’s wind into two jets. (c) Magnetic field lines anchored in the disk are forced to spin by the disk’s orbital rotation; as they spin, the field lines fling plasma upward and downward, and the plasma, sliding along the field lines, forms two magnetized jets. (d) Magnetic field lines threading through the black hole are forced to spin by the swirl of the hole’s space, and as they spin, the field lines fling plasma upward and downward to form two magnetized jets.
The fourth method of producing jets is more interesting than the others and requires more explanation. In this fourth method, the hole is threaded by magnetic field lines as shown in Figure 9.7d. As the hole spins, it drags the field lines around and around, causing them to fling plasma upward and downward in much the same manner as the third method, to form two jets. The jets shoot out along the hole’s spin axis and their direction thus is firmly anchored to the hole’s gyroscopic spin. This method was conceived of by Blandford soon after he received his Ph.D. in Cambridge, together with a Cambridge graduate student, Roman Znajek, and it thus is called the Blandford–Znajek process.
The Blandford–Znajek process is especially interesting, because the power that goes into the jets comes from the hole’s enormous rotational energy. (This should be obvious since it is the hole’s spin that causes space to swirl, and the swirl of space that causes the magnetic field lines to rotate, and the field lines’ rotation that flings plasma outward.)
How is it possible, in this Blandford–Znajek process, for the hole’s horizon to be threaded by magnetic field lines? Such field lines would be a form of “hair” that can be converted into electromagnetic radiation and be radiated away, and therefore, according to Price’s theorem (Chapter 7 ), they must be radiated away. In fact, Price’s theorem is correct only if the black hole is sitting alone, far from all other objects. The hole we are discussing, however, is not alone; it is surrounded by an accretion disk. If the field lines of Figure 9.7d pop off the hole, the lines going out the hole’s northern hemisphere and those going out its southern hemisphere will turn out to be continuations of each other, and the only way these lines can then escape is by pushing their way out through the accretion disk’s hot gas. But the hot gas will not let the field lines through; it confines them firmly into the region of space inside the disk’s inner face, and since most of that region is occupied by the hole, most of the confined field lines thread through the hole.
Where do these magnetic field lines come from? From the disk itself. All gas in the Universe is magnetized, at least a little bit, and the disk’s gas is no exception. 4 As, bit by bit, the disk’s gas accretes into the hole, it carries its magnetic field lines with it. Upon nearing the hole, each bit of gas slides down its magnetic field lines and through the horizon, leaving the field lines behind, sticking out of the horizon and threading it in the manner of Figure 9.7d. These threading field lines, firmly confined by the surrounding disk, should then extract the hole’s rotational energy by the Blandford–Znajek process.
All four methods of producing jets (orifices in a gas cloud, wind from a funnel, whirling field lines anchored in a disk, and the Blandford–Znajek process) probably operate, to varying degrees, in quasars, in radio galaxies, and in the peculiar cores of some other types of galaxies (cores that are called active galactic nuclei).
I f quasars and radio galaxies are powered by the same kind of black-hole engine, what makes them look so different? Why does the light of a quasar appear to come from an intensely luminous, star-like object, 1 light-month in size or less, while the light of a radio galaxy comes from a Milky Way–like assemblage of stars, 100,000 light-years in size?
It seems almost certain that quasars are not much different from radio galaxies; their central engines are also surrounded by a 100,000-light-year-sized galaxy of stars. However, in a quasar, the central black hole is fueled at an especially high rate by accreting gas (Figure 9.8), and frictional heating in the disk is correspondingly high. This huge heating makes the disk shine so strongly that its optical brilliance is hundreds or thousands of times greater than that of all the stars in the surrounding galaxy put together. Astronomers, blinded by the brilliance of the disk, cannot see the galaxy’s stars, and thus the object looks “quasi-stellar” (that is, star-like; like a tiny, intense point of light) instead of looking like a galaxy. 5
The innermost region of the disk is so hot that it emits X-rays; a little farther out, the disk is cooler and emits ultraviolet radiation; still farther out it is cooler still and emits optical radiation (light); and in its outermost region it is even cooler and emits infrared radiation. The light-emitting region is typically about a light-year in size, though in some cases such as 3C273 it can be a light-month or smaller and thus can vary in brightness over periods as short as a month. Much of the X-ray radiation and ultraviolet light pouring out of the innermost region hits and heats gas clouds several light-years from the disk; it is those heated clouds that emit the spectral lines by which the quasars were first discovered. A magnetized wind blowing off the disk, in some quasars but not all, will be strong enough and well enough collimated to produce radio-emitting jets.
9.8 Our best present understanding of the structures of quasars and radio galaxies. This detailed model, based on all the observational data, has been developed by Sterl Phinney of Caltech and others.
In a radio galaxy, by contrast with a quasar, the central accretion disk presumably is rather quiescent. Quiescence means small friction in the disk, and thus small heating and low luminosity, so that the disk shines much less brightly than the rest of the galaxy. Astronomers thus see the galaxy and not the disk through their optical telescopes. However, the disk, the spinning hole, and magnetic fields threading through the hole together produce strong jets, probably in the manner of Figure 9.7d (the Blandford–Znajek process), and those jets shoot out through the galaxy and into intergalactic space, where they feed energy into the galaxy’s huge radio-emitting lobes.
T hese black-hole-based explanations for quasars and radio galaxies are so successful that it is tempting to assert they must be right, and a galaxy’s jets must be a unique signature crying out to us “I come from a black hole!” However, astrophysicists are a bit cautious. They would like a more ironclad case. It is still possible to explain all the observed properties of radio galaxies and quasars using an alternative, non–black-hole engine: a rapidly spinning, magnetized, supermassive star, one weighing millions or billions of times as much as the Sun—a type of star that has never been seen by astronomers, but that theory suggests might form at the centers of galaxies. Such a supermassive star would behave much like a hole’s accretion disk. By contracting to a small size (but a size still larger than its critical circumference), it could release a huge amount of gravitational energy; that energy, by way of friction, could heat the star so it shines brightly like an accretion disk; and magnetic field lines anchored in the star could spin and fling out plasma in jets.
It might be that some radio galaxies or quasars are powered by such supermassive stars. However, the laws of physics insist that such a star should gradually contract to a smaller and smaller size, and then, as it nears its critical circumference, should implode to form a black hole. The star’s total lifetime before implosion should be much less than the age of the Universe. This suggests that, although the youngest of radio galaxies and quasars might be powered by supermassive stars, older ones are almost certainly powered, instead, by gigantic holes —almost certainly, but not absolutely certainly. These arguments are not ironclad.
H ow common are gigantic black holes? Evidence, gradually accumulated during the 1980s, suggests that such holes inhabit not only the cores of most quasars and radio galaxies, but also the cores of most large, normal (non-radio) galaxies such as the Milky Way and Andromeda, and even the cores of some small galaxies such as Andromeda’s dwarf companion, M32. In normal galaxies (the Milky Way, Andromeda, M32) the black hole presumably is surrounded by no accretion disk at all, or by only a tenuous disk that pours out only modest amounts of energy.
The evidence for such a hole in our own Milky Way galaxy (as of 1993) is suggestive, but far from firm. One key bit of evidence comes from the orbital motions of gas clouds near the center of the galaxy. Infrared observations of those clouds, by Charles Townes and colleagues at the University of California at Berkeley, show that they are orbiting around an object which weighs about 3 million times as much as the Sun, and radio observations reveal a very peculiar, though not strong, radio source at the position of the central object—a radio source amazingly small, no larger than our solar system. These are the types of observations one might expect from a quiescent, 3-million-solar-mass black hole with only a tenuous accretion disk; but they are also readily explained in other ways.
T he possibility that gigantic black holes might exist and inhabit the cores of galaxies came as a tremendous surprise to astronomers. In retrospect, however, it is easy to understand how such holes might form in a galactic core.
In any galaxy, whenever two stars pass near each other, their gravitational forces swing them around each other and then fling them off in directions different from their original paths. (This same kind of swing and fling changes the orbits of NASA’s spacecraft when they encounter planets such as Jupiter.) In the swing and fling, one of the stars typically gets flung inward, toward the galaxy’s center, while the other gets flung outward, away from the center. The cumulative effect of many such swings and flings is to drive some of the galaxy’s stars deep down into the galaxy’s core. Similarly, it turns out, the cumulative effect of friction in the galaxy’s interstellar gas is to drive much of the gas down into the galaxy’s core.
As more and more gas and stars accumulate in the core, the gravity of the agglomerate they form should become stronger and stronger. Ultimately, the agglomerate’s gravity may become so strong as to overwhelm its internal pressure, and the agglomerate may implode to form a gigantic hole. Alternatively, massive stars in the agglomerate may implode to form small holes, and those small holes may collide with each other and with stars and gas to form ever larger and larger holes, until a single gigantic hole dominates the core. Estimates of the time required for such implosions, collisions, and coalescences make it seem plausible (though not compelling) that most galaxies will have grown gigantic black holes in their cores long before now.
If astronomical observations did not strongly suggest that the cores of galaxies are inhabited by gigantic black holes, astrophysicists even today, in the 1990s, would probably not predict it. However, since the observations do suggest gigantic holes, astrophysicists easily accommodate themselves to the suggestion. This is indicative of our poor understanding of what really goes on in the cores of galaxies.
W hat of the future? Need we worry that the gigantic hole in our Milky Way galaxy might swallow the Earth? A few numbers set one’s mind at ease. Our galaxy’s central hole (if it indeed exists) weighs about 3 million times what the Sun weighs, and thus has a circumference of about 50 million kilometers, or 200 light-seconds—about onetenth the circumference of the Earth’s orbit around the Sun. This is tiny by comparison with the size of the galaxy itself. Our Earth, along with the Sun, is orbiting around the galaxy’s center on an orbit with a circumference of 200,000 light-years—about 30 billion times larger than the circumference of the hole. If the hole were ultimately to swallow most of the mass of the galaxy, its circumference would expand only to about 1 light-year, still 200,000 times smaller than the circumference of our orbit.
Of course, in the roughly 10 18 years (100 million times the Universe’s present age) that it will require for our central hole to swallow a large fraction of the mass of our galaxy, the orbit of the Earth and Sun will change substantially. It is not possible to predict the details of those changes, since we do not know well enough the locations and motions of all the other stars that the Sun and Earth may encounter during 10 18 years. Thus, we cannot predict whether the Earth and Sun will wind up, ultimately, inside the galaxy’s central hole, or will be flung out of the galaxy. However, we can be confident that, if the Earth ultimately gets swallowed, its demise is roughly 10 18 years in the future—so far off that many other catastrophes will almost certainly befall the Earth and humanity in the meantime.
1. By light, I always mean in this book the type of electromagnetic waves that the human eye can see; that is, optical radiation.
2. See Figure 7.3. Ginzburg is best known not for these discoveries, but for yet another: his development, with Lev Landau, of the “Ginzburg–Landau theory” of superconductivity (that is, an explanation for how it is that some metals, when made very cold, lose all their resistance to the flow of electricity). Ginzburg is one of the world’s few true “Renaissance physicists,” a man who has contributed significantly to almost all branches of theoretical physics.
3. For background, see the entry “antimatter” in the glossary, and Footnote 2 in Chapter 5 .
4. The magnetic fields have been built up continually over the life of the Universe by the motions of interstellar and stellar gas, and once generated, the magnetic fields are extremely hard to get rid of. When interstellar gas accumulates into the accretion disk, it carries its magnetic fields with itself.
5. The word “quasar” is shorthand for “quasi-stellar.”