in which Hermann Minkowski
unifies space and time,
and Einstein warps them
Minkowski’s Absolute Spacetime
The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth, space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.
W ith these words Hermann Minkowski revealed to the world, in September 1908, a new discovery about the nature of space and time.
Einstein had shown that space and time are “relative.” The length of an object and the flow of time are different when viewed from different reference frames. My time differs from yours if I move relative to you, and my space differs from yours. My time is a mixture of your time and your space; my space is a mixture of your space and your time.
Minkowski, building on Einstein’s work, had now discovered that the Universe is made of a four-dimensional “spacetime” fabric that is absolute, not relative. This four-dimensional fabric is the same. as seen from all reference frames (if only one can learn how to “see” it); it exists independently of reference frames.
The following tale (adapted from Taylor and Wheeler, 1992) illustrates the idea underlying Minkowski’s discovery.
O nce upon a time, on an island called Mledina in a far-off Eastern sea, there lived a people with strange customs and taboos. Each June, on the longest day of the year, all the Mledina men journeyed in a huge sailing vessel to a distant, sacred island called Serona, there to commune with an enormous toad. All night long the toad would enchant them with marvelous tales of stars and galaxies, pulsars and quasars. The next day the men would sail back to Mledina, filled with inspiration that sustained them for the whole of the following year.
Each December, on the longest night of the year, the Mledina women sailed to Serona, communed with the same toad all the next day, and returned the next night, inspired with the toad’s visions of stars and galaxies, quasars and pulsars.
Now, it was absolutely taboo for any Mledina woman to describe to any Mledina man her journey to the sacred island of Serona, or any details of the toad’s tales. The Mledina men were ruled by the same taboo. Never must they expose to a woman anything about their annual voyage.
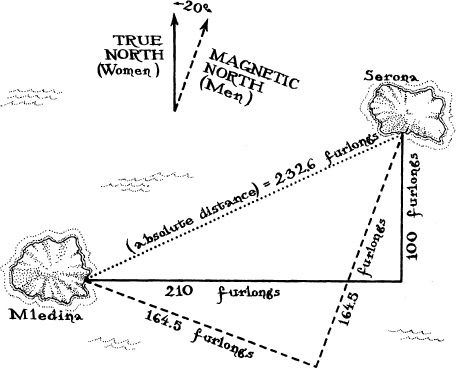
In the summer of 1905 a radical Mledina youth named Albert, who cared little for the taboos of his culture, discovered and exposed to all the Mledinans, female and male, two sacred maps. One was the map by which the Mledina priestess guided the sailing vessel on the women’s midwinter journey. The other was the map used by the Mledina priest on the men’s midsummer voyage. What shame the men felt, having their sacred map exposed. The women’s shame was no less. But there the maps were, for everyone to see—and they contained a great shock: They disagreed about the location of Serona. The women were sailing eastward 210 furlongs, then northward 100 furlongs, while the men were sailing eastward 164.5 furlongs, then northward 164.5 furlongs. How could this be? Religious tradition was firm; the women and the men were to seek their annual inspiration from the same sacred toad on the same sacred island of Serona.
Most of the Mledinans dealt with their shame by pretending the exposed maps were fakes. But a wise old Mledina man named Hermann believed. For three years he struggled to understand the mystery of the maps’ discrepancy. Finally, one autumn day in 1908, the truth came to him: The Mledina men must be navigating by magnetic compass, and the Mledina women by the stars (Figure 2.1). The Mledina men reckoned north and east magnetically, the Mledina women reckoned them by the rotation of the Earth which makes the stars turn overhead, and the two methods of reckoning differed by 20 degrees. When the men sailed northward, as reckoned by them, they were actually sailing “north 20 degrees east,” or about 80 percent north and 20 percent east, as reckoned by the women. In this sense, the men’s north was a mixture of the women’s north and east, and similarly the women’s north was a mixture of the men’s north and west.
The key that led Hermann to this discovery was the formula of Pythagoras: Take two legs of a right triangle; square the length of one leg, square the length of the other, add them, and take the square root. The result should be the length of the triangle’s hypotenuse.
The hypotenuse was the straight-line path from Mledina to Serona. The absolute distance along that straight-line path was 
= 232.6 furlongs as reckoned using the women’s map with its legs along true east and true north. As reckoned using the men’s map with its legs along magnetic east and magnetic north, the absolute distance was 
. furlongs. The eastward distance and the northward distance were “relative”; they depended on whether the map’s reference frame was magnetic or true. But from either pair of relative distances one could compute the same, absolute, straight-line distance.
2.1 The two maps of the route from Mledina to Serona superimposed on each other, together with Hermann’s notations of magnetic north, true north, and the absolute distance.
History does not record how the people of Mledina, with their culture of taboos, responded to this marvelous discovery.
H ermann Minkowski’s discovery was analogous to the discovery by Hermann the Mledinan: Suppose that you move relative to me (for example, in your ultra-high-speed sports car). Then:
• Just as magnetic north is a mixture of true north and true east, so also my time is a mixture of your time and your space.
• Just as magnetic east is a mixture of true east and true south, so also my space is a mixture of your space and your time.
• Just as magnetic north and east, and true north and east, are merely different ways of making measurements on a preexisting, two-dimensional surface—the surface of the Earth—so also my space and time, and your space and time, are merely different ways of making measurements on a preexisting, four-dimensional “surface” or “fabric,” which Minkowski called spacetime.
• Just as there is an absolute, straight-line distance on the surface of the Earth from Mledina to Serona, computable from Pythagoras’s formula using either distances along magnetic north and east or distances along true north and east, so also between any two events in spacetime there is an absolute straight-line interval computable from an analogue of Pythagoras’s formula using lengths and times measured in either reference frame, mine or yours.
It was this analogue of Pythagoras’s formula (I shall call it Minkowski’s formula) that led Hermann Minkowski to his discovery of absolute spacetime.
The details of Minkowski’s formula will not be important in the rest of this book. There is no need to master them (though for readers who are curious, they are spelled out in Box 2.1). The only important thing is that events in spacetime are analogous to points in space, and there is an absolute interval between any two events in spacetime completely analogous to the straight-line distance between any two points on a flat sheet of paper. The absoluteness of this interval (the fact that its value is the same, regardless of whose reference frame is used to compute it) demonstrates that spacetime has an absolute reality; it is a four-dimensional fabric with properties that are independent of one’s motion.
Box 2.1
Minkowski’s Formula
You zoom past me in a powerful, 1-kilometer-long sports car, at a speed of 162,000 kilometers per second (54 percent of the speed of light); recall Figure 1.3. Your car’s motion is shown in the following spacetime diagrams. Diagram (a) is drawn from your viewpoint; (b) from mine. As you pass me, your car backfires, ejecting a puff of smoke from its tailpipe; this backfire event is labeled B in the diagrams. Two microseconds (two-millionths of a second) later, as seen by you, a firecracker on your front bumper detonates; this detonation event is labeled D.
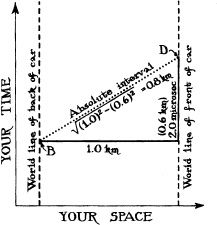
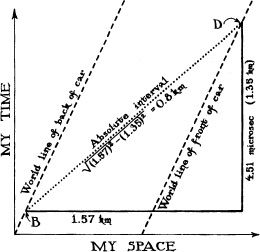
Because space and time are relative (your space is a mixture of my space and my time), you and I disagree about the time separation between the backfire event B and the detonation event D. They are separated by 2.0 microseconds of your time, and by 4.51 microseconds of mine. Similarly, we disagree about the events’ spatial separation; it is 1.0 kilometer in your space and 1.57 kilometers in mine. Despite these temporal and spatial disagreements, we agree that the two events are separated by a straight line in four-dimensional spacetime, and we agree that the “absolute interval” along that line (the spacetime length of the line) is 0.8 kilometer. (This is analogous to the Mledinan men and women agreeing on the straight-line distance between Mledina and Serona.)
We can use Minkowski’s formula to compute the absolute interval: We each multiply the events’ time separation by the speed of light (299,792 kilometers per second), getting the rounded-off numbers shown in the diagrams (0.600 kilometer for you, 1.35 kilometers for me). We then square the events’ time and space separations, we subtract the squared time separation from the squared space separation, and we take the square root. (This is analogous to the Mledinans squaring the eastward and northward separations, adding them, and taking the square root.) As is shown in the diagrams, although your time and space separations differ from mine, we get the same final answer for the absolute interval: 0.8 kilometer.
There is only one important difference between Minkowski’s formula, which you and I follow, and Pythagoras’s formula, which the Mledinans follow: Our squared separations are to be subtracted rather than added. This subtraction is intimately connected to the physical difference between spacetime, which you and I are exploring, and the Earth’s surface, which the Mledinans explore—but at the risk of infuriating you, I shall forgo explaining the connection, and simply refer you to the discussions in Taylor and Wheeler (1992).
As we shall see in the coming pages, gravity is produced by a curvature (a warpage) of spacetime’s absolute, four-dimensional fabric, and black holes, wormholes, gravitational waves, and singularities are all constructed wholly and solely from that fabric; that is, each of them is a specific type of spacetime warpage.
Because the absolute fabric of spacetime is responsible for such fascinating phenomena, it is frustrating that you and I do not experience it in our everyday lives. The fault lies in our low-velocity technology (for example, sports cars that travel far more slowly than light). Because of our low velocities relative to each other, we experience space and time solely as separate entities, we never notice the discrepancies between the lengths and times that you and I measure (we never notice that space and time are relative), and we never notice that our relative spaces and times are unified to form spacetime’s absolute, four-dimensional fabric.
M inkowski, you may recall, was the mathematics professor who had labeled Einstein a lazy dog in his student days. In 1902 Minkowski, a Russian by birth, had left the ETH in Zurich to take up a more attractive professorship in Göttingen, Germany. (Science was as international then as it is now.) In Göttingen, Minkowski studied Einstein’s article on special relativity, and was impressed. That study led him to his 1908 discovery of the absolute nature of four-dimensional spacetime.
When Einstein learned of Minkowski’s discovery, he was not impressed. Minkowski was merely rewriting the laws of special relativity in a new, more mathematical language; and, to Einstein, the mathematics obscured the physical ideas that underlie the laws. As Minkowski continued to extol the beauties of his spacetime viewpoint, Einstein began to make jokes about Göttingen mathematicians describing relativity in such complicated language that physicists wouldn’t be able to understand it.
The joke, in fact, was on Einstein. Four years later, in 1912, he would realize that Minkowski’s absolute spacetime is an essential foundation for incorporating gravity into special relativity. Sadly, Minkowski did not live to see this; he died of appendicitis in 1909, at age forty-five.
I shall return to Minkowski’s absolute spacetime later in this chapter. First, however, I must develop another thread of my story: Newton’s law of gravity and Einstein’s first steps toward reconciling it with special relativity, steps he took before he began to appreciate Minkowski’s breakthrough.
Newton’s Gravitational Law, and Einstein’s First Steps to Marry It to Relativity
N ewton conceived of gravity as a force that acts between every pair of objects in the Universe, a force that pulls the objects toward each other. The larger the objects’ masses and the closer they are together, the stronger the force. Stated more precisely, the force is proportional to the product of the objects’ masses and inversely proportional to the square of the distance between them.
This gravitational law was an enormous intellectual triumph. When combined with Newton’s laws of motion, it explained the orbits of the planets around the Sun, and the moons around the planets, the ebb and flow of ocean tides, and the fall of rocks; and it taught Newton and his seventeenth-century compatriots how to weigh the Sun and the Earth. 1
During the two centuries that separated Newton and Einstein, astronomers’ measurements of celestial orbits improved manyfold, putting Newton’s gravitational law to ever more stringent tests. Occasionally new astronomical measurements disagreed with Newton’s law, but in due course the observations or their interpretation turned out to be wrong. Time after time Newton’s law triumphed over experimental or intellectual error. For example, when the motion of the planet Uranus (which had been discovered in 1781) appeared to violate the predictions of Newton’s gravitational law, it seemed likely that the gravity of some other, undiscovered planet must be pulling on Uranus, perturbing its orbit. Calculations by U. J. J. Le Verrier, based solely on Newton’s laws of gravity and motion and on the observations of Uranus, predicted where in the sky that new planet should be. In 1846, when J. G. Galle trained his telescope on the spot, there the predicted planet was, too dim to be seen by the naked eye but bright enough for his telescope. This new planet, which vindicated Newton’s gravitational law, was given the name “Neptune.”
In the early 1900s, there remained two other exquisitely small, but puzzling discrepancies with Newton’s gravitational law. One, a peculiarity in the orbit of the planet Mercury, would ultimately turn out to herald a failure of Newton’s law. The other, a peculiarity in the Moon’s orbit, would ultimately go away; it would turn out to be a misinterpretation of the astronomers’ measurements. As is so often the case with exquisitely precise measurements, it was difficult to discern which of the two discrepancies, if either, should be worried about.
Einstein correctly suspected that Mercury’s peculiarity (an anomalous shift of its perihelion; Box 2.2) was real and the Moon’s peculiarity was not. Mercury’s peculiarity “smelled” real; the Moon’s did not. However, this suspected disagreement of experiment with Newton’s gravitational law was far less interesting and important to Einstein than his conviction that Newton’s law would turn out to violate his newly formulated principle of relativity (the “metaprinciple” that all the laws of physics must be the same in every inertial reference frame). Since Einstein believed firmly in his principle of relativity, such a violation would mean that Newton’s gravitational law must be flawed. 2
Box 2.2
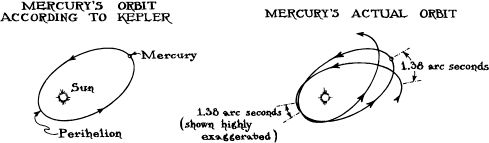
The Perihelion Shift of Mercury
Kepler described the orbit of Mercury as an ellipse with the Sun at one focus (left diagram, in which the elliptical elongation of the orbit is exaggerated). However, by the late 1800s astronomers had deduced from their observations that Mercury’s orbit is not quite elliptical. After each trip around its orbit, Mercury fails by a tiny amount to return to the same point as it started. This failure can be described as a shift, with each orbit, in the location of Mercury’s closest point to the Sun (a shift of its perihelion). Astronomers measured a perihelion shift of 1.38 seconds of arc during each orbit (right diagram, in which the shift is exaggerated).
Newton’s law of gravity could account for 1.28 arc seconds of this 1.38-arc-second shift: It was produced by the gravitational pull of Jupiter and the other planets on Mercury. However, there remained a 0.10-arc-second discrepancy: an anomalous 0.10-arc-second shift of Mercury’s perihelion during each orbit The astronomers claimed that the errors and uncertainties in their measurement were only 0.01 arc second in size, but considering the tiny angles being measured (0.01 arc second is equivalent to the angle subtended by a human hair at a distance of 2 kilometers), it is not surprising that many physicists of the late nineteenth and early twentieth centuries were skeptical, and expected Newton’s laws to triumph in the end.
Einstein’s reasoning was simple: According to Newton, the gravitational force depends on the distance between the two gravitating objects (for example, the Sun and Mercury), but according to relativity, that distance is different in different reference frames. For example, Einstein’s relativity laws predict that the distance between the Sun and Mercury will differ by about a part in a billion, depending on whether one is riding on Mercury’s surface when measuring it or riding on the surface of the Sun. If both reference frames, Mercury’s and the Sun’s, are equally good in the eyes of the laws of physics, then which frame should be used to measure the distance that appears in Newton’s gravitational law? Either choice, Mercury’s frame or the Sun’s, would violate the principle of relativity. This quandary convinced Einstein that Newton’s gravitational law must be flawed.
Einstein’s audacity is breathtaking. Having discarded Newton’s absolute space and absolute time with almost no experimental justification, he was now inclined to discard Newton’s enormously successful law of gravity, and with even less experimental justification. However, he was motivated not by experiment, but by his deep, intuitive insight into how the laws of physics ought to behave.
E instein began his search for a new law of gravity in 1907. His initial steps were triggered and guided by a writing project: Although the patent office now classified him as only a “technical expert second class” (recently promoted from third class), he was sufficiently respected by the world’s great physicists to be invited to write a review article for the annual publication Jahrbuch der Radioaktivität und Elektronik about his special relativistic laws of physics and their consequences. As he worked on his review, Einstein discovered a valuable strategy for scientific research: The necessity to lay out a subject in a self-contained, coherent, pedagogical manner forces one to think about it in new ways. One is driven to examine all the subject’s gaps and flaws, and seek cures for them.
Gravity was his subject’s biggest gap; special relativity, with its inertial frames on which no gravitational force can act, was totally ignorant of gravity. So while Einstein wrote, he kept looking for ways to incorporate gravity into his relativistic laws. As happens to most people immersed in a puzzle, even when Einstein wasn’t thinking directly about this problem, the back of his mind mulled it over. Thus it was that one day in November 1907, in Einstein’s own words, “I was sitting in a chair in the patent office at Bern, when all of a sudden a thought occurred to me: ‘If a person falls freely, he will not feel his own weight.’”
Now you or I could have had that thought, and it would not have led anywhere. But Einstein was different. He pursued ideas to their ultimate ends; he wrung from them every morsel of insight that he could. And this idea was key; it pointed toward a revolutionary new view of gravity. He later called it “the happiest thought of my life.”
The consequences of this thought tumbled forth quickly, and were immortalized in Einstein’s review article. If you fall freely (for example, by jumping off a cliff), not only will you not feel your own weight, it will seem to you, in all respects, as though gravity had completely disappeared from your vicinity. For example, if you drop some rocks from your hand as you fall, you and the rocks will then fall together, side by side. If you look at the rocks and ignore your other surroundings, you cannot discern whether you and the rocks are falling together toward the ground below or are floating freely in space, far from all gravitating bodies. In fact, Einstein realized, in your immediate vicinity, gravity is so irrelevant, so impossible to detect, that all the laws of physics, in a small reference frame (laboratory) that you carry with you as you fall, must be the same as if you were moving freely through a universe without gravity. In other words, your small, freely falling reference frame is “equivalent to” an inertial reference frame in a gravity-free universe, and the laws of physics that you experience are the same as those in a gravity-free inertial frame; they are the laws of special relativity. (We shall learn later why the reference frame must be kept small, and that “small” means very small compared to the size of the Earth—or, more generally, very small compared to the distance over which the strength and direction of gravity change.)
As an example of the equivalence between a gravity-free inertial frame and your small, freely falling frame, consider the special relativistic law that describes the motion of a freely moving object (let it be a cannonball) in a universe without gravity. As measured in any inertial frame in that idealized universe, the ball must move along a straight line and with uniform velocity. Compare this with the ball’s motion in our real, gravity-endowed Universe: If the ball is fired from a cannon on a grassy meadow on Earth and is watched by a dog who sits on the grass, the ball arcs up and over and falls back to Earth (Figure 2.2). It moves along a parabola (solid black curve) as measured in the dog’s reference frame. Einstein asks that you view this same cannonball from a small, freely falling reference frame. This is easiest if the meadow is at the edge of a cliff. Then you can jump off the cliff just as the cannon is fired, and watch the ball as you fall.
As an aid in depicting what you see as you fall, imagine that you hold in front of yourself a window with twelve panes of glass, and you watch the ball through your window (middle segment of Figure 2.2). As you fall, you see the clockwise sequence of scenes shown in Figure 2.2. In looking at this sequence, ignore the dog, cannon, tree, and cliff; focus solely on your windowpanes and the ball. As seen by you, relative to your windowpanes, the ball moves along the straight dashed line with constant velocity.
Thus, in the dog’s reference frame the ball obeys Newton’s laws; it moves along a parabola. In your small, freely falling reference frame it obeys the laws of gravity-free special relativity; it moves along a straight line with constant velocity. And what is true in this example must be true in general, Einstein realized in a great leap of insight:
In any small freely falling reference frame anywhere in our rea4 gravity-endowed Universe, the laws of physics must be the same as they are in an inertial reference frame in an idealized, gravity-free universe. Einstein called this the principle of equivalence, because it asserts that small, freely falling frames in the presence of gravity are equivalent to inertial frames in the absence of gravity.
This assertion, Einstein realized, had an enormously important consequence: It implied that, if we merely give the name “inertial reference frame” to every small, freely falling reference frame in our real, gravity-endowed Universe (for example, to a little laboratory that you carry as you fall over the cliff), then everything that special relativity says about inertial frames in an idealized universe without gravity will automatically also be true in our real Universe. Most important, the principle of relativity must be true: All small, inertial (freely falling) reference frames in our real, gravity-endowed Universe must be “created equal”; none can be preferred over any other in the eyes of the laws of physics. Or, stated more precisely (see Chapter 1 ):
Formulate any law of physics in terms of measurements made in one smal4 inertial (freely falling) reference frame. Then, when restated in terms of measurements in any other small inertial (freely falling) frame, that law of physics must take on precisely the same mathematical and logical form as in the original frame. And this must be true whether the (freely falling) inertial frame is in gravity-free intergalactic space, or is falling off a cliff on Earth, or is at the center of our galaxy, or is falling through the horizon of a black hole.
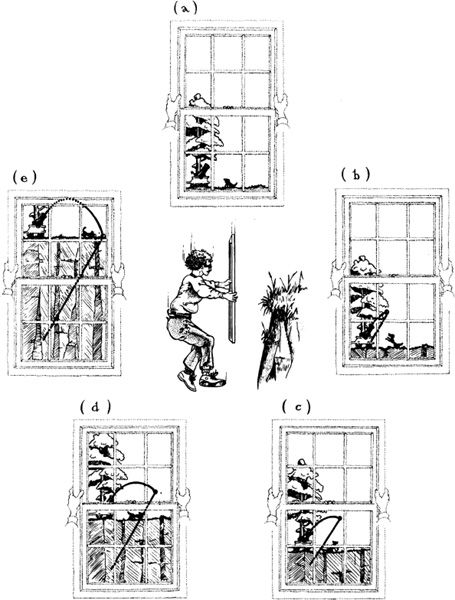
2.2 Center: You jump off a cliff holding a twelve-paned window in front of yourself. Remainder of figure, clockwise from the top: What you see through the window when a cannon is fired. Relative to the falling window frame, the ball’s trajectory is the straight, dashed line; relative to the dog and the Earth’s surface, it is the solid parabola.
With this extension of his principle of relativity to include gravity, Einstein took his first step toward a new set of gravitational laws—his first step from special relativity to general relativity.
B e patient, dear reader. This chapter is probably the most difficult one in the book. My story will get less technical in the next chapter, when we start exploring black holes.
W ithin days after formulating his equivalence principle, Einstein used it to make an amazing prediction, called gravitational time dilation: If one is at rest relative to a gravitating body, then the nearer one is to the body, the more slowly one’s time must flow. For example, in a room on Earth, time must flow more slowly near the floor than near the ceiling. This Earthly difference turns out to be so minuscule, however (only 3 parts in 10 16 ; that is, 300 parts in a billion billion), that it is exceedingly difficult to detect. By contrast (as we shall see in the next chapter), near a black hole gravitational time dilation is enormous: If the hole weighs 10 times as much as the Sun, then time will flow 6 million times more slowly at 1 centimeter height above the hole’s horizon than far from its horizon; and right at the horizon, the flow of time will be completely stopped. (Imagine the possibilities for time travel: If you descend to just above a black hole’s horizon, hover there for one year of near-horizon time flow, and then return to Earth, you will find that during that one year of your time, millions of years have flown past on Earth!)
Einstein discovered gravitational time dilation by a somewhat complicated argument, but later he produced a simple and elegant demonstration of it, one that illustrates beautifully his methods of physical reasoning. That demonstration is presented in Box 2.4, and the Doppler shift of light, on which it relies, is explained in Box 2.3.
W hen starting to write his 1907 review article, Einstein expected it to describe relativity in a universe without gravity. However, while writing, he had discovered three clues to the mystery of how gravity might mesh with his relativity laws—the equivalence principle, gravitational time dilation, and the extension of his principle of relativity to include gravity—so he incorporated those clues into his article. Then, around the beginning of December, he mailed the article off to the editor of the Jahrbuch der Radioaktivität und Elektronik and turned his attention full force to the challenge of devising a complete, relativistic description of gravity.
Box 2.3
Doppler Shift
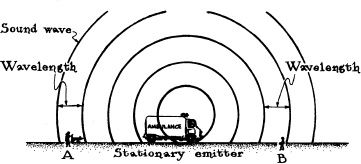
Whenever an emitter and a receiver of waves are moving toward each other, the receiver sees the waves shifted to higher frequency—that is, shorter period and shorter wavelength. If the emitter and receiver are moving apart, then the receiver sees the waves shifted to lower frequency—that is, longer period and longer wavelength. This is called the Doppler shift, and it is a property of all types of waves: sound waves, waves on water, electromagnetic waves, and so forth.
For sound waves, the Doppler shift is a familiar everyday phenomenon. One hears it in the sudden lowering of the sound’s pitch when a speeding ambulance passes with siren screeching (drawing b), or when a landing airplane passes overhead. One can understand the Doppler shift by thinking about the diagrams below.
What is true of waves is also true of pulses. If the emitter transmits regularly spaced pulses of light (or of anything else), then the receiver, as the emitter moves toward it, will encounter the pulses at a higher frequency (a shorter time between pulses) than the frequency with which they were emitted.
Box 2.4
Gravitational Time Dilation
Take two identical clocks. Place one on the floor of a room beside a hole into which it later will fall, and attach the other to the room’s ceiling by a string. The ticking of the floor clock is regulated by the flow of time near the floor, and the ticking of the ceiling clock is regulated by the flow of time near the ceiling.
Let the ceiling clock emit a very short pulse of light whenever it ticks, and direct the pulses downward, toward the floor clock. Immediately before the ceiling clock emits its first pulse, cut the string that holds it, so it is falling freely. If the time between ticks is very short, then at the moment it next ticks and emits its second pulse, the clock will have fallen only imperceptibly and will still be very nearly at rest with respect to the ceiling (diagram a). This in turn means that the clock is still feeling the same flow of time as does the ceiling itself; that is, the interval between its pulse emissions is governed by the ceiling’s time flow.
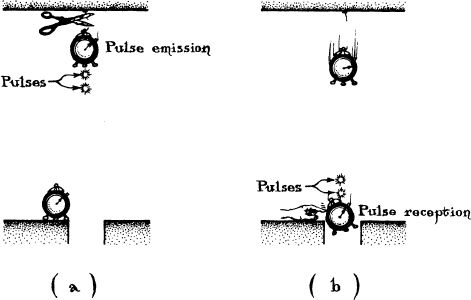
Immediately before the first pulse of light reaches the floor, drop the floor clock into the hole (diagram b). The second pulse arrives so soon afterward that the freely falling floor clock has moved imperceptibly between pulses, and is still very nearly at rest with respect to the floor, and therefore is still feeling the same flow of time as does the floor itself.
In this way, Einstein converted the problem of comparing the flow of time as felt by the ceiling and the floor into the problem of comparing the ticking rates of two freely falling clocks: the falling ceiling clock which feels ceiling time, and the falling floor clock which feels floor time. Einstein’s equivalence principle then permitted him to compare the ticks of the freely falling clocks with the aid of his special relativistic laws.
Because the ceiling clock was dropped before the floor clock, its downward speed is always greater than that of the floor clock (diagram b); that is, it moves toward the floor clock. This implies that the floor clock will see the ceiling clock’s light pulses Doppler-shifted (Box 2.3); that is, it will see them arrive more closely spaced in time than the time between its own ticks. Since the time between pulses was regulated by the ceiling’s time flow, and the time between floor-clock ticks is regulated by the floor’s time flow, this means that time must flow more slowly near the floor than near the ceiling; in other words, gravity must dilate the flow of time.
On December 24, he wrote to a friend saying, “At this time I am busy with considerations on relativity theory in connection with the law of gravitation ... I hope to clear up the so-far unexplained secular changes of the perihelion shift of Mercury . . . but thus far it does not seem to work.” By early 1908, frustrated by no real progress, Einstein gave up, and turned his attention to the realm of atoms, molecules, and radiation (the “realm of the small”), where the unsolved problems for the moment seemed more tractable and interesting. 3
Through 1908 (while Minkowski unified space and time, and Einstein pooh-poohed the unification), and through 1909, 1910, and 1911, Einstein stayed with the realm of the small. These years also saw him move from the patent office in Bern to an associate professorship at the University of Zurich, and a full professorship in Prague—a center of the Austro-Hungarian empire’s cultural life.
Einstein’s life as a professor was not easy. He found it irritating to have to give regular lectures on topics not close to his research. He could summon neither the energy to prepare such lectures well nor the enthusiasm to make them scintillate, even though when lecturing on topics dear to his heart, he was brilliant. Einstein was now a full-fledged member of Europe’s academic circle, but he was paying a price. Despite this price, his research in the realm of the small moved forward impressively, producing insights that later would win him the Nobel Prize (see Box 4.1).
Then, in mid-1911, Einstein’s fascination with the small waned and his attention returned to gravity, with which he would struggle almost full time until his triumphant formulation of general relativity in November 1915.
The initial focus of Einstein’s gravitational struggle was tidal gravitational forces.
Tidal Gravity and Spacetime Curvature
I magine yourself an astronaut out in space, far above the Earth’s equator, and falling freely toward it. Although, as you fall, you will not feel your own weight, you will, in fact, feel some tiny, residual effects of gravity. Those residuals are called “tidal gravity,” and they can be understood by thinking about the gravitational forces you feel, first from the viewpoint of someone watching you from the Earth below, and then from your own viewpoint.
2.3 As you fall toward Earth, tidal gravitational forces stretch you from head to foot and squeeze you from the sides.
As seen from Earth (Figure 2.3a), the gravitational pull is slightly different on various parts of your body. Because your feet are closer to the Earth than your head, gravity pulls more strongly on them than on your head, so it stretches you from foot to head. And because gravity pulls always toward the Earth’s center, a direction that is slightly leftward on your right side and slightly rightward on your left side, the pull is slightly leftward on your right and slightly rightward on your left; that is, it squeezes your sides inward.
From your viewpoint (Figure 2.3b), the large, downward force of gravity is gone, vanished. You feel weightless. However, the vanished piece of gravity is only the piece that pulled you downward. The head-to-foot stretch and side-to-side squeeze remain. They are caused by the differences between gravity on the outer parts of your body and gravity at your body’s center, differences that you cannot get rid of by falling freely.
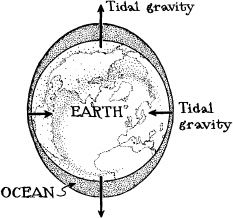
The vertical stretch and lateral squeeze that you feel, as you fall, are called tidal gravity or tidal gravitational forces, because, when the Moon is their source rather than the Earth and when the Earth is feeling them rather than you, they produce the ocean tides. See Box 2.5.
In deducing his principle of equivalence, Einstein ignored tidal gravitational forces; he pretended they do not exist. (Recall the essence of his argument: As you fall freely, you “will not feel your own weight” and “it will seem to you, in all respects, as though gravity has disappeared from your vicinity.”) Einstein justified ignoring tidal forces by imagining that you (and your reference frame) are very small. For example, if you are the size of an ant or smaller, then your body parts will all be very close to each other, the direction and strength of gravity’s pull will therefore be very nearly the same on the outer parts of your body as at its center, and the difference in gravity between your outer parts and your center, which causes the tidal stretch and squeeze, will be extremely small. On the other hand, if you are a 5000-kilometer-tall giant, then the direction and strength of the Earth’s gravitational pull will differ greatly between the outer parts of your body and its center; and correspondingly, as you fall, you will experience a huge tidal stretch and squeeze.
This reasoning convinced Einstein that, in a sufficiently small, freely falling reference frame (a frame very small compared to the distance over which gravity’s pull changes), one should not be able to detect any influences of tidal gravity whatsoever; that is, small, freely falling reference frames in our gravity-endowed Universe are equivalent to inertial frames in a universe without gravity. But not so for large frames. And the tidal forces felt in large frames seemed to Einstein, in 1911, to be a key to the ultimate nature of gravity.
Box 2.5
Ocean Tides Produced by Tidal Forces
On the side of the Earth nearest the Moon, the lunar gravity is stronger than at the Earth’s center, so it pulls the oceans toward the Moon more strongly than it pulls the solid Earth, and the oceans in response stretch outward a bit toward the Moon. On the side farthest from the Moon, the lunar gravity is weaker, so it pulls the oceans toward the Moon less strongly than it pulls the solid Earth, and the oceans in response stretch out away from the Moon. On the left side of the Earth, the Moon’s gravitational pull, which points toward the Moon’s center, has a slight rightward component, and on the right side it has a slight leftward component; and these components squeeze the oceans inward. This pattern of oceanic stretch and squeeze produces two high tides and two low tides each day, as the Earth rotates
If the tides at your favorite ocean beach do not behave in precisely this way, it is not the fault of the Moon’s gravity; rather, it is because of two effects: (1) There is a lag in the water’s response to the tidal gravity. It takes time for the water to move in and out of bays, harbors, river channels, fjords, and other indentations in the coastline. (2) The Sun’s gravitational stretch and squeeze are about half as strong on the Earth as the Moon’s, but are oriented differently because the Sun’s position in the sky is (usually) different from the Moon’s. The Earth’s tides are a result of the combined tidal gravity of the Sun and the Moon.
I t was clear how Newton’s gravitational law explains tidal forces: They are produced by a difference in the strength and direction of gravity’s pull, from one place to another. But Newton’s law, with its gravitational force that depends on distance, had to be wrong; it violated the principle of relativity (“in whose frame was the distance to be measured?”). Einstein’s challenge was to formulate a completely new gravitational law that is simultaneously compatible with the principle of relativity and explains tidal gravity in some new, simple, compelling way.
From mid-1911 to mid-1912, Einstein tried to explain tidal gravity by assuming that time is warped, but space is flat. This radical-sounding idea was a natural outgrowth of gravitational time dilation: The different rates of flow of time near the ceiling and the floor of a room on Earth could be thought of as a warpage of time. Perhaps, Einstein speculated, a more complicated pattern of time warpage might produce all known gravitational effects, from tidal gravity to the elliptical orbits of the planets to even the anomalous perihelion shift of Mercury.
After a twelve-month pursuit of this intriguing idea, Einstein abandoned it, and for a good reason. Time is relative. Your time is a mixture of my time and my space (if we move with respect to each other), and therefore, if your time is warped but your space is flat, then my time and my space must both be warped, as must be everybody else’s. You and only you will have a flat space, so the laws of physics must be picking out your reference frame as fundamentally different from all others—in violation of the principle of relativity.
Nevertheless, time warpage “smelled right” to Einstein, so perhaps—he reasoned—everybody’s time is warped and, inevitably alongside that, everybody’s space is warped. Perhaps these combined warpages could explain tidal gravity.
The idea of a warpage of both time and space was rather daunting. Since the Universe admits an infinite number of different reference frames, each moving with a different velocity, there would have to be an infinity of warped times and an infinity of warped spaces! Fortunately, Einstein realized, Hermann Minkowski had provided a powerful tool for simplifying such complexity: “Henceforth, space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.” There is just one, unique, absolute, four-dimensional spacetime in our Universe; and a warpage of everyone’s time and everyone’s space must show up as a warpage of Minkowski’s single, unique, absolute spacetime.
This was the conclusion to which Einstein was driven in the summer of 1912 (though he preferred to use the word “curvature” rather than “warpage”). After four years of ridiculing Minkowski’s idea of absolute spacetime, Einstein had finally been driven to embrace it, and warp it.
W hat does it mean for spacetime to be curved (or warped)? For clarity, ask first what it means for a two-dimensional surface to be curved (or warped). Figure 2.4 shows a flat surface and a curved surface. On the flat surface (an ordinary sheet of paper) are drawn two absolutely straight lines. The lines start out side by side and parallel. The ancient Greek mathematician Euclid, who created the subject now called “Euclidean geometry,” used as one of his geometric postulates the demand that two such initially parallel lines never cross. This non-crossing is an unequivocal test for the flatness of the surface on which the lines are drawn. If space is flat, then initially parallel straight lines can never cross. If we ever find a pair of initially parallel straight lines that do cross, then we will know that space is not flat.
The curved surface in Figure 2.4 is a globe of the Earth. Locate on that globe the city of Quito, Equador; it sits on the equator. Send out a precisely straight line from Quito, directed northward. The line will travel northward, at constant longitude, through the North Pole.
In what sense is this a straight line? In two senses. One is the sense so crucial to airlines: It is a great circle, and the great circles on the Earth’s globe are the shortest routes between two points and thus are the kinds of routes along which airlines like to fly. Construct any other line connecting Quito to the North Pole; it will necessarily be longer than the great circle.
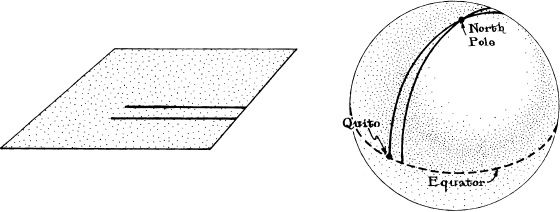
2.4 Two straight lines, initially parallel, never cross on a flat surface such as the sheet of paper shown on the left. Two straight lines, initially parallel, will typically cross on a curved surface such as the globe of the world shown on the right.
The second sense of straightness is the one that we shall use below, when discussing spacetime: In sufficiently small regions on the globe along the great circle’s route, the globe’s curvature can hardly be noticed. In such a region, the great circle looks straight in the usual flat-sheet-of-paper sense of straightness—the sense of straightness used by professional surveyors, who lay out boundaries of property using transits or laser beams. The great circle is straight, in this surveyors’ sense, in each and every small region along its route.
Mathematicians use the name geodesic for any line, on a curved or warped surface, that is straight in these two senses: the airlines’ “shortest route” sense, and the surveyors’ sense.
Now move eastward on the globe from Quito by a few centimeters, and construct a new straight line (great circle; geodesic) that is precisely parallel, at the equator, to the one through Quito. This straight line, like the first one, will pass through the globe’s North Pole. It is the curvature of the globe’s surface that forces the two straight lines, initially parallel to cross at the North Pole.
W ith this understanding of the effects of curvature in two-dimensional surfaces, we can return to four-dimensional spacetime and ask about curvature there.
In an idealized universe without gravity, there is no warpage of space, no warpage of time; spacetime has no curvature. In such a universe, according to Einstein’s special relativity laws, freely moving particles must travel along absolutely straight lines. They must maintain constant direction and constant velocity, as measured in any and every inertial reference frame. This is a fundamental tenet of special relativity.
Now, Einstein’s equivalence principle guarantees that gravity cannot change this fundamental tenet of free motion: Whenever a freely moving particle, in our real, gravity-endowed Universe, enters and passes through a small, inertial (freely falling) reference frame, the particle must move along a straight line through that frame. Straight-line motion through a small inertial frame, however, is the obvious analogue of straight-line behavior as measured by surveyors in a small region of the Earth’s surface; and just as such straight-line behavior in small regions on Earth implies that a line is actually a geodesic of the Earth’s surface, so also the particle’s straight-line motion in small regions of spacetime implies that the particle moves along a geodesic of spacetime. And what is true of this particle must be true of all particles: Every freely moving particle (every particle on which no forces, except gravity, act) travels along a geodesic of spacetime.
As soon as Einstein realized this, it became obvious to him that tidal gravity is a manifestation of spacetime curvature.
To understand why, imagine the following thought experiment (mine, not Einstein’s). Stand on the ice sheet at the North Pole, holding two small balls, one in each hand (Figure 2.5). Throw the balls into the air side by side, so they rise upward along precisely parallel trajectories,and then watch them fall back to Earth. Now, in a thought experiment such as this, you can do anything you wish so long as it does not violate the laws of physics. You wish to watch the trajectories of the balls as they fall under the action of gravity, not only above the Earth’s surface, but also below. For this purpose, you can pretend that the balls are made of a material that falls through the Earth’s soil and rock without being slowed at all (tiny black holes would have this property), and you can pretend that you and a friend on the opposite side of the Earth, who also watches, can follow the balls’ motion inside the Earth via “X-ray vision.”
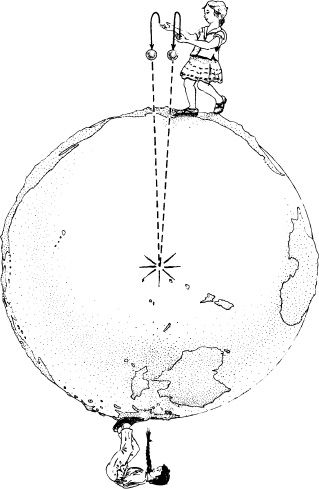
2.5 Two balls thrown into the air on precisely parallel trajectories, if able to pass unimpeded through the Earth, will collide near the Earth’s center.
As the balls fall into the Earth, the Earth’s tidal gravity squeezes them together in the same way as it squeezes your sides if you are a falling astronaut (Figure 2.3). The strength of the tidal gravity is just right to make both balls fall almost precisely toward the Earth’s center, and hit each other there.
Now comes the payoff of this thought experiment: Each ball moved along a precisely straight line (a geodesic) through spacetime. Initially the two straight lines were parallel. Later they crossed (the balls collided). This crossing of initially parallel, straight lines signals a curvature of spacetime. From Einstein’s viewpoint, spacetime curvature causes the crossing, that is, causes the balls’ collision, just as the curvature of the globe caused straight lines to cross in Figure 2.4. From Newton’s viewpoint, tidal gravity causes the crossing.
Thus, Einstein and Newton, with their very different viewpoints on the nature of space and time, give very different names to the agent that causes the crossing. Einstein calls it spacetime curvature; Newton calls it tidal gravity. But there is just one agent acting. Therefore, spacetime curvature and tidal gravity must be precisely the same thing, expressed in different languages.
Our human minds have great difficulty visualizing curved surfaces with more than two dimensions; therefore, it is nearly impossible to visualize the curvature of four-dimensional spacetime. Some insight can be gained, however, by looking at various two-dimensional pieces of spacetime. Figure 2.6 uses two such pieces to explain how spacetime curvature creates the tidal stretch and squeeze that produce the ocean tides.
Figure 2.6a depicts one piece of spacetime in the vicinity of Earth, a piece that includes time, plus space along the direction toward the Moon. The Moon curves this piece of spacetime, and the curvature stretches apart two geodesics, in the manner shown. Correspondingly,we humans see two freely moving particles, which travel along the geodesics, get stretched apart as they travel, and we interpret that stretching as a tidal gravitational force. This stretching tidal force (spacetime curvature) affects not only freely moving particles, but also the Earth’s oceans; it stretches the oceans in the manner shown in Box 2.5, producing oceanic bulges on the sides of the Earth nearest and farthest from the Moon. The two bulges are trying to travel along geodesics of the curved spacetime (Figure 2.6a), and therefore are trying to fly apart; but the Earth’s gravity (the spacetime curvature produced by the Earth; not shown in the diagram) is counteracting that flight, so the ocean merely bulges.
Figure 2.6b is a different piece of spacetime near Earth, a piece that includes time, plus space along a direction transverse to the Moon’s direction. The Moon curves this piece of spacetime, and the curvature squeezes geodesics together in the manner shown. Correspondingly, we humans see freely moving particles that travel along geodesics transverse to the Moon’s direction get squeezed together by the curvature (by the Moon’s tidal gravity), and similarly we see the Earth’s oceans get squeezed along directions transverse to the direction of the Moon. This tidal squeeze produces the transverse oceanic compressions shown in Box 2.5.
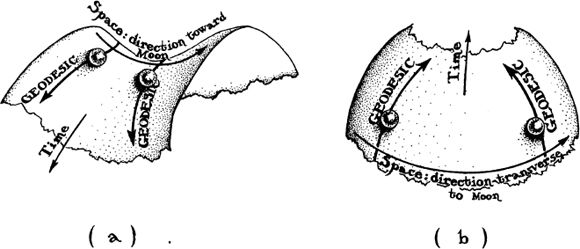
2.6 Two two-dimensional pieces of curved spacetime, in the vicinity of the Earth. The curvature is produced by the Moon. The curvature creates a tidal stretch along the direction toward the Moon (a), and a tidal squeeze along the direction transverse to the Moon (b), and this stretch and squeeze produce the ocean’s tides in the manner discussed in Box 2.5, above.
E instein was a professor in Prague in the summer of 1912, when he realized that tidal gravity and spacetime curvature are one and the same thing. It was a wonderful revelation—though he was not yet certain of it and did not yet understand it as fully as I have described it, and it did not provide a complete explanation of gravity. It told Einstein that spacetime curvature dictates the motion of free particles and raises the tides on the ocean, but it did not tell him how the curvature is produced. Einstein believed that the matter inside the Sun and Earth and other planets is somehow responsible for the curvature. But how? How does matter warp spacetime, and what are the details of the warpage? A quest for the law of warpage became Einstein’s central concern.
A few weeks after “discovering” spacetime curvature, Einstein moved from Prague back to Zurich, to take up a professorship at his alma mater, the ETH. Upon arriving in Zurich in August 1912, Einstein sought advice from an old classmate, Marcel Grossmann, who was now a professor of mathematics there. Einstein explained his idea that tidal gravity is spacetime curvature, and then asked whether any mathematician had ever developed a set of mathematical equations that could help him figure out the law of warpage, that is, the law that describes how matter forces spacetime to curve. Grossmann, whose specialty was other aspects of geometry, wasn’t sure, but after browsing in the library he came back with an answer: Yes, the necessary equations did exist. They had been invented largely by the German mathematician Bernhard Riemann in the 1860s, the Italian Gregorio Ricci in the 1880s, and Ricci’s student Tullio Levi-Civita in the 1890s and 1900s; they were called the “absolute differential calculus” (or, in physicists’ language of 1915–1960, “tensor analysis,” or in the language of 1960 to the present, “differential geometry”). But, Grossmann told Einstein, this differential geometry is a terrible mess which physicists should not be involved with. Were there any other geometries that could be used to figure out the law of warpage? No.
And so, with much help from Grossmann, Einstein set out to master the intricacies of differential geometry. As Grossmann taught mathematics to Einstein, Einstein taught something of physics to Grossmann. Einstein later quoted Grossmann as saying, “I concede that I did after all gain something rather important from the study of physics. Before, when I sat on a chair and felt a trace of heat left by my ‘pre-sitter,’ I used to shudder a little. That is completely gone, for on this point physics has taught me that heat is something completely impersonal.”
Learning differential geometry was not an easy task for Einstein. The spirit of the subject was alien to the intuitive physical arguments that he found so natural. In late October 1912 he wrote to Arnold Sommerfeld, a leading German physicist: “I am now occupying myself exclusively with the problem of gravitation and believe that, with the aid of a local mathematician [Grossmann] who is a friend of mine I’ll now be able to master all the difficulties. But one thing is certain, that in all my life I have never struggled so hard, and that I have been infused with great respect for mathematics the subtler parts of which, in my simple-mindedness, I had considered pure luxury up to now! Compared to this problem the original relativity theory [special relativity] is child’s play.”
Together Einstein and Grossmann struggled through the autumn and into the winter with the puzzle of how matter forces spacetime to curve. But despite their all-out effort, the mathematics could not be brought into accord with Einstein’s vision. The law of warpage eluded them.
Einstein was convinced that the law of warpage should obey a generalized (enlarged) version of his principle of relativity: It should look the same in every reference frame—not just inertial (freely falling) frames, but non-inertial frames as well. The law of warpage should not rely for its formulation on any special reference frame or any special class of reference frames whatsoever. 4 Sadly, the equations of differential geometry did not seem to admit such a law. Finally, in late winter, Einstein and Grossmann gave up the search and published the best law of warpage they could find—a law that relied for its definition on a special class of reference frames.
Einstein, eternally the optimist, managed to convince himself, briefly, that this was no catastrophe. To his physicist friend Paul Ehrenfest he wrote in early 1913, “What can be more beautiful than that this necessary specialization follows from [the mathematical equations for the conservation of energy and momentum]?” But after further thought he regarded it a disaster. He wrote to Lorentz in August 1913: “My faith in the reliability of the theory [the “law of warpage”] still fluctuates. . . . [Because of the failure to obey the generalized principle of relativity,] the theory contradicts its own starting point and all is up in the air.”
As Einstein and Grossmann struggled with spacetime curvature, other physicists scattered over the European continent took up the challenge of uniting the laws of gravity with special relativity. But none of them—Gunnar Nordstrom in Helsinki, Finland; Gustav Mie in Greifswald, Germany; Max Abraham in Milano, Italy—adopted Einstein’s spacetime curvature viewpoint. Instead they treated gravity, like electromagnetism, as due to a force field which lives in Minkowski’s flat, special relativistic spacetime. And no wonder they took this approach: The mathematics used by Einstein and Grossmann was horrendously complex, and it had produced a law of warpage that violated its authors’ own precepts.
Controversy swirled among the proponents of the various viewpoints. Wrote Abraham, “Someone who, like this author, has had to warn repeatedly against the siren song of [the principle of relativity] will greet with satisfaction the fact that its originator has now convinced himself of its untenability.” Wrote Einstein in reply, “In my opinion the situation does not indicate the failure of the relativity principle. . . . There is not the slightest ground to doubt its validity.” And privately he described Abraham’s theory of gravity as “a stately horse which lacks three legs.” Writing to friends in 1913 and 1914 Einstein said of the controversy, “I enjoy it that this affair is at least taken up with the requisite animation. I enjoy the controversies. Figaro mood: I’ll play him a tune.” “I enjoy it that colleagues occupy themselves at all with the theory [developed by Grossmann and me], although for the time being with the purpose of killing it. ... On the face of it, Nordstrom’s theory ... is much more plausible. But it, too, is built on [flat, Minkowskian spacetime], the belief in which amounts, I feel, to something like a superstition.”
I n April 1914 Einstein left the ETH for a professorship in Berlin which carried no teaching duties. At last he could work on research as much as he wished, and even do so in the stimulating vicinity of Berlin’s great physicists, Max Planck and Walther Nernst. In Berlin, despite the June 1914 outbreak of the First World War, Einstein continued his quest for an acceptable description of how matter curves space-time, a description that did not rely on any special class of reference frames—an improved law of warpage.
A three-hour train ride from Berlin, in the university village of Gottingen where Minkowski had worked, there lived one of the greatest mathematicians of all time: David Hilbert. During 1914 and 1915 Hilbert pursued a passionate interest in physics. Einstein’s published ideas fascinated him, so in late June of 1915 he invited Einstein down for a visit. Einstein stayed for about a week and gave six two-hour lectures to Hilbert and his colleagues. Several days after the visit Einstein wrote to a friend, “I had the great joy of seeing in Göttingen that everything [about my work] is understood to the last detail. With Hilbert I am just enraptured.”
Several months after returning to Berlin, Einstein became more deeply distressed than ever with the Einstein-Grossmann law of warpage. Not only did it violate his vision that the laws of gravity should be the same in all reference frames, but also, he discovered after arduous calculation, it gave a wrong value for the anomalous perihelion shift of Mercury’s orbit. He had hoped his theory would explain the perihelion shift, thereby triumphantly resolving the shift’s discrepancy with Newton’s laws. Such an achievement would give at least some experimental confirmation that his laws of gravity were right and Newton’s wrong. However, his calculation, based on the Einstein—Grossmann law of warpage, gave a perihelion shift half as large as was observed.
Pouring over his old calculations with Grossmann, Einstein discovered a few crucial mistakes. Feverishly he worked through the month of October, and on 4 November he presented, at the weekly plenary session of the Prussian Academy of Sciences in Berlin, an account of his mistakes and a revised law of warpage—still slightly dependent on a special class of reference frames, but less so than before.
Remaining dissatisfied, Einstein struggled all the next week with his 4 November law, found mistakes, and presented yet another proposal for the law of warpage at the Academy meeting of 11 November. But still the law relied on special frames; still it violated his principle of relativity.
Resigning himself to this violation, Einstein struggled during the next week to compute consequences of his new law that could be observed with telescopes. It predicted, he found, that starlight passing the limb of the Sun should be deflected gravitationally by an angle of 1.7 seconds of arc (a prediction that would be verified four years later by careful measurements during a solar eclipse). More important to Einstein, the new law yielded the correct perihelion shift for Mercury! He was beside himself with joy; for three days he was so excited that he couldn’t work. This triumph he presented at the next meeting of the Academy on 18 November.
But his law’s violation of the relativity principle still troubled him. So during the next week Einstein poured back over his calculations and found another mistake—the crucial one. At last everything fell into place. The entire mathematical formalism was now free of any dependence on special reference frames: It had the same form when expressed in each and every reference frame (see Box 2.6 below) and thus obeyed the principle of relativity. Einstein’s vision of 1914 was fully vindicated! And the new formalism still gave the same predictions for the shift of Mercury’s perihelion and for the gravitational deflection of light, and it incorporated his 1907 prediction of gravitational time dilation. These conclusions, and the final definitive form of his general relativity law of warpage, Einstein presented to the Prussian Academy on 25 November.
Three days later Einstein wrote to his friend Arnold Sommerfeld: “During the past month I had one of the most exciting and strenuous times of my life, but also one of the most successful.” Then, in a January letter to Paul Ehrenfest: “Imagine my joy [that my new law of warpage obeys the principle of relativity] and at the result that the [law predicts] the correct perihelion motion of Mercury. I was beside myself with ecstasy for days.” And, later, speaking of the same period: “The years of searching in the dark for a truth that one feels but cannot express, the intense desire and the alternations of confidence and misgiving until one breaks through to clarity and understanding, are known only to him who has himself experienced them.”
R emarkably, Einstein was not the first to discover the correct form of the law of warpage, the form that obeys his relativity principle. Recognition for the first discovery must go to Hilbert. In autumn 1915, even as Einstein was struggling toward the right law, making mathematical mistake after mistake, Hilbert was mulling over the things he had learned from Einstein’s summer visit to Göttingen. While he was on an autumn vacation on the island of Rugen in the Baltic the key idea came to him, and within a few weeks he had the right law—derived not by the arduous trial-and-error path of Einstein, but by an elegant, succinct mathematical route. Hilbert presented his derivation and the resulting law at a meeting of the Royal Academy of Sciences in Göttingen on 20 November 1915, just five days before Einstein’s presentation of the same law at the Prussian Academy meeting in Berlin.
Quite naturally, and in accord with Hilbert’s own view of things, the resulting law of warpage was quickly given the name the Einstein field equation (Box 2.6) rather than being named after Hilbert. Hilbert had carried out the last few mathematical steps to its discovery independently and almost simultaneously with Einstein, but Einstein was responsible for essentially everything that preceded those steps: the recognition that tidal gravity must be the same thing as a warpage of spacetime, the vision that the law of warpage must obey the relativity principle, and the first 90 percent of that law, the Einstein field equation. In fact, without Einstein the general relativistic laws of gravity might not have been discovered until several decades later.
Box 2.6
The Einstein Field Equation: Einstein’s Law of Spacetime Warpage
Einstein’s law of spacetime warpage, the Einstein field equation, states that “mass and pressure warp spacetime.” More specifically:
At any location in spacetime, choose an arbitrary reference frame. In that reference frame, explore the curvature of spacetime by studying how the curvature (that is, tidal gravity) pushes freely moving particles together or pulls them apart along each of the three directions of the chosen frame’s space: the east–west direction, the north–south direction, and the up–down direction. The particles move along geodesics of spacetime (Figure 2.6), and the rate at which they are pushed together or pulled apart is proportional to the strength of the curvature along the direction between them. If they are pushed together as in diagrams (a) and (b), the curvature is said to be positive; if they are pulled apart as in (c), the curvature is negative.
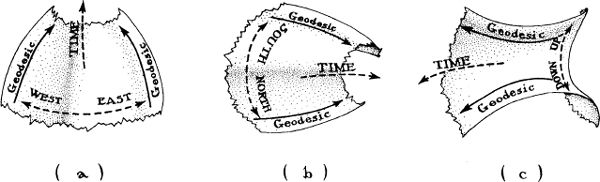
Add together the strengths of the curvatures along all three directions, east–west [diagram (a)], north–south [diagram (b)], and up–down [diagram (c)]. Einstein’s field equation states that the sum of the strengths of these three curvatures is proportional to the density of mass in the particle’s vicinity (multiplied by the speed of light squared to convert it into a density of energy; see Box 5.2), plus 3 times the pressure of matter in the particles’ vicinity.
Even though you and I may be at the same location in spacetime (say, flying over Paris, France, at noon on 14 July 1996), if we move relative to each other, your space will be different from mine and similarly the density of mass (for example, the mass of the air around us) that you measure will be different from the density that I measure, and the pressure of matter (for example, the air pressure) that we measure will differ. Similarly, it turns out, the sum of the three curvatures of spacetime that you measure will be different from the sum that I measure. However, you and I must each find that the sum of the curvatures we measure is proportional to the density of mass we measure plus 3 times the pressure we measure. In this sense, the Einstein field equation is the same in every reference frame; it obeys Einstein’s principle of relativity.
Under most circumstances (for example, throughout the solar system), the pressure of matter is tiny compared to its mass density times the speed of light squared, and therefore the pressure is an unimportant contributor to spacetime curvature; the spacetime warpage is due almost solely to mass. Only deep inside neutron stars (Chapter 5 ), and in a few other exotic places, is pressure a significant contributor to the warpage.
By mathematically manipulating the Einstein field equation, Einstein and other physicists have not only explained the deflection of starlight by the Sun and the motions of the planets in their orbits, including the mysterious perihelion shift of Mercury, they have also predicted the existence of black holes (Chapter 3 ), gravitational waves (Chapter 10 ), singularities of spacetime (Chapter 13 ), and perhaps the existence of worm-holes and time machines (Chapter 14 ). The remainder of this book is devoted to this legacy of Einstein’s genius.
A s I browse through Einstein’s published scientific papers (a browsing which, unfortunately, I must do in the 1965 Russian edition of his collected works because I read no German and most of his papers have not as of 1993 been translated into English!), I am struck by the profound change of character of Einstein’s work in 1912. Before 1912 his papers are fantastic for their elegance, their deep intuition, and their modest use of mathematics. Many of the arguments are the same as those which I and my friends use in the 1990s when we teach courses on relativity. Nobody has learned to improve on those arguments. By contrast, after 1912, complex mathematics abounds in Einstein’s papers—though usually in combination with insights about physical laws. This combination of mathematics and physical insight, which only Einstein among all physicists working on gravity had in the period 1912–1915, ultimately led Einstein to the full form of his gravitational laws.
But Einstein wielded his mathematical tools with some clumsiness. As Hilbert was later to say, “Every boy in the streets of Göttingen understands more about four-dimensional geometry than Einstein. Yet, in spite of that, Einstein did the work [formulated the general relativistic laws of gravity] and not the mathematicians.” He did the work because mathematics was not enough; Einstein’s unique physical insight was also needed.
Actually, Hilbert exaggerated. Einstein was a rather good mathematician, though in mathematical technique he was not the towering figure that he was in physical insight. As a result, few of Einstein’s post-1912 arguments are presented today in the way Einstein presented them. People have learned improvements. And, with the quest to understand the laws of physics becoming more and more mathematical as the years after 1915 passed, Einstein became less and less the dominant figure he had been. The torch was passed to others.
1. See the note to page 61 for details.
2. It was not completely obvious that Newton’s gravitational law violated Einstein’s principle of relativity, because Einstein, in formulating his principle, had relied on the concept of an inertial reference frame, and this concept could not be used in the presence of gravity. (There is no way to shield a reference frame from gravity and thereby permit it to move solely under the influence of its own inertia.) However, Einstein was convinced that there must be some way to extend the sway of his relativity principle into the realm of gravity (some way to “generalize” it to include gravitational effects), and he was convinced that Newton’s gravitational law would violate that yet-to-be-formulated “generalized principle of relativity.”
3. Chapter 4 and especially Box 4.1
4. Einstein used the new phrase “general covariance” for this property, although it was just a natural extension of his principle of relativity
Black Holes Discovered and Rejected
in which Einstein’s laws
of warped spacetime
predict black holes,
and Einstein rejects the prediction
“T he essential result of this investigation,” Albert Einstein wrote in a technical paper in 1939, “is a clear understanding as to why the ‘Schwarzschild singularities’ do not exist in physical reality.” With these words, Einstein made clear and unequivocal his rejection of his own intellectual legacy: the black holes that his general relativistic laws of gravity seemed to be predicting.
Only a few features of black holes had as yet been deduced from Einstein’s laws, and the name “black holes” had not yet been coined; they were being called “Schwarzschild singularities.” However, it was clear that anything that falls into a black hole can never get back out and cannot send light or anything else out, and this was enough to convince Einstein and most other physicists of his day that black holes are outrageously bizarre objects which surely should not exist in the real Universe. Somehow, the laws of physics must protect the Universe from such beasts.
What was known about black holes, when Einstein so strongly rejected them? How firm was general relativity’s prediction that they do exist? How could Einstein reject that prediction and still maintain confidence in his general relativistic laws? The answers to these questions have their roots in the eighteenth century.
T hroughout the 1700s, scientists (then called natural philosophers) believed that gravity was governed by Newton’s laws, and that light was made of corpuscles (particles) that are emitted by their sources at a very high, universal speed. That speed was known to be about 300,000 kilometers per second, thanks to telescopic measurements of light coming from Jupiter’s moons as they orbit around their parent planet.
In 1783 John Michell, a British natural philosopher, dared to combine the corpuscular description of light with Newton’s gravitation laws and thereby predict what very compact stars should look like. He did this by a thought experiment which I repeat here in modified form:
Launch a particle from the surface of a star with some initial speed, and let it move freely upward. If the initial speed is too low, the star’s gravity will slow the particle to a halt and then pull it back to the star’s surface. If the initial speed is high enough, gravity will slow the particle but not stop it; the particle will manage to escape. The dividing line, the minimum initial speed for escape, is called the “escape velocity.” For a particle ejected from the Earth’s surface, the escape velocity is 11 kilometers per second; for a particle ejected from the Sun’s surface, it is 617 kilometers per second? or 0.2 percent of the speed of light.
Michell could compute the escape velocity using Newton’s laws of gravity, and could show that it is proportional to the square root of the star’s mass divided by its circumference. Thus, for a star of fixed mass, the smaller the circumference, the larger the escape velocity. The reason is simple: The smaller the circumference, the closer the star’s surface is to its center, and thus the stronger is gravity at its surface, and the harder the particle has to work to escape the star’s gravitational pull.
There is a critical circumference, Michell reasoned, for which the escape velocity is the speed of light. If corpuscles of light are affected by gravity in the same manner as other kinds of particles, then light can barely escape from a star that has this critical circumference. For a star a bit smaller, light cannot escape at all. When a corpuscle of light is launched from such a star with the standard light velocity of 299,792 kilometers per second, it will fly upward at first, then slow to a halt and fall back to the star’s surface; see Figure 3.1.
Michell could easily compute the critical circumference; it was 18.5 kilometers, if the star had the same mass as the Sun, and proportionately larger if the mass were larger.
3.1 The behavior of light emitted from a star that is smaller than the critical circumference, as computed in 1783 by John Michell using Newton’s laws of gravity and corpuscular description of light.
Nothing in the eighteenth-century laws of physics prevented so compact a star from existing. Thus, Michell was led to speculate that the Universe might contain a huge number of such dark stars, each living happily inside its own critical circumference, and each invisible from Earth because the corpuscles of light emitted from its surface are inexorably pulled back down. Such dark stars were the eighteenth-century versions of black holes.
Michell, who was Rector of Thornhill in Yorkshire, England, reported his prediction that dark stars might exist to the Royal Society of London on 27 November 1783. His report made a bit of a splash among British natural philosophers. Thirteen years later, the French natural philosopher Pierre Simon Laplace popularized the same prediction in the first edition of his famous work Le Systeme du Monde, without reference to Michell’s earlier work. Laplace kept his dark-star prediction in the second (1799) edition, but by the time of the third (1808) edition, Thomas Young’s discovery of the interference of light with itself 1 was forcing natural philosophers to abandon the corpuscular description of light in favor of a wave description devised by Christiaan Huygens—and it was not at all clear how this wave description should be meshed with Newton’s laws of gravity so as to compute the effect of a star’s gravity on the light it emits. For this reason, presumably, Laplace deleted the concept of a dark star from the third and subsequent editions of his book.
O nly in November 1915, after Einstein had formulated his general relativistic laws of gravity, did physicists once again believe they understood gravitation and light well enough to compute the effect of a star’s gravity on the light it emits. Only then could they return with confidence to the dark stars (black holes) of Michell and Laplace.
The first step was made by Karl Schwarzschild, one of the most distinguished astrophysicists of the early twentieth century. Schwarz-schild, then serving in the German army on the Russian front of World War I, read Einstein’s formulation of general relativity in the 25 November 1915 issue of the Proceedings of the Prussian Academy of Sciences. Almost immediately he set out to discover what predictions Einstein’s new gravitation laws might make about stars.
Since it would be very complicated, mathematically, to analyze a star that spins or is nonspherical, Schwarzschild confined himself to stars that do not spin at all and that are precisely spherical, and to ease his calculations, he sought first a mathematical description of the star’s exterior and delayed its interior until later. Within a few days he had the answer. He had calculated, in exact detail, from Einstein’s new field equation, the curvature of spacetime outside any spherical, non-spinning star. His calculation was elegant and beautiful, and the curved spacetime geometry that it predicted, the Schwarzschild geometry as it soon came to be known, was destined to have enormous impact on our understanding of gravity and the Universe.
Schwarzschild mailed to Einstein a paper describing his calculations, and Einstein presented it in his behalf at a meeting of the Prussian Academy of Sciences in Berlin on 13 January 1916. Several weeks later, Einstein presented the Academy a second paper by Schwarzschild: an exact computation of the spacetime curvature inside the star. Only four months later, Schwarzschild’s remarkable productivity was halted: On 19 June, Einstein had the sad task of reporting to the Academy that Karl Schwarzschild had died of an illness contracted on the Russian front.
T he Schwarzschild geometry is the first concrete example of spacetime curvature that we have met in this book. For this reason, and because it is so central to the properties of black holes, we shall examine it in detail.
If we had been thinking all our lives about space and time as an absolute, unified, four-dimensional spacetime “fabric,” then it would be appropriate to describe the Schwarzschild geometry immediately in the language of curved (warped), four-dimensional spacetime. However, our everyday experience is with three-dimensional space and one-dimensional time, un-unified; therefore, I shall give a description in which warped spacetime is split up into warped space plus warped time.
Karl Schwarzschild in his academic robe in Göttingen, Germany. [Courtesy AIP Emilio Segré Visual Archives.]
Since space and time are “relative” (my space differs from your space and my time from yours, if we are moving relative to each other 2 ), such a split requires first choosing a reference frame—that is, choosing a state of motion. For a star, there is a natural choice, one in which the star is at rest; that is, the star’s own. reference frame. In other words, it is natural to examine the star’s own space and the star’s own time rather than the space and time of someone moving at high speed through the star.
As an aid in visualizing the curvature (warpage) of the star’s space, I shall use a drawing called an embedding diagram Because embedding diagrams will play a major role in future chapters, I shall introduce the concept carefully, with the help of an analogy.
Imagine a family of human-like creatures who live in a universe with only two spatial dimensions. Their universe is the curved, bowl-like surface depicted in Figure 3.2. They, like their universe, are two-dimensional; they are infinitesimally thin perpendicular to the surface. Moreover, they cannot see out of the surface; they see by means of light rays that move in the surface and never leave it. Thus, these “2D beings,” as I shall call them, have no method whatsoever to get any information about anything outside their two-dimensional universe.
These 2D beings can explore the geometry of their two-dimensional universe by making measurements on straight lines, triangles, and circles. Their straight lines are the “geodesics” discussed in Chapter 2 (Figure 2.4 and associated text): the straightest lines that exist in their two-dimensional universe. In the bottom of their universe’s “bowl,” which we see in Figure 3.2 as a segment of a sphere, their straight lines are segments of great circles like the equator of the Earth or its lines of constant longitude. Outside the lip of the bowl their universe is flat, so their straight lines are what we would recognize as ordinary straight lines.
If the 2D beings examine any pair of parallel straight lines in the outer, flat part of their universe (for example, Lt and L2 of Figure 3.2), then no matter how far the beings follow those lines, they will never see them cross. In this way, the beings discover the flatness of the outer region. On the other hand, if they construct the parallel straight lines L3 and L4 outside the bowl’s lip, and then follow those lines into the bowl region, keeping them always as straight as possible (keeping them geodesics), they will see the lines cross at the bottom of the bowl. In this way, they discover that the inner, bowl region of their universe is curved.
The 2D beings can also discover the flatness of the outer region and the curvature of the inner region by measuring circles and triangles (Figure 3.2). In the outer region, the circumferences of all circles are equal to π (3.14159265 . . .) times their diameters. In the inner region, circumferences of circles are less than π times their diameters; for example, the large circle drawn near the bowl’s bottom in Figure 3.2 has a circumference equal to 2.5 times its diameter. When the 2D beings construct a triangle whose sides are straight lines (geodesics) and then add up the triangle’s interior angles, they obtain 180 degrees in the outer, flat region, and more than 180 degrees in the inner, curved region.
Having discovered, by such measurements, that their universe is curved, the 2D beings might begin to speculate about the existence of a three-dimensional space in which their universe resides—in which it is embedded. They might give that three-dimensional space the name hyperspace, and speculate about its properties; for example, they might presume it to be “flat” in the Euclidean sense that straight, parallel lines in it never cross. You and I have no difficulty visualizing such a hyperspace; it is the three-dimensional space of Figure 3.2, the space of our everyday experience. However, the 2D beings, with their limited two-dimensional experience, would have great difficulty visualizing it. Moreover, there is no way that they could ever learn whether such a hyperspace really exists. They can never get out of their two-dimensional universe and into hyperspace’s third dimension, and because they see only by means of light rays that stay always in their universe, they can never see into hyperspace. For them, hyperspace would be entirely hypothetical.
3.2 A two-dimensional universe peopled by 2D beings.
The third dimension of hyperspace has nothing to do with the 2D beings’ “time” dimension, which they might also think of as a third dimension. When thinking about hyperspace, the beings would actually have to think in terms of four dimensions: two for the space of their universe, one for its time, and one for the third dimension of hyperspace.
W e are three-dimensional beings, and we live in a curved three-dimensional space. If we were to make measurements of the geometry of our space inside and near a star—the Schwarzschild geometry- —we would discover it to be curved in a manner closely analogous to that of the 2D beings’ universe.
We can speculate about a higher-dimensional, flat hyperspace in which our curved, three-dimensional space is embedded. It turns out that such a hyperspace must have six dimensions in order to accommodate curved three-dimensional spaces like ours inside itself. (And when we remember that our Universe also has a time dimension, we must think in terms of seven dimensions in all.)
Now, it is even harder for me to visualize our three-dimensional space embedded in a six-dimensional hyperspace than it would be for 2D beings to visualize their two-dimensional space embedded in a three-dimensional hyperspace. However, there is a trick that helps enormously, a trick depicted in Figure 3.3.
Figure 3.3 shows a thought experiment: A thin sheet of material is inserted through a star in its equatorial plane (upper left), so the sheet bisects the star leaving precisely identical halves above and below it. Even though this equatorial sheet looks flat in the picture, it is not really flat. The star’s mass warps three-dimensional space inside and around the star in a manner that the upper left picture cannot convey, and that warpage curves the equatorial sheet in a manner the picture does not show. We can discover the sheet’s curvature by making geometric measurements on it in our real, physical space, in precisely the same way as the 2D beings make measurements in the two-dimensional space of their universe. Such measurements will reveal that straight lines which are initially parallel cross near the star’s center, the circumference of any circle inside or near the star is less than π times its diameter, and the sums of the internal angles of triangles are greater than 180 degrees. The details of these curved-space distortions are predicted by Schwarzschild’s solution of Einstein’s equation.
To aid in visualizing this Schwarzschild curvature, we, like the 2D beings, can imagine extracting the equatorial sheet from the curved, three-dimensional space of our real Universe, and embedding it in a fictitious, flat, three-dimensional hyperspace (lower right in Figure 3.3). In the uncurved hyperspace, the sheet can maintain its curved geometry only by bending downward like a bowl. Such diagrams of two-dimensional sheets from our curved Universe, embedded in a hypothetical, flat, three-dimensional hyperspace, are called embedding diagrams.
3.3 The curvature of the three-dimensional space inside and around a star (upper left), as depicted by means of an embedding diagram (lower right). This is the curvature predicted by Schwarzschild’s solution to Einstein’s field equation.
It is tempting to think of hyperspace’s third dimension as being the same as the third spatial dimension of our own Universe. We must avoid this temptation. Hyperspace’s third dimension has nothing whatsoever to do with any of the dimensions of our own Universe. It is a dimension into which we can never go and never see, and from which we can never get any information; it is purely hypothetical. Nonetheless, it is useful. It helps us visualize the Schwarzschild geometry, and later in this book it will help us visualize other curved-space geometries: those of black holes, gravitational waves, singularities, and worm-holes (Chapters 6, 7, 10, 13, and 14).
As the embedding diagram in Figure 3.3 shows, the Schwarzschild geometry of the star’s equatorial sheet is qualitatively the same as the geometry of the 2D beings’ universe: Inside the star, the geometry is bowl-like and curved; far from the star it becomes flat. As with the large circle in the 2D beings’ bowl (Figure 3.2), so also here (Figure 3.3), the star’s circumference divided by its diameter is less than π. For our Sun, the ratio of circumference to diameter is predicted to be less than π by several parts in a million; in other words, inside the Sun, space is flat to within several parts in a million. However, if the Sun kept its same mass and were made smaller and smaller in circumference, then the curvature inside it would become stronger and stronger, the downward dip of the bowl in the embedding diagram of Figure 3.3 would become more and more pronounced, and the ratio of circumference to diameter would become substantially less than π.
Because space is different in different reference frames (“your space is a mixture of my space and my time, if we move relative to each other”), the details of the star’s spatial curvature will be different as measured in a reference frame that moves at high speed relative to the star than as measured in a frame where the star is at rest. In the space of the high-speed reference frame, the star is somewhat squashed perpendicular to its direction of motion, so the embedding diagram looks much like that of Figure 3.3, but with the bowl compressed transversely into an oblong shape. This squashing is the curved-space variant of the contraction of space that Fitzgerald discovered in a universe without gravity (Chapter 1 ).
Schwarzschild’s solution to the Einstein field equation describes not only this curvature (or warpage) of space, but also a warpage of time near the star—a warpage produced by the star’s strong gravity. In a reference frame that is at rest with respect to the star, and not flying past it at high speed, this time warpage is precisely the gravitational time dilation discussed in Chapter 2 (Box 2.4 and associated discussion): Near the star’s surface, time flows more slowly than far away, and at the star’s center, it flows slower still.
In the case of the Sun, the time warpage is small: At the Sun’s surface, time should flow more slowly by just 2 parts in a million (64 seconds in one year) than far from the Sun, and at the Sun’s center it should flow more slowly than far away by about 1 part in 100,000 (5 minutes in one year). However, if the Sun kept its same mass and were made smaller in circumference so its surface was closer to its center, then its gravity would be stronger, and correspondingly its gravitational time dilation—its warpage of time—would become larger.
One consequence of this time warpage is the gravitational redshift of light emitted from a star’s surface. Since the light’s frequency of oscillation is governed by the flow of time at the place where the light is emitted, light emerging from atoms on the star’s surface will have a lower frequency when it reaches Earth than light emitted by the same kinds of atoms in interstellar space. The frequency will be lowered by precisely the same amount as the flow of time is slowed. A lower frequency means a longer wavelength, so light from the star must be shifted toward the red end of the spectrum by the same amount as time is dilated on the star’s surface.
At the Sun’s surface the time dilation is 2 parts in a million, so the gravitational redshift of light arriving at the Earth from the Sun should also be 2 parts in a million. This was too small a redshift to be measured definitively in Einstein’s day, but in the early 1960s, technology began to catch up with Einstein’s laws of gravity: Jim Brault of Princeton University, in a very delicate experiment, measured the red-shift of the Sun’s light, and obtained a result in nice agreement with Einstein’s prediction.
W ithin a few years after Schwarzschild’s untimely death, his spacetime geometry became a standard working tool for physicists and astrophysicists. Many people, including Einstein, studied it and computed its implications. All agreed and took seriously the conclusion that, if the star were rather large in circumference, like the Sun, then spacetime inside and around it should be very slightly curved, and light emitted from its surface and received at Earth should be shifted in color, ever so slightly, toward the red. All also agreed that the more compact the star, the greater must be the warpage of its spacetime and the larger the gravitational redshift of light from its surface. However, few were willing to take seriously the extreme predictions that the Schwarzschild geometry gave for highly compact stars (Figure 3.4):
The Schwarzschild geometry predicted that for each star there is a critical circumference, which depends on the star’s mass—the same critical circumference as had been discovered by John Michell and Pierre Simon Laplace more than a century earlier: 18.5 kilometers times the mass of the star in units of the mass of the Sun. If the star’s actual circumference is larger than this critical one by a factor of 4 (upper part of Figure 3.4), then the star’s space will be moderately curved as shown, time at its surface will flow 15 percent more slowly than far away, and light emitted from its surface will be shifted toward the red end of the spectrum by 15 percent. lf the star’s circumference is smaller, just twice the critical one (middle part of Figure 3.4), its space will be more strongly curved, time at its surface will flow 41 percent more slowly than far away, and light from its surface will be redshifted by 41 percent. These predictions seemed acceptable and reasonable. What did not seem at all reasonable to physicists and astrophysicists of the 1920s, or even as late as the 1960s, was the prediction for a star whose actual circumference was the same as its critical one (bottom part of Figure 3.4). For such a star, with its more strongly curved space, the flow of time at the star’s surface is infinitely dilated; time does not flow at all—it is frozen. And correspondingly, no matter what may be the color of light when it begins its journey upward from the star’s surface, it must get shifted beyond the red, beyond the infrared, beyond. radio wavelengths, all the way to infinite wavelengths; that is, all the way out of existence. In modern language, the star’s surface, with its critical circumference, is precisely at the horizon of a black hole; the star, by its strong gravity, is creating a black-hole horizon around itself.
3.4 General relativity’s predictions for the curvature of space and the redshift of light from three highly compact stars with the same mass but different circumferences. The first is four times larger than the critical circumference, the second is twice as large as critical, and the third has its circumference precisely critical. In modern language, the surface of the third star is a black-hole horizon.
The bottom line of this Schwarzschild-geometry discussion is the same as that found by Michell and Laplace: A star as small as the critical circumference must appear completely dark, when viewed from far away; it must be what we now call a black hole. The bottom line is the same, but the mechanism is completely different:
Michell and Laplace, with their Newtonian view of space and time as absolute and the speed of light as relative, believed that for a star just a bit smaller than the critical circumference, corpuscles of light would very nearly escape. They would fly up to great heights above the star, higher than any orbiting planet; but as they climbed, they would be slowed by the star’s gravity, then halted somewhere short of interstellar space, then turned around and pulled back down to the star. Though creatures on an orbiting planet could see the star by its slow-moving light (to them it would not be dark), we, living far away on Earth, could not see it at all. The star’s light could not reach us. For us the star would be totally black.
By contrast, Schwarzschild’s spacetime curvature required that light always propagate with the same universal speed; it can never be slowed. (The speed of light is absolute, but space and time are relative.) However, if emitted from the critical circumference, the light must get shifted in wavelength an infinite amount, while traveling upward an infinitesimal distance. (The wavelength shift must be infinite because the flow of time is infinitely dilated at the horizon, and the wavelength always shifts by the same amount as time is dilated.) This infinite shift of wavelength, in effect, removes all the light’s energy; and the light, thereupon, ceases to exist! Thus, no matter how close a planet might be to the critical circumference, creatures on it cannot see any light at all emerging from the star.
In Chapter 7 , we shall study how the light behaves as seen from inside a black hole’s critical circumference, and shall discover that it does not cease to exist after all. Rather, it simply is unable to escape the critical circumference (the hole’s horizon) even though it is moving outward at the standard, universal speed of 299,792 kilometers per second. But this early in the book, we are not yet ready to comprehend such seemingly contradictory behavior. We must first build up our understanding of other things, as did physicists during the decades between 1916 and 1960.
D uring the 1920s and into the 1930s, the world’s most renowned experts on general relativity were Albert Einstein and the British astrophysicist Arthur Eddington. Others understood relativity, but Einstein and Eddington set the intellectual tone of the subject. And, while a few others were willing to take black holes seriously, Einstein and Eddington were not. Black holes just didn’t “smell right”; they were outrageously bizarre; they violated Einstein’s and Eddington’s intuitions about how our Universe ought to behave.
In the 1920s Einstein seems to have dealt with the issue by ignoring it. Nobody was pushing black holes as a serious prediction, so there was not much need on that score to straighten things out. And since other mysteries of nature were more interesting and puzzling to Einstein, he put his energies elsewhere.
Eddington in the 1920s took a more whimsical approach. He was a bit of a ham, he enjoyed popularizing science, and so long as nobody was taking black holes too seriously, they were a playful thing to dangle in front of others. Thus, we find him writing in 1926 in his book The Internal Constitution of the Stars that no observable star can possibly be more compact than the critical circumference: “Firstly,” he wrote, “the force of gravitation would be so great that light would be unable to escape from it, the rays falling back to the star like a stone to the Earth. Secondly, the redshift of the spectral lines would be so great that the spectrum would be shifted out of existence. Thirdly, the mass would produce so much curvature of the space-time metric that space would close up round the star, leaving us outside (i.e. nowhere).” The first conclusion was the Newtonian version of light not escaping; the second was a semi-accurate, relativistic description; and the third was typical Eddingtonian hyperbole. As one sees clearly from the embedding diagrams of Figure 3.4, when a star is as small as the critical circumference, the curvature of space is strong but not infinite, and space is definitely not wrapped up around the star. Eddington may have known this, but his description made a good story, and it captured in a whimsical way the spirit of Schwarzschild’s spacetime curvature.
In the 1930s, as we shall see in Chapter 4 , the pressure to take black holes seriously began to mount. As the pressure mounted, Eddington, Einstein, and others among the “opinion setters” began to express unequivocal opposition to these outrageous objects.
In 1939, Einstein published a general relativistic calculation that he interpreted as an example of why black holes cannot exist. His calculation analyzed the behavior of an idealized kind of object which one might have thought could be used to make a black hole. The object was a cluster of particles that pull on each other gravitationally and thereby hold the cluster together, in much the same way as the Sun holds the solar system together by pulling gravitationally on its planets. The particles in Einstein’s cluster all moved in circular orbits around a common center; their orbits formed a sphere, with particles on one side of the sphere pulling gravitationally on those on the other side (left half of Figure 3.5).
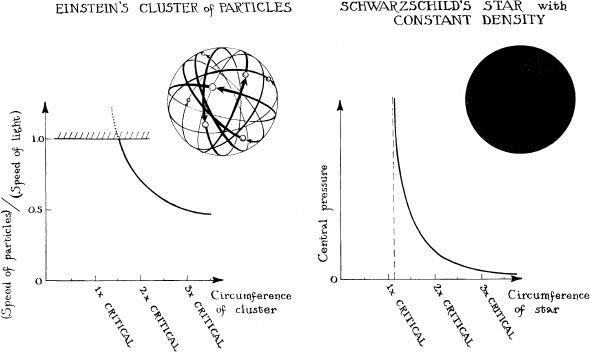
3.5 Einstein’s evidence that no object can ever be as small as its critical circumference. Left: If Einstein’s spherical cluster of particles is smaller than 1.5 critical circumferences, then the particles’ speeds must exceed the speed of light, which is impossible. Right: If a star with constant density is smaller than 9/8 = 1.125 critical circumferences, then the pressure at the star’s center must be infinite, which is impossible.
Einstein imagined making this cluster smaller and smaller, trying to drive its actual circumference down toward the critical circumference. As one might expect, his calculation showed that the more compact the cluster, the stronger the gravity at its spherical surface and the faster the particles must move on its surface to prevent themselves from being pulled in. If the cluster were smaller than 1.5 times the critical circumference, Einstein’s calculations showed, then its gravity would be so strong that the particles would have to move faster than the speed of light to avoid being pulled in. Since nothing can move faster than light, there was no way the cluster could ever be smaller than 1.5 times critical. “The essential result of this investigation,” Einstein wrote, “is a clear understanding as to why the ‘Schwarzschild singularities’ do not exist in physical reality.”
As backing for his view, Einstein could also appeal to the internal structure of an idealized star made of matter whose density is constant throughout the stellar interior (right half of Figure 3.5). Such a star was prevented from imploding by the pressure of the gas inside it. Karl Schwarzschild had used general relativity to derive a complete mathematical description of such a star, and his formulas showed that, if one makes the star more and more compact, then in order to counteract the increased strength of its internal gravity, the star’s internal pressure must rise higher and higher. As the star’s shrinking circumference nears 
= 1.125 times its critical circumference, Schwarzschild’s formulas show the central pressure becoming infinitely large. Since no real gas can ever produce a truly infinite pressure (nor can any other kind of matter), such a star could never get as small as 1.125 times critical, Einstein believed.
Einstein’s calculations were correct, but his reading of their message was not. The message he extracted, that no object can ever become as small as the critical circumference, was determined more by Einstein’s intuitive opposition to Schwarzschild singularities (black holes) than by the calculations themselves. The correct message, we now know in retrospect, was this:
Einstein’s cluster of particles and the constant-density star could never be so compact as to form a black hole because Einstein demanded that some kind of force inside them counterbalance the squeeze of gravity: the force of gas pressure in the case of the star; the centrifugal force due to the particles’ motions in the case of the cluster. In fact, it is true that no force whatsoever can resist the squeeze of gravity when an object is very near the critical circumference. But this does not mean the object can never get so small. Rather, it means that, if the object does get that small, then gravity necessarily overwhelms all other forces inside the object, and squeezes the object into a catastrophic implosion, which forms a black hole. Since Einstein’s calculations did not include the possibility of implosion (he left it out of all his equations), he missed this message.
We are so accustomed to the idea of black holes today that it is hard not to ask, “How could Einstein have been so dumb? How could he leave out the very thing, implosion, that makes black holes?” Such a reaction displays our ignorance of the mindset of nearly everybody in the 1920s and 1930s.
General relativity’s predictions were poorly understood. Nobody realized that a sufficiently compact object must implode, and that the implosion will produce a black hole. Rather, Schwarzschild singularities (black holes) were imagined, incorrectly, to be objects that are hovering at or just inside their critical circumference, supported against gravity by some sort of internal force; Einstein therefore thought he could debunk black holes by showing that nothing supported by internal forces can be as small as the critical circumference.
If Einstein had suspected that “Schwarzschild singularities” can really exist, he might well have realized that implosion is the key to forming them and internal forces are irrelevant. But he was so firmly convinced they cannot exist (they “smelled wrong”; terribly wrong) that he had an impenetrable mental block against the truth—as did nearly all his colleagues.
I n T. H. White’s epic novel The Once and Future King there is a society of ants which has the motto, “Everything not forbidden is compulsory.” That is not how the laws of physics and the real Universe work. Many of the things permitted by the laws of physics are so highly improbable that in practice they never happen. A simple and time-worn example is the spontaneous reassembly of a whole egg from fragments splattered on the floor: Take a motion picture of an egg as it falls to the floor and splatters into fragments and goo. Then run the motion picture backward, and watch the egg spontaneously regenerate itself and fly up into the air. The laws of physics permit just such a regeneration with time going forward, but it never happens in practice because it is highly improbable.
Physicists’ studies of black holes during the 1920s and 1930s, and even on into the 1940s and 1950s, dealt only with the issue of whether the laws of physics permit such objects to exist—and the answer was equivocal: At first sight, black holes seemed to be permitted; then Einstein, Eddington, and others gave (incorrect) arguments that they are forbidden. In the 1950s, when those arguments were ultimately disproved, many physicists turned to arguing that black holes might be permitted by the laws of physics, but are so highly improbable that (like the reassembling egg) they never occur in practice.
In reality, black holes, unlike the reassembling egg, are compulsory in certain common situations; but only in the late 1960s, when the evidence that they are compulsory became overwhelming, did most physicists begin to take black holes seriously. In the next three chapters I shall describe how that evidence mounted from the 1930s through the 1960s, and the widespread resistance it met.
T his widespread and almost universal twentieth-century resistance to black holes is in marked contrast to the enthusiasm with which black holes were met in the eighteenth-century era of John Michell and Pierre Simon Laplace. Werner Israel, a modern-day physicist at the University of Alberta who has studied the history in depth, has speculated on the reasons for this difference.
“I am sure [that the eighteenth-century acceptance of black holes] was not just a symptom of the revolutionary fervour of the 1790s,” Israel writes. “The explanation must be that Laplacian dark stars [black holes] posed no threat to our cherished faith in the permanence and stability of matter. By contrast, twentieth-century black holes are a great threat to that faith.”
Michell and Laplace both imagined their dark stars as made from matter with about the same density as water or earth or rock or the Sun, about 1 gram per cubic centimeter. With this density, a star, to be dark (to be contained within its critical circumference), must have a mass about 140 million times greater than the Sun’s and a circumference about 3 times larger than the Earth’s orbit. Such stars, governed by Newton’s laws of physics, might be exotic, but they surely were no threat to any cherished beliefs about nature. If one wanted to see the star, one need only land on a planet near it and look at its light corpuscles as they rose in their orbits, before plummeting back to the star’s surface. If one wanted a sample of the material from which the star was made, one need only fly down to the star’s surface, scoop some up, and bring it back to Earth for laboratory study. I do not know whether Michell, Laplace, or others of their day speculated about such things, but it is clear that if they did, there was no reason for concern about the laws of nature, about the permanence and stability of matter.
The critical circumference (horizon) of a twentieth-century black hole presents quite a different challenge. At no height above the horizon can one see any emerging light. Anything that falls through the horizon can never thereafter escape; it is lost from our Universe, a loss that poses a severe challenge to physicists’ notions about the conservation of mass and energy.
“There is a curious parallel between the histories of black holes and continental drift [the relative drifting motion of the Earth’s continents],” Israel writes. “Evidence for both was already non-ignorable by 1916, but both ideas were stopped in their tracks for half a century by a resistance bordering on the irrational. I believe the underlying psychological reason was the same in both cases. Another coincidence: resistance to both began to crumble around 1960. Of course, both fields [astrophysics and geophysics] benefitted from postwar technological developments. But it is nonetheless interesting that this was the moment when the Soviet H-bomb and Sputnik swept away the notion of Western science as engraved in stone and beyond challenge, and, perhaps, instilled the suspicion that there might be more in heaven and earth than Western science was prepared to dream of.”
1. Chapter 10 .
2. Figure 1.3, and the lessons of the tale of Mledina and Serona in Chapter 2 .
The Mystery of the White Dwarfs
in which Eddington and Chandrasekhar do battle
over the deaths of massive stars;
must they shrink when they die,
creating black holes?
or will quantum mechanics save them?
T he year was 1928; the place, southeast India, the city of Madras on the Bay of Bengal. There, at Presidency College, a seventeen-year-old Indian boy named Subrahmanyan Chandrasekhar was immersed in the study of physics, chemistry, and mathematics. Chandrasekhar was tall and handsome, with regal bearing and pride in his academic achievements. He had recently read Arnold Sommerfeld’s classic textbook Atomic Structure and Spectral Lines and was now overjoyed that Sommerfeld, one of the world’s great theoretical physicists, had come from his home in Munich to visit Madras.
Eager for personal contact, Chandrasekhar went to Sommerfeld’s hotel room and asked for an interview. Sommerfeld granted an appointment for several days hence.
On the day of his appointment Chandrasekhar, filled with pride and confidence in his mastery of modern physics, walked up to Sommerfeld’s hotel room and knocked on the door. Sommerfeld greeted him politely, inquired about his studies, then deflated him. “The physics you have been studying is a thing of the past. Physics has all changed in the five years since my textbook was written,” he explained. He went on to describe a revolution in physicists’ understanding of the laws that govern the realm of the small: the realm of atoms, molecules, electrons, and protons. In this realm, the Newtonian laws had been found to fail in ways that relativity had not anticipated. Their replacement was a radically new set of physical laws—laws that were called quantum mechanics 1 because they deal with the behavior (the “mechanics”) of particles of matter (“quanta”). Though only two years old, the new quantum mechanical laws were already having great success in explaining how atoms and molecules behave.
Chandrasekhar had read in Sommerfeld’s book about the first, tentative version of the new laws. But the tentative quantum laws had been unsatisfactory, Sommerfeld explained to him. Although they agreed well with experiments on simple atoms and molecules such as hydrogen, the tentative laws could not account for the behaviors of more complicated atoms and molecules, and they did not mesh in a logically consistent way with each other or with the other laws of physics. They were little more than a mishmash of unaesthetic, ad-hoc rules of computation.
The new version of the laws, though radical in form, looked far more promising. It explained complicated atoms and complicated molecules, and it seemed to be meshing quite nicely with the rest of physics.
Chandrasekhar listened to the details, entranced.
Quantum Mechanics and the Guts of White Dwarfs
W hen they parted, Sommerfeld gave Chandrasekhar the galley proofs of a technical article that he had just written. It contained a derivation of the quantum mechanical laws that govern large collections of electrons squeezed together into small volumes, in a metal for instance.
Chandrasekhar read Sommerfeld’s galley proofs with fascination, understood them, and then spent many days in the University library studying all the research articles he could find relating to them. Especially interesting was an article entitled “On Dense Matter” by the English physicist R. H. Fowler, published in the 10 December 1926 issue of Monthly Notices of the Royal Astronomical Society. Fowler’s article pointed Chandrasekhar to a most fascinating book, The Internal Constitution of the Stars, by the eminent British astrophysicist Arthur S. Eddington, in which Chandrasekhar found a description of the mystery of white-dwarf stars.
“White dwarfs were a type of star that astronomers had discovered through their telescopes. The mysterious thing about white dwarfs was the extremely high density of the matter inside them, a density far greater than humans had ever before encountered. Chandrasekhar had no way of knowing it when he opened Eddington’s book, but the struggle to unravel the mystery of this high density would ultimately force him and Eddington to confront the possibility that massive stars, when they die, might shrink to form black holes.
“White dwarfs are probably very abundant,” Chandrasekhar read in Eddington’s book. “Only three are definitely known, but they are all within a small distance of the Sun.... The most famous of these stars is the Companion of [the ordinary star] Sirius,” which has the name Sirius B. Sirius and Sirius B are the sixth and seventh nearest stars to the Earth, 8.6 light-years away, and Sirius is the brightest star in our sky. Sirius B orbits Sirius just as the Earth orbits the Sun, but Sirius B requires 50 years to complete an orbit, the Earth only one.
Eddington described how astronomers had estimated, from telescopic observations, the mass and circumference of Sirius B. The mass was that of 0.85 Sun; the circumference, 118,000 kilometers. This meant that the mean density of Sirius B was 61,000 grams per cubic centimeter—61,000 times greater density than water and just about a ton to the cubic inch. “This argument has been known for some years,” Eddington wrote. “I think it has generally been considered proper to add the conclusion ‘which is absurd.’ “ Most astronomers could not take seriously a density so much greater than ever encountered on Earth—and had they known the real truth, as revealed by more modern astronomical observations Ca mass of 1.05 Suns, a circumference of 31,000 kilometers, and a density of 4 million grams per cubic centimeter or 60 tons per cubic inch), they would have considered it even more absurd; see Figure 4.1.
Eddington went on to describe a key new observation that reinforced the “absurd” conclusion. If Sirius B were, indeed, 61,000 times denser than water, then according to Einstein’s laws of gravity, light climbing out of its intense gravitational field would be shifted to the red by 6 parts in 100,000—a shift 30 times greater than for light emerging from the Sun, and therefore easier to measure. This redshift prediction, it seemed, had been tested and verified just before Eddington’s book went to press in 1925, by the astronomer W. S. Adams at Mount Wilson Observatory on a mountaintop above Pasadena, California. 2 “Professor Adams has killed two birds with one stone,” Eddington wrote; “he has carried out a new test of Einstein’s general theory of relativity and he has confirmed our suspicion that matter 2000 times denser than platinum is not only possible, but is actually present in the Universe.”
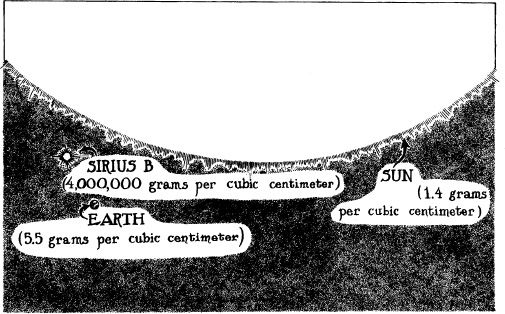
4.1 Comparison of the sizes and mean densities of the Sun, the Earth, and the white-dwarf star Sirius B, using modern values.
Further on in Eddington’s book, Chandrasekhar found a description of how the internal structure of a star, such as the Sun or Sirius B, is governed by the balance of internal pressure against gravitational squeeze. This squeeze/pressure balance can be understood (though this was not Eddington’s way) by analogy with squeezing a balloon in your hands (left half of Figure 4.2): The inward force of your squeezing hands is precisely counterbalanced by the outward force of the balloon’s air pressure—air pressure that is created by air molecules inside the balloon bombarding the balloon’s rubber wall.
4.2 Left: The balance between the squeeze of your hands and the pressure inside a balloon. Right: The analogous balance between the gravitational squeeze (weight) of an outer shell of stellar matter and the pressure of an inner ball of stellar matter.
For a star (right half of Figure 4.2) the analogue of your squeezing hands is the weight of an outer shell of stellar matter, and the analogue of the air in the balloon is the spherical ball of matter inside that shell. The boundary between the outer shell and inner ball can be chosen anywhere one wishes—a meter deep into the star, a kilometer deep, a thousand kilometers deep. Wherever one chooses the boundary, it must fulfill the requirement that the weight of the outer shell squeezing on the inner ball (the outer shell’s “gravitational squeeze”) is precisely counterbalanced by the pressure of the inner ball’s molecules bombarding the outer shell. This balance, enforced at each and every location inside the star, determines the star’s structure,. that is, it determines the details of how the star’s pressure, gravity, and density vary from the star’s surface down to its center.
Eddington’s book also described a troubling paradox in what was then known about the structures of white-dwarf stars. Eddington believed—indeed all astronomers believed in 1925—that the pressure of white-dwarf matter, like that in your balloon, must be caused by its heat. Heat makes the matter’s atoms fly about inside the star at high speed, bombarding each other and bombarding the interface between the star’s outer shell and its inner ball. If we take a “macroscopic” viewpoint, too coarse to detect the individual atoms, then all we can measure is the total bombardment force of all the atoms that hit, say, one square centimeter of the interface. That total force is the star’s pressure.
As the star cools by emitting radiation into space, its atoms will fly about more slowly, their pressure will go down, and the weight of the star’s outer shell will then squeeze its inner ball into a smaller volume. This compression of the ball, however, heats it up again, raising its pressure so a new squeeze/pressure balance can be achieved—one with the star slightly smaller than before. Thus, as Sirius B continues gradually to cool by radiating heat into interstellar space, it must gradually shrink in size.
How does this gradual shrinkage end? What will be the ultimate fate of Sirius B? The most obvious (but wrong) answer, that the star will shrink until it is so small that it becomes a black hole, was anathema to Eddihgton; he refused even to consider it. The only reasonable answer, he asserted, was that the star must ultimately turn cold and then support itself not by thermal pressure (that is, heat-induced pressure), but rather by the only other type of pressure known in 1925: the pressure that one finds in solid objects like rocks, a pressure due to repulsion between adjacent atoms. But such “rock pressure” was only possible, Eddington believed (incorrectly), if the star’s matter has a density something like that of a rock, a few grams per cubic centimeter—10,000 times less than the present density of Sirius B.
This line of argument led to Eddington’s paradox. In order to reexpand to the density of rock and thereby be able to support itself when it turns cold, Sirius B would have to do enormous work against its own gravity, and physicists did not know of any energy supply inside the star adequate for such work. “Imagine a body continually losing heat but with insufficient energy to grow cold!” Eddington wrote. “It is a curious problem and one may make many fanciful suggestions as to what actually will happen. We here leave aside the difficulty as not necessarily fatal.”
Chandrasekhar had found the resolution of this 1925 paradox in R. H. Fowler’s 1926 article “On Dense Matter.” The resolution lay in the failure of the laws of physics that Eddington used. Those laws had to be replaced by the new quantum mechanics, which described the pressure inside Sirius B and other white dwarfs as due not to heat, but instead to a new, quantum mechanical phenomenon: the degenerate motions of electrons, also called electron degeneracy. 3
E lectron degeneracy is somewhat like human claustrophobia. When matter is squeezed to a density 10,000 times higher than that of rock, the cloud of electrons around each of its atomic nuclei gets squashed 10,000-fold. Each electron thereby gets confined to a “cell” with 10,000 times smaller volume than the one it previously was allowed to move around in. With so little space available to it, the electron, like a claustrophobic human, starts to shake uncontrollably. It flies about its tiny cell at high speed, kicking with great force against adjacent electrons in their cells. This degenerate motion, as physicists call it, cannot be stopped by cooling the matter. Nothing can stop it; it is forced on the electron by the laws of quantum mechanics, even when the matter is at absolute zero temperature.
This degenerate motion is a consequence of a feature of matter that Newtonian physicists never dreamed of, a feature called wave/particle duality: Every kind of particle, according to quantum mechanics, sometimes behaves like a wave, and every kind of wave sometimes behaves like a particle. Thus, waves and particles are really the same thing, a “thing” that sometimes behaves like a wave and sometimes like a particle; see Box 4.1.
Electron degeneracy is easily understood in terms of wave/particle duality. When matter is compressed to high densities, and each electron inside the matter gets confined to an extremely small cell squeezed up against neighboring electrons’ cells, the electron begins to behave in part like a wave. The wavelength of the electron wave (the distance between its crests) cannot be larger than the electron’s cell; if it were, the wave would extend beyond the cell. Now, particles with very short wavelengths are necessarily highly energetic. (A common example is the particle associated with an electromagnetic wave, the photon. An X-ray photon has a wavelength far shorter than that of a photon of light, and as a result X-ray photons are far more energetic than photons of light. Their higher energies enable the X-ray photons to penetrate human flesh and bone.)
In the case of an electron inside very dense matter, the electron’s short wavelength and accompanying high energy imply rapid motion, and this means that the electron must fly around inside its cell, behaving like an erratic, high-speed mutant: half particle, half wave. Physicists say that the electron is “degenerate,” and they call the pressure that its erratic high speed motion produces “electron degeneracy pressure.” There is no way to get rid of this degeneracy pressure; it is an inevitable consequence of confining the electron to such a small cell. Moreover, the higher the matter’s density, the smaller the cell, the shorter the electron wavelength, the higher the electron energy, the faster the electron’s motion, and thus the larger its degeneracy pressure. In ordinary matter with ordinary densities, the degeneracy pressure is so tiny that one never notices it, but at the huge densities of white dwarfs it is enormous.
Box 4.1
A Brief History of Wave/Particle Duality
Already in Isaac Newton’s time (the late 1600s), physicists were struggling over the issue of whether light is made of particles or waves. Newton, though equivocal about the issue, leaned toward particles and called them corpuscles, while Christiaan Huygens argued for waves. Newton’s particle view prevailed until the early 1800s, when the discovery that light can interfere with itself (Chapter 10 ) converted physicists to Huygens’ wave viewpoint. In the mid-1800s, James Clerk Maxwell put the wave description on a firm footing with his unified laws of electricity and magnetism, and physicists then thought the issue had finally been settled. However, that was before quantum mechanics.
In the 1890s Max Planck noticed hints, in the shape of the spectrum of the light emitted by very hot objects, that something might be missing in physicists’ understanding of light. Einstein, in 1905, showed what was missing: Light sometimes behaves like a wave and sometimes like a particle (now called a photon). It behaves like a wave, Einstein explained, when it interferes with itself; but it behaves like a particle in the photoelectric effect: When a dim beam of light shines on a piece of metal, the beam ejects electrons from the metal one at a time, precisely as though individual particles of light (individual photons) were hitting the electrons and knocking them out of the metal’s surface one by one. From the electrons’ energies, Einstein inferred that the photon energy is always inversely proportional to the light’s wavelength. Thus, the photon and wave properties of light are intertwined; the wavelength is inexorably tied to the photon energy. _Einstein’s discovery of the wave/particle duality of light, and the tentative quantum mechanical laws of physics that he began to build around this discovery, won him the 1921 Nobel Prize in 1922.
Although Einstein almost single-handedly formulated general relativity, he was only one among many who contributed to the laws of quantum mechanics—the laws of the “realm of the small.”
When Einstein discovered the wave/particle duality of light, he did not realize that an electron or proton might also behave sometimes like a particle and sometimes like a wave. Nobody recognized it until the mid-1920s when Louis de Broglie raised it as a conjecture and then Erwin Schrödinger used it as a foundation for a full set of quantum mechanical laws, laws in which an electron is a wave of probability. Probability for what? For the location of a particle. These “new” quantum mechanical laws (which have been enormously successful in explaining how T electrons, protons, atoms, and molecules behave) will not concern us much in this book. However, from time to time a few of their features will be important. In this chapter, the important feature is electron degeneracy.
W hen Eddington wrote his book, electron degeneracy had not yet been predicted, and it was not possible to compute correctly how rock or other materials will respond if compressed to the ultra-high densities of Sirius B. With the laws of electron degeneracy in hand such computations were now possible, and they had been conceived and carried out by R. H. Fowler in his 1926 article.
According to Fowler’s computations, because the electrons in Sirius B and other white-dwarf stars have been compressed into such tiny cells, their degeneracy pressure is far larger than their thermal (heat-induced) pressure. Accordingly, when Sirius B cools off, its minuscule thermal pressure will disappear, but its enormous degeneracy pressure will remain and will continue to support it against gravity.
Thus, the resolution of Eddington’s white-dwarf paradox was twofold: (1) Sirius B is not supported against its own gravity primarily by thermal pressure as everyone had thought before the advent of the new quantum mechanics; rather, it is supported primarily by degeneracy pressure. (2) When Sirius B cools off, it need not reexpand to the density of rock in order to support itself; rather, it will continue to be supported quite satisfactorily by degeneracy pressure at its present density of 4 million grams per cubic centimeter.
Chandrasekhar, reading these things and studying their mathematical formulations in the library in Madras, was enchanted. This was his first contact with modern astronomy, and he was finding here, side by side, deep consequences of the two twentieth-century revolutions in physics: Einstein’s general relativity, with its new viewpoints on space and time, was showing up in the gravitational redshift of light from Sirius B; and the new quantum mechanics, with its wave/particle duality, was responsible for Sirius B’s internal pressure. This astronomy was a fertile field in which a young man could make his mark.
As he continued his university studies in Madras, Chandrasekhar explored further the consequences of quantum mechanics for the astronomical Universe. He even wrote a small article on his ideas, mailed it to England to R. H. Fowler, whom he had never met, and Fowler arranged for it to be published.
Finally, in 1930 at age nineteen, Chandrasekhar completed the Indian equivalent of an American bachelor’s degree, and in the last week of July he boarded a steamer bound for far-off England. He had been accepted for graduate study at Cambridge University, the home of his heroes, R. H. Fowler and Arthur Eddington.
The Maximum Mass
Those eighteen days at sea, steaming from Madras to Southampton, were Chandrasekhar’s first opportunity in many months to think quietly about physics without the distraction of formal studies and examinations. The solitude of the sea was conducive to thought, and Chandrasekhar’s thoughts were fertile. So fertile, in fact, that they would help to win him the Nobel Prize, but only fifty-four years later, and only after a great struggle to get them accepted by the world’s astronomical community.
Aboard the steamer, Chandrasekhar let his mind reminisce over white dwarfs, Eddington’s paradox, and Fowler’s resolution. Fowler’s resolution almost certainly had to be correct; there was none other in sight. However, Fowler had not worked out the full details of the balance between degeneracy pressure and gravity in a white-dwarf star, nor had he computed the star’s resulting internal structure—the manner in which its density, pressure, and gravity change as one goes from its surface down to its center. Here was an interesting challenge to help ward off boredom during the long voyage.
As a tool in working out the star’s structure, Chandrasekhar needed to know the answer to the following question: Suppose that white-dwarf matter has already been compressed to some density (for example, a density of a million grams per cubic centimeter). Compress the matter (that is, reduce its volume and increase its density) by an additional 1 percent. The matter will protest against this additional compression by raising its pressure. By what percentage will its pressure go up? Physicists use the name adiabatic index for the percentage increase in pressure that results from a 1 percent additional compression. In this book I shall use the more graphic name resistance to compression or simply resistance. (This “resistance to compression” should not be confused with “electrical resistance”; they are completely different concepts.)
Chandrasekhar worked out the resistance to compression by examining step by step the consequences of a 1 percent increase in the density of white-dwarf matter: the resulting decrease in electron cell size, the decrease in electron wavelength, the increase in electron energy and speed, and finally the increase in pressure. The result was clear: A 1 percent increase in density produced 
of a percent (1.667 percent) increase in pressure. The resistance of white-dwarf matter, therefore, was
.
Many decades before Chandrasekhar’s voyage, astrophysicists had computed the details of the balance of gravity and pressure inside any star whose matter has a resistance to compression that is independent of depth in the star-that is, a star whose pressure and density increase in step with each other, as one moves deeper and deeper into the star, with a 1 percent increase in density always accompanied by the same fixed percentage increase in pressure. The details of the resulting stellar structures were contained in Eddington’s book The Internal Constitution of the Stars,
which Chandrasekhar had brought on board the ship because he treasured it so much. Thus, when Chandrasekhar discovered that white-dwarf matter has a resistance to compression of
, independent of its density, he was pleased. He could now go directly to Eddington’s book to discover the star’s internal structure: the manner in which its density and pressure changed from surface to center.
Among the things that Chandrasekhar discovered, by combining the formulas in Eddington’s book with his own formulas, were the density at the center of Sirius B, 360,000 grams per cubic centimeter (6 tons per cubic inch), and the speed of the electrons’ degeneracy motion there, 57 percent of the speed of light.
This electron speed was disturbingly large. Chandrasekhar, like R. H. Fowler before him, had computed the resistance of white-dwarf matter using the laws of quantum mechanics, but ignoring the effects of relativity. However, when any object moves at almost the speed of light, even a particle obeying the laws of quantum mechanics, the effects of special relativity must become important. At 57 percent of the speed of light, relativity’s effects might not be too terribly big, but a more massive white dwarf with its stronger gravity would require a larger central pressure to support itself, and the random speeds of its electrons would be correspondingly higher. In such a white dwarf the effects of relativity surely could not be ignored. So Chandrasekhar returned to the starting point of his analysis, the calculation of the resistance to compression for white-dwarf matter, vowing to include the effects of relativity this time around.
To include relativity in the computation would require meshing the laws of special relativity with the laws of quantum mechanics—a mesh that the great minds of theoretical physics were only then working out. Alone on the steamer and barely graduated from university, Chandrasekhar could not produce that full mesh. However, he was able to produce enough to indicate the principal effects of high electron speeds.
Quantum mechanics insists that when already dense matter is compressed a bit, making each electron’s cell smaller than it was, the electron’s wavelength must decrease and correspondingly the energy of its degeneracy motion must increase. However, Chandrasekhar realized, the nature of the additional electron energy is different, depending on whether the electron is moving slowly compared to light or at close to light speed. If the electron’s motion is slow, then, as in everyday life, an increase of energy means more rapid motion, that is, higher speed. If the electron is already moving at close to light speed, however, there is no way its speed can go up much (if it did, it would exceed the speed limit!), so the energy increase takes a different form, one unfamiliar in everyday life: The additional energy goes into inertia; that is, it increases the electron’s resistance to being speeded up-it makes the electron behave as though it had become a bit heavier. These two different fates of the added energy (added speed versus added inertia) produce different increases in the electron’s pressure, and thus different resistances to compression, Chandrasekhar deduced: at low electron speeds, a resistance of
the same as he had computed before; at high speeds, a resistance of 
.
By combining his
resistance for relativistically degenerate matter
(that is, matter so dense that the degenerate electrons move at nearly the speed of light) with the formulas given in Eddington’s book, Chandrasekhar then deduced the properties of high-density, high-mass white dwarfs. The answer was astonishing: The high-density matter would have difficulty supporting itself against gravity—sufficient difficulty that only if the star’s mass were less than that of 1.4 Suns could the squeeze of gravity be counterbalanced
This meant that no white dwarf could ever have a mass exceeding 1.4 solar masses!
With his limited knowledge of astrophysics, Chandrasekhar was deeply puzzled about the meaning of this strange result. Time and again Chandrasekhar checked his calculations, but he could find no error. So, in the last few days of his voyage, he wrote two technical manuscripts for publication. In one he described his conclusions about the structure of low-mass, low-density white dwarfs such as Sirius B. In the other he explained, very briefly, his conclusion that no white dwarf can ever be heavier than 1.4 Suns.
W hen Chandrasekhar arrived in Cambridge, Fowler was out of the country. In September, when Fowler returned, Chandrasekhar eagerly went to his office and gave him the two manuscripts. Fowler approved the first one and sent it to Philosophical Magazine for publication, but the second one, the white-dwarf maximum mass, puzzled him. He could not understand Chandrasekhar’s proof that no white dwarf can be heavier than 1.4 Suns; but then, he was a physicist rather than an astronomer, so he asked his colleague, the famous astronomer E. A. Milne, to look at it. When Milne couldn’t understand the proof either, Fowler declined to send it for publication.
Chandrasekhar was annoyed. Three months had passed since his arrival in England, and Fowler had been sitting on his paper for two months. This was too long to wait for approval to publish. So, piqued, Chandrasekhar abandoned his attempts to publish in Britain and mailed the manuscript to the Astrophysical Journal in America.
After some weeks there came a response from the editor at the University of Chicago: The manuscript had been sent to the American physicist Carl Eckart for refereeing. In the manuscript Chandrasekhar stated, without explanation, the result of his relativistic and quantum mechanical calculation, that the resistance to compression is
at ultra-high densities. This
resistance was essential to the limit on how heavy a white dwarf can be. If the resistance were larger than
,
then white dwarfs could be as heavy as they wished—and Eckart thought it should be larger. Chandrasekhar fired off a reply containing a mathematical derivation of the
resistance; Eckart, reading the details, conceded that Chandrasekhar was right and approved his paper for publication. Finally, a full year after Chandrasekhar had written it, his paper got published.
4
The response of the astronomical community was deafening silence. Nobody seemed interested. So Chandrasekhar, wanting to complete his Ph.D. degree, turned to other, more acceptable research.
T
hree years later, with his Ph.D. finished, Chandrasekhar visited Russia to exchange research ideas with Soviet scientists. In Leningrad a young Armenian astrophysicist, Viktor Amazapovich Ambartsumian, told Chandrasekhar that the world’s astronomers would not believe his strange limit on the masses of white dwarfs unless he computed, from the laws of physics, the masses of a representative sample of white dwarfs and demonstrated explicitly that they were all below his claimed limit. It was not enough, Ambartsumian asserted, that Chandrasekhar had analyzed white dwarfs with rather low densities and resistances of
, and white dwarfs with extremely high densities and resistances of
; he needed also to analyze a goodly sample of white dwarfs with densities in between and show that they, too, always have masses below 1.4 Suns. Upon returning to Cambridge, Chandrasekhar took up Ambartsumian’s challenge.
One foundation that Chandrasekhar would need was the equation of state of white-dwarf matter over the entire range of densities, running from low to extremely high. (By the “state” of the matter, physicists mean the matter’s density and pressure—or equivalently its density and its resistance to compression, since from the resistance and the density one can compute the pressure. By “equation of state” is meant the relationship between the resistance and the density, that is, the resistance as a function of density.)
In late 1934, when Chandrasekhar took up Ambartsumian’s challenge, the equation of state for white-dwarf matter was known, thanks to calculations by Edmund Stoner of Leeds University in England and Wilhelm Anderson of Tartu University in Estonia. The Stoner–Anderson equation of state showed that, as the density of the white-dwarf matter is squeezed higher and higher, moving from the nonrelativistic regime of low densities and low electron speeds into the relativistic domain of extremely high densities and electron speeds near the speed of light, the matter’s resistance to compression decreases smoothly from
to
(left half of Figure 4.3). The resistance could not have behaved more simply.
To meet Ambartsumian’s challenge, Chandrasekhar had to combine this equation of state (this dependence of resistance on density) with the star’s law of balance between gravity and pressure, and thereby obtain a differential equation 5 describing the star’s internal structure—that is, describing the variation of its density with distance from the star’s center. He then had to solve that differential equation for a dozen or so stars that have central densities spanning the range from low to extremely high. Only by solving the differential equation for each star could he learn the star’s mass, and see whether it is less than 1.4 Suns.
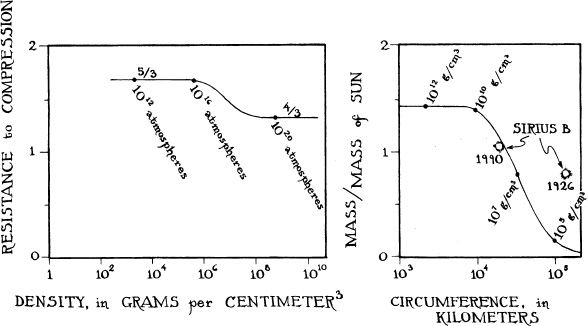
4.3 Left: The Stoner–Anderson equation of state for white-dwarf matter, that is, the relationship between the matter’s density and its resistance to compression. Plotted horizontally is the density to which the matter has been squeezed. Plotted vertically is its resistance (the percentage increase of pressure that accompanies a 1percent increase of density). Along the curve is marked the squeeze pressure (equal to internal pressure), in multiples of the pressure of the Earth’s atmosphere. Right: The circumferences (plotted horizontally) and masses (plotted vertically) of white-dwarf stars as computed by Chandrasekhar using Eddington’s Braunschweiger mechanical calculator. Along the curve is marked the density of the matter at the center of the star, in grams per cubic centimeter.
For stars with low or extremely high central density, which Chandrasekhar had studied on the steamer, he had found the solution to the differential equation and the resulting stellar structures in Eddington’sbook; but for stars with intermediate densities Eddington’s book was of no help and, despite great effort, Chandrasekhar was not able to deduce the solution using mathematical formulas. The mathematics was too complicated. There was no recourse but to solve his differential equation numerically, on a computer.
Now, the computers of 1934 were very different from those of the 1990s. They were more like the simplest of pocket calculators: They could only multiply two numbers at a time, and the user had to enter those numbers by hand, then turn a crank. The crank set into motion a complicated morass of gears and wheels which performed the multiplication and gave the answer.
Such computers were precious machines; it was very hard to gain access to one. But Arthur Eddington owned one, a “Braunschweiger” about the size of an early 1990s desk-top personal computer; so Chandrasekhar, who by now had become well acquainted with the great man, went to Eddington and asked to borrow it. Eddington at the time was embroiled in a controversy with Milne over white dwarfs and was eager to see the full details of white-dwarf structure worked out, so he let Chandrasekhar cart the Braunschweiger off to the rooms in Trinity College where Chandrasekhar was living.
The calculations were long and tedious. Each evening after dinner Eddington, who was a fellow of Trinity College, would ascend the stairs to Chandrasekhar’s rooms to see how they were coming and to give him encouragement.
At last, after many days, Chandrasekhar finished. He had met Ambartsumian’s challenge. For each of ten representative white-dwarf stars, he had computed the internal structure, and then from it the star’s total mass and its circumference. All the masses were less than 1.4 Suns, as he had firmly expected. Moreover, when he plotted the stars’ masses and circumferences on a diagram and “connected the dots,” he obtained a single, smooth curve (right half of Figure 4.3; see also Box 4.2), and the measured masses and circumferences of Sirius B and other known white dwarfs agreed with that curve moderately well. (With improved, modern astronomical observations, the fit has become much better; note the new, 1990 values of the mass and circumference of Sirius B in Figure 4.3.) Proud of his results and anticipating that the world’s astronomers would finally accept his claim that white dwarfs cannot be heavier than 1.4 Suns, Chandrasekhar was very happy.
Especially gratifying would be the opportunity to present these results to the Royal Astronomical Society in London. Chandrasekhar was scheduled for a presentation on Friday, 11 January 1935. Protocol dictated that the details of the meeting’s program be kept secret until the meeting started, but Miss Kay Williams, the assistant secretary of the Society and a friend of Chandrasekhar’s, was in the habit of sending him programs secretly in advance. On Thursday evening when the program arrived in the mail, he was surprised to discover that immediately following his own talk there would be a talk by Eddington on the subject of “Relativistic Degeneracy.” Chandrasekhar was a little annoyed. For the past few months Eddington had been coming to see him at least once a week about his work and had been reading drafts of the articles he was writing, but never once had Eddington mentioned doing any research of his own on the same subject!
Box 4.2
An Explanation of the Masses and Circumferences of White-Dwarf Stars
To understand qualitatively why white dwarfs have the masses and circumferences shown in Figure 4.3, examine the drawing below. It shows the average pressure and gravity inside a white dwarf (plotted upward) as functions of the star’s circumference (plotted rightward) or density (plotted leftward). If one compresses the star, so its density increases and its circumference decreases (leftward motion in the drawing), then the star’s pressure goes up in the manner of the solid curve, with a sharper rise at low densities where the resistance to compression is
, and a slower rise at high densities where it is
. This same compression of the star causes the star’s surface to move in toward its center, thereby increasing the strength of the star’s internal gravity in the manner of the dashed lines. The rate of gravity’s increase is analogous to a
resistance: There is a
percent increase in gravity’s strength for each 1 percent compression. The drawing shows several dashed gravity lines, one for each value of the star’s mass, because the greater the star’s mass, the stronger its gravity.
Inside each star, for example a 1.2-solar-mass star, gravity and pressure must balance each other. The star, therefore, must reside at the intersection of the dashed gravity line marked “1.2 solar masses” and the solid pressure curve; this intersection determines the star’s circumference (marked on bottom of graph). If the circumference were larger, then the star’s dashed gravity line would be above its solid pressure curve, gravity would overwhelm pressure, and the star would implode. If the circumference were smaller, pressure would overwhelm gravity, and the star would explode.
The intersections of the several dashed lines with the solid curve correspond to the masses and circumferences of equilibrium white dwarfs, as shown in the right half of Figure 4.3. For a star of small mass (lowest dashed line), the circumference at the intersection is large. For a star of higher mass (higher dashed lines), the circumference is smaller. For a star with mass above 1.4 Suns, there is no intersection whatsoever; the dashed gravity line is always above the solid pressure curve, so gravity always overwhelms pressure, no matter what the star’s circumference may be, forcing the star to implode.
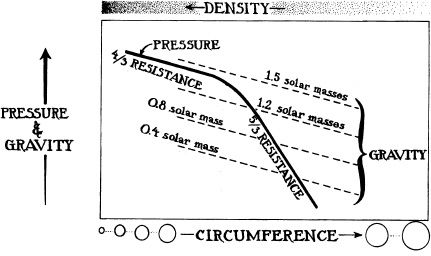
Suppressing his annoyance, Chandrasekhar went down to dinner. Eddington was there, dining at high table, but protocol dictated that, just because’ you knew so eminent a man, and just because he had been expressing an interest in your work, you did not thereby have a right to go bother him about such a matter as this. So Chandrasekhar sat down elsewhere and held his tongue.
After dinner Eddington himself sought Chandrasekhar out and said, “I’ve asked Smart to give you half an hour tomorrow instead of the customary fifteen minutes.” Chandrasekhar thanked him and waited for him to say something about his own talk, but Eddington just excused himself and left. Chandrasekhar’s annoyance acquired an anxious twinge.
The Battle
T he next morning Chandrasekhar took the train down to London and a taxi to Burlington House, the home of the Royal Astronomical Society. While he and a friend, Bill McCrea, were waiting for the meeting to start, Eddington came walking by, and McCrea, having just read the program, asked, “Well, Professor Eddington, what are we to understand by ‘Relativistic Degeneracy’?” Eddington, in reply, turned to Chandrasekhar and said, “That’s a surprise for you,” and walked off leaving Chandrasekhar even more anxious.
Left: Arthur Stanley Eddington in 1932. Right: Subrahmanyan Chandrasekhar in 1934. [Left: courtesy UPI/Bettmann; right: courtesy S. Chandrasekhar.]
At last the meeting started. Time dragged by as the Society president made various announcements, and various astronomers gave miscellaneous talks. At last it was Chandrasekhar’s turn. Suppressing his anxiety, he gave an impeccable presentation, emphasizing particularly his maximum mass for white dwarfs.
After polite applause from the fellows of the Society, the president invited Eddington to speak.
Eddington began gently, by reviewing the history of white-dwarf research. Then, gathering steam, he described the disturbing implications of Chandrasekhar’s maximum-mass result:
In Chandrasekhar’s diagram of the mass of a star plotted vertically and its circumference plotted horizontally (Figure 4.4), there is only one set of masses and circumferences for which gravity can be counterbalanced by nonthermal pressure (pressure that remains after the star turns cold): that of white dwarfs. In the region to the left of Chandrasekhar’s white-dwarf curve (shaded region; stars with smaller circumferences), the star’s nonthermal degeneracy pressure completely overwhelms gravity. The degeneracy pressure will drive any star in the shaded region to explode. In the region to the right of the white-dwarf curve (white region; stars with larger circumferences), gravity completely overwhelms the star’s degeneracy pressure. Any cold star which finds itself in this region will immediately implode under gravity’s squeeze.
The Sun can live in the white region only because it is now very hot; its thermal (heat-induced) pressure manages to counterbalance its gravity. However, when the Sun ultimately cools down, its thermal pressure will disappear and it no longer will be able to support itself. Gravity will force it to shrink smaller and smaller, squeezing the Sun’s electrons into smaller and smaller cells, until at last they protest with enough degeneracy pressure (nonthermal pressure) to halt the shrinkage. During this shrinkage “death,” the Sun’s mass will remain nearly constant, but its circumference will decrease, so it will move leftward on a horizontal line in Figure 4.4, finally stopping on the white-dwarf curve—its grave. There, as a white dwarf, the Sun will continue to reside forever, gradually cooling and becoming a black dwarf—a cold, dark, solid object about the size of the Earth but a million times heavier and denser.
This ultimate fate of the Sun seemed quite satisfactory to Eddington. Not so.the ultimate fate of a star more massive than Chandrasekhar’s white-dwarf limit of 1.4 solar masses-for example, Sirius, the 2.3-solar-mass companion of Sirius B. If Chandrasekhar were right, such a star could never die the gentle death that awaits the Sun. When the radiation it emits into space has carried away enough heat for the star to begin to cool, its thermal pressure will decline, and gravity’s squeeze will make it shrink smaller and smaller. For so massive a star as Sirius, the shrinkage cannot be halted by nonthermal degeneracy pressure. This is clear from Figure 4.4, where the shaded region does not extend high enough to intercept Sirius’s shrinking track. Eddington found this prediction disturbing.
“The star has to go on radiating and radiating and contracting and contracting,” Eddington told his audience, “until, I suppose, it gets down to a few kilometers radius, when gravity becomes strong enough to hold in the radiation, and the star can at last find peace.” (In the words of the 1990s, it must form a black hole.) “Dr. Chandrasekhar had got this result before, but he has rubbed it in in his last paper; and, when discussing it with him, I felt driven to the conclusion that this was almost a reductio ad absurdum of the relativistic degeneracy formula. Various accidents may intervene to save the star, but I want more protection than that. I think there should be a law of Nature to prevent a star from behaving in this absurd way!”
Then Eddington argued that Chandrasekhar’s mathematical proof of his result could not be trusted because it was based on an inadequately sophisticated meshing of special relativity with quantum mechanics. “I do not regard the offspring of such a union as born in lawful wedlock,” Eddington said. “1 feel satisfied myself that [if the meshing is made correctly], the relativity corrections are compensated, so that we come back to the ‘ordinary’ formula” (that is, to a
resistance, which would permit white dwarfs to be arbitrarily massive and thereby would enable pressure to halt the contraction of Sirius at the hypothetical dotted curve in Figure 4.4). Eddington then sketched how he
thought special relativity and quantum mechanics should be meshed, a rather different kind of mesh than Chandrasekhar, Stoner, and Anderson had used, and a mesh, Eddington claimed, that would save all stars from the black-hole fate.
Chandrasekhar was shocked. He had never expected such an attack on his work. Why had Eddington not discussed it with him in advance? And as for Eddington’s argument, to Chandrasekhar it looked specious—almost certainly wrong.
Now, Arthur Eddington was the great man of British astronomy. His discoveries were almost legendary. He was largely responsible for as tronomers’ understanding of normal stars like the Sun and Sirius, their interiors, their atmospheres, and the light that they emit; so, naturally, the fellows of the Society, and astronomers throughout. the world, listened with great respect. Clearly, if Eddington thought Chandrasekhar’s analysis incorrect, then it must be incorrect.
4.4 When a normal star such as the Sun or Sirius (not Sirius B) starts to cool off, it must shrink, moving leftward in this diagram of mass versus circumference. The shrinkage of the Sun will stop when it reaches the edge of the shaded region (the white-dwarf curve). There degeneracy pressure balances gravity’s squeeze. The shrinkage of Sirius, by contrast, cannot be so stopped because it never reaches the edge of the shaded region. See Box 4.2 for a different depiction of these conclusions. If, as Eddington claimed, white-dwarf matter’s resistance to compression were always 5/3, that is, if relativity did not reduce it to
at high densities, then the graph of mass versus circumference would have the form of the faint dotted curve, and the shrinkage of Sirius would stop there.
After the meeting, one fellow after another came up to Chandrasekhar to offer condolences. “I feel it in my bones that Eddington is right,” Milne told him.
T
he next day, Chandrasekhar began appealing to his physicist friends for help. To Leon Rosenfeld in ‘Copenhagen, he wrote, “If Eddington is right, my last four months’ work all goes in the fire. Could Eddington be right? I should very much like to know Bohr’s opinion.” (Niels Bohr
was one of the fathers of quantum mechanics and the most respected physicist of the 1930s.) Rosenfeld replied two days later, with assurances that he and Bohr both were convinced that Eddington was wrong and Chandrasekhar right. “I may say that your letter was some
surprise for me,” he wrote, “for nobody had ever dreamt of questioning the equations [that you used to derive the
resistance] and Eddington’s remark as reported in your letter is utterly obscure. So I think you had better cheer up and not let you scare [sic
] so much by high priests.” In a follow-up letter on the same day, Rosenfeld wrote, “Bohr and I are absolutely unable to see any meaning in Eddington’s statements.”
But for astronomers, the matter was not so clear at first. They had no expertise in these issues of quantum mechanics and relativity, so Eddington’s authority held sway amongst them for several years. Moreover, Eddington stuck to his guns. He was so blinded by his opposition to black holes that his judgment was totally clouded. He so deeply wanted there to “be a law of Nature to prevent a star from behaving in this absurd way” that he continued to believe for the rest of his life that there is such a law—when, in fact, there is none.
By the late 1930s, astronomers, having talked to their physicist colleagues, understood Eddington’s error, but their respect for his enormous earlier achievements prevented them from saying so in public. In a lecture at an astronomy conference in Paris in 1939, Eddington once again attacked Chandrasekhar’s conclusions. As Eddington attacked, Chandrasekhar passed a note to Henry Norris Russell (a famous astronomer from Princeton University in America), who was presiding. Chandrasekhar’s note asked for permission to reply. Russell passed back a note of his own saying, “I prefer you don’t,” even though earlier in the day Russell had told Chandrasekhar privately, “Out there we don’t believe in Eddington.”
With the world’s leading astronomers having finally—at least behind Eddington’s back—accepted Chandrasekhar’s maximum mass for white dwarfs, were they then ready to admit that black holes might exist in the real Universe? Not at all. If nature provided no law against them of the sort that Eddington had sought, then nature would surely find another way out: Presumably, every massive star would eject enough matter into interstellar space, as it ages or during its death throes, to reduce its mass below 1.4 Suns and thereby enter a safe, white-dwarf grave. This was the view to which most astronomers turned when Eddington lost his battle, and they adhered to it through the 1940s and 1950s, and into the early 1960s.
A s for Chandrasekhar, he was badly burned by the controversy with Eddington. As he recalled some forty years later, “I felt that astronomers without exception thought that I was wrong. They considered me as a sort of Don Quixote trying to kill Eddington. As you can imagine, it was a very discouraging experience for me—to find myself in a controversy with the leading figure of astronomy and to have my work completely and totally discredited by the astronomical community. I had to make up my mind as to what to do. Should I go on the rest of my life fighting? After all I was in my middle twenties at that time. I foresaw for myself some thirty to forty years of scientific work, and I simply did not think it was productive to constantly harp on something which was done. It was much better for me to change my field of interest and go into something else.”
So in 1939 Chandrasekhar turned his back on white dwarfs and stellar death, and did not return to them for a quarter century (Chapter 7 ).
And what of Eddington? Why did he treat Chandrasekhar so badly? To Eddington, the treatment may not have seemed bad at all. Roughand- tumble, freewheeling intellectual conflict was a way of life for him. Treating young Chandrasekhar in this manner may have been, in some sense, a measure of respect, a sign that he was accepting Chandrasekhar as a member of the astronomical establishment. In fact, from their first confrontation in 1935 until Eddington’s death in 1944, Eddington displayed warm personal affection for Chandrasekhar, and Chandrasekhar, though burned by the controversy, reciprocated.
1. For a clear discussion of the laws of quantum mechanics, see The Cosmic Code by Heinz Pagels (Simon and Schuster, 1982).
2. It is dangerously easy, in a delicate measurement, to get the result that one thinks one is supposed to get. Adams’s gravitational redshift measurement is an example. His result agreed with the predictions, but the predictions were severely wrong (five times too small) due to errors in astronomers’ estimates of the mass and circumference of Sirius B.
3. This usage of the word “degenerate” does not have its origins in the concept of “moral degeneracy” (the lowest possible level of morality), but rather in the concept of the electrons having reached their lowest possible levels of energy.
4. In the meantime, Edmund C. Stoner had independently derived and published the existence of the white-dwarf maximum mass, but his derivation was rather less convincing than Chandrasekhar’s because it pretended the star had a constant density throughout its interior.
5. A differential equation is one that combines in a single formula various functions and their rates of change, that is, the functions and their “derivatives.” In Chandrasekhar’s differential equation, the functions were the star’s density and pressure and the strength of its gravity, and they were functions of distance from the star’s center. The differential equation was a relation between these functions and the rate that they change as one moves outward through the star. By “solve the differential equation” is meant “compute the functions themselves from this differential equation.”